动态

详情

返回

實現二叉排序樹的前中後序遍歷 - 动态详情

11:55 上午 · 11月 06 ,2025

二叉排序樹定義

二叉排序樹（Binary Sort Tree），也稱為二叉查找樹（Binary Search Tree, BST）或有序二叉樹，是一種特殊的二叉樹數據結構。以下是二叉排序樹的一些核心概念：

一個二叉排序樹或者是一棵空樹，或者是具有以下性質的二叉樹：

右子樹上所有結點的值均大於它的根結點的值
左子樹上所有結點的值均小於它的根結點的值
左右子樹也分別為二叉排序樹
不存在鍵值相等的節點

代碼實現

#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>

typedef int DataType_t; 
typedef struct BSTreeNode
{
	DataType_t 			Keyval; 
	struct BSTreeNode *lchild;
	struct BSTreeNode *rchild;

}BSTNode_t;


 BSTNode_t* BSTree_Create(DataType_t KeyVal)
{
	BSTNode_t *root = (BSTNode_t *)calloc(1,sizeof(BSTNode_t));
	if(root == NULL){
		perror("Calloc memory for the root is failed!\n");
		exit(-1);
	}
	root->lchild = NULL;
	root->rchild = NULL;
	root->Keyval = KeyVal;
	return root;
}


BSTNode_t* BSTree_NewNode(DataType_t KeyVal)
{
	BSTNode_t *New = (BSTNode_t *)calloc(1,sizeof(BSTNode_t));
	if(New == NULL){
		perror("Calloc memory for the New is failed!\n");
		return NULL;
	}
	New->lchild = NULL;
	New->rchild = NULL;
	New->Keyval   = KeyVal;
	return New;
}


bool BSTree_InsertNode(BSTNode_t* root, DataType_t KeyVal)
{
    if (root == NULL) {
        printf("Error: root is NULL, cannot insert %d\n", KeyVal);
        return false;
    }

    BSTNode_t *New = BSTree_NewNode(KeyVal);
    if (New == NULL) {
        printf("Create NewNode Error\n");
        return false;
    }

    BSTNode_t *Proot = root;
    while (Proot != NULL) {
        if (KeyVal == Proot->Keyval) {
            printf("Can not Insert, duplicate value: %d\n", KeyVal);
            free(New); // 避免內存泄漏
            return false;
        }
        else if (KeyVal < Proot->Keyval) {
            if (Proot->lchild == NULL) {
                Proot->lchild = New;
                return true;
            }
            Proot = Proot->lchild;
        }
        else {
            if (Proot->rchild == NULL) {
                Proot->rchild = New;
                return true;
            }
            Proot = Proot->rchild; // 
        }
    }

    return true; //
}

//前序遍歷
bool BSTree_PreOrder(BSTNode_t* root)
{
	if(root == NULL)
	{
		return false;
	}

	printf("KeyVal = %d\n",root->Keyval);
	BSTree_PreOrder(root->lchild);
	BSTree_PreOrder(root->rchild);

	return true;
}
//中序遍歷
bool BSTree_InOrder(BSTNode_t* root)
{
	if(root == NULL)
	{
		return false;
	}
	BSTree_InOrder(root->lchild);
	printf("KeyVal = %d\n",root->Keyval);
	BSTree_InOrder(root->rchild);
	return true;
}
//後序遍歷
bool BSTree_PostOrder(BSTNode_t* root)
{
	if(root == NULL)
	{
		return false;
	}
	BSTree_PostOrder(root->lchild);
	BSTree_PostOrder(root->rchild);
	printf("KeyVal = %d\n",root->Keyval);
	return true;
}

int main()
{
    // --- 1. 測試：創建根節點 ---
    printf("1. 創建根節點...\n");
    BSTNode_t* root = BSTree_Create(50);
    if (root) {
        printf("成功創建根節點，值為: %d\n", root->Keyval);
    }

    // --- 2. 測試：插入多個節點 ---
    printf("\n2. 插入其他節點...\n");
    int values[] = {30, 70, 20, 40, 60, 80, 35, 45};
    int n = sizeof(values) / sizeof(values[0]);

    for (int i = 0; i < n; i++) {
        if (BSTree_InsertNode(root, values[i])) {
            printf("成功插入: %d\n", values[i]);
        }
    }
    // --- 3. 測試：重複插入（應失敗）---
    printf("\n3. 測試重複插入...\n");
    BSTree_InsertNode(root, 40);  // 已存在
    BSTree_InsertNode(root, 50);  // 根節點已存在

    // --- 4. 測試：遍歷操作 ---
    printf("\n4. 遍歷測試...\n");

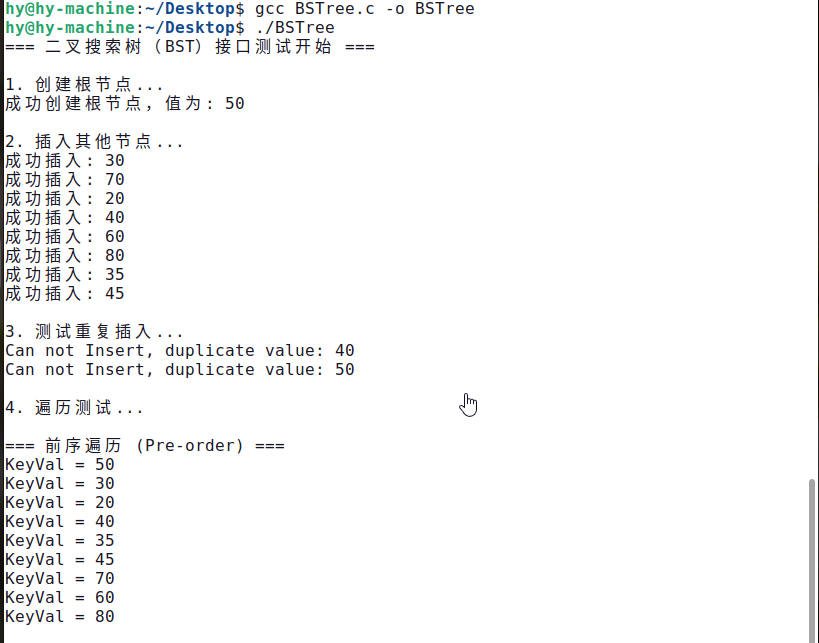
    printf("\n=== 前序遍歷 (Pre-order) ===\n");
    BSTree_PreOrder(root);

    printf("\n=== 中序遍歷 (In-order) - 應升序輸出 ===\n");
    BSTree_InOrder(root);

    printf("\n=== 後序遍歷 (Post-order) ===\n");
    BSTree_PostOrder(root);

 	printf("\n7. 測試插入到 NULL 樹（應失敗）...\n");
    BSTNode_t* emptyTree = NULL;
    bool result = BSTree_InsertNode(emptyTree, 100);
    if (!result) {
        printf("正確：無法向 NULL 樹插入節點。\n");
    }
    printf("\n所有測試完成\n");
    return 0;
}