大家好,我是半夏之沫 😁😁 一名金融科技領域的JAVA系統研發😊😊
我希望將自己工作和學習中的經驗以最樸實,最嚴謹的方式分享給大家,共同進步👉💓👈
👉👉👉👉👉👉👉👉💓寫作不易,期待大家的關注和點贊💓👈👈👈👈👈👈👈👈
👉👉👉👉👉👉👉👉💓關注微信公眾號【技術探界】 💓👈👈👈👈👈👈👈👈
前言
跳錶可以達到和紅黑樹一樣的時間複雜度O(logN),且實現簡單,Redis中的有序集合對象的底層數據結構就使用了跳錶。本篇文章將對跳錶的實現進行學習。
正文
一. 跳錶的基礎概念
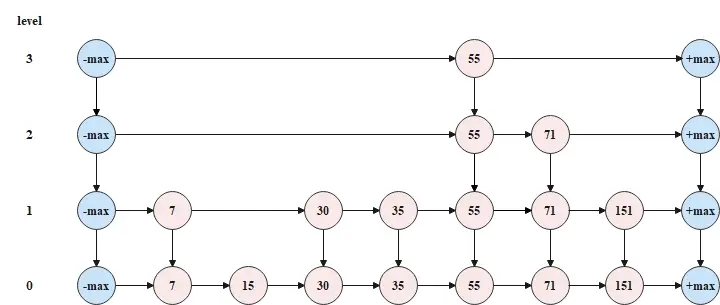
跳錶,即跳躍表(Skip List),是基於並聯的鏈表數據結構,操作效率可以達到O(logN),對併發友好,跳錶的示意圖如下所示。
跳錶的特點,可以概括如下。
- 跳錶是多層(level)鏈表結構;
- 跳錶中的每一層都是一個有序鏈表,並且按照元素升序(默認)排列;
- 跳錶中的元素會在哪一層出現是隨機決定的,但是隻要元素出現在了第k層,那麼k層以下的鏈表也會出現這個元素;
- 跳錶的底層的鏈表包含所有元素;
- 跳錶頭節點和尾節點不存儲元素,且頭節點和尾節點的層數就是跳錶的最大層數;
- 跳錶中的節點包含兩個指針,一個指針指向同層鏈表的後一節點,一個指針指向下層鏈表的同元素節點。
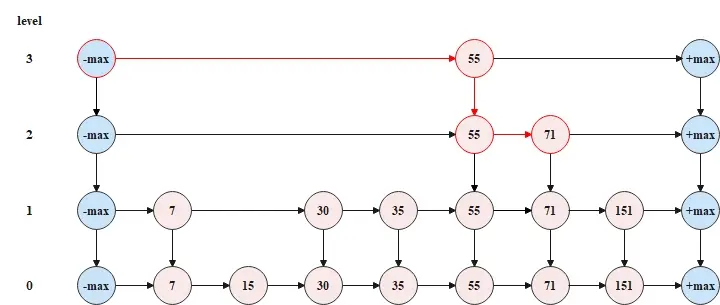
以上圖中的跳錶為例,如果要查找元素71,那麼查找流程如下圖所示。
從頂層鏈表的頭節點開始查找,查找到元素71的節點時,一共遍歷了4個節點,但是如果按照傳統鏈表的方式(即從跳錶的底層鏈表的頭節點開始向後查找),那麼就需要遍歷7個節點,所以跳錶以空間換時間,縮短了操作跳錶所需要花費的時間。
二. 跳錶的節點
已知跳錶中的節點,需要有指向當前層鏈表後一節點的指針,和指向下層鏈表的同元素節點的指針,所以跳錶中的節點,定義如下。
public class SkiplistNode {
public int data;
public SkiplistNode next;
public SkiplistNode down;
public int level;
public SkiplistNode(int data, int level) {
this.data = data;
this.level = level;
}
}上述是跳錶中的節點的最簡單的定義方式,存儲的元素data為整數,節點之間進行比較時直接比較元素data的大小。
三. 跳錶的初始化
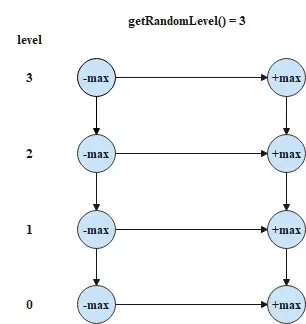
跳錶初始化時,將每一層鏈表的頭尾節點創建出來並使用集合將頭尾節點進行存儲,頭尾節點的層數隨機指定,且頭尾節點的層數就代表當前跳錶的層數。初始化後,跳錶結構如下所示。
跳錶初始化的相關代碼如下所示。
public LinkedList<SkiplistNode> headNodes;
public LinkedList<SkiplistNode> tailNodes;
public int curLevel;
public Random random;
public Skiplist() {
random = new Random();
// headNodes用於存儲每一層的頭節點
headNodes = new LinkedList<>();
// tailNodes用於存儲每一層的尾節點
tailNodes = new LinkedList<>();
// 初始化跳錶時,跳錶的層數隨機指定
curLevel = getRandomLevel();
// 指定了跳錶的初始的隨機層數後,就需要將每一層的頭節點和尾節點創建出來並構建好關係
SkiplistNode head = new SkiplistNode(Integer.MIN_VALUE, 0);
SkiplistNode tail = new SkiplistNode(Integer.MAX_VALUE, 0);
for (int i = 0; i <= curLevel; i++) {
head.next = tail;
headNodes.addFirst(head);
tailNodes.addFirst(tail);
SkiplistNode headNew = new SkiplistNode(Integer.MIN_VALUE, head.level + 1);
SkiplistNode tailNew = new SkiplistNode(Integer.MAX_VALUE, tail.level + 1);
headNew.down = head;
tailNew.down = tail;
head = headNew;
tail = tailNew;
}
}四. 跳錶的添加方法
每一個元素添加到跳錶中時,首先需要隨機指定這個元素在跳錶中的層數,如果隨機指定的層數大於了跳錶的層數,則在將元素添加到跳錶中之前,還需要擴大跳錶的層數,而擴大跳錶的層數就是將頭尾節點的層數擴大。下面給出需要擴大跳錶層數的一次添加的過程。
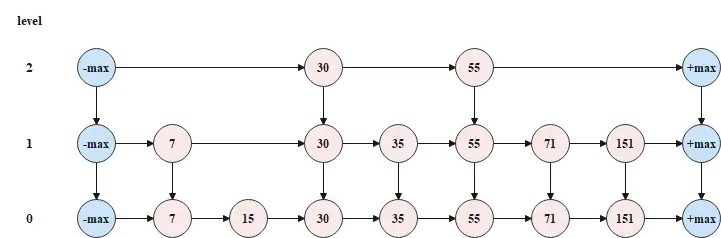
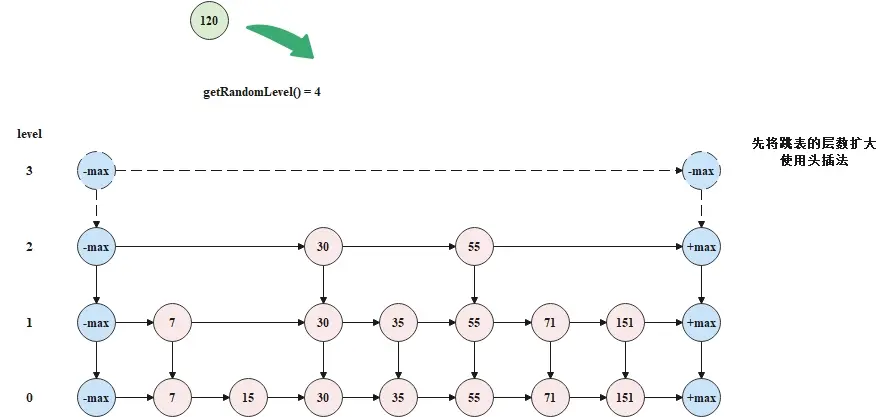
初始狀態時,跳錶的層數為2,如下圖所示。
現在要往跳錶中添加元素120,並且隨機指定的層數為3,大於了當前跳錶的層數2,此時需要先擴大跳錶的層數,如下圖所示。
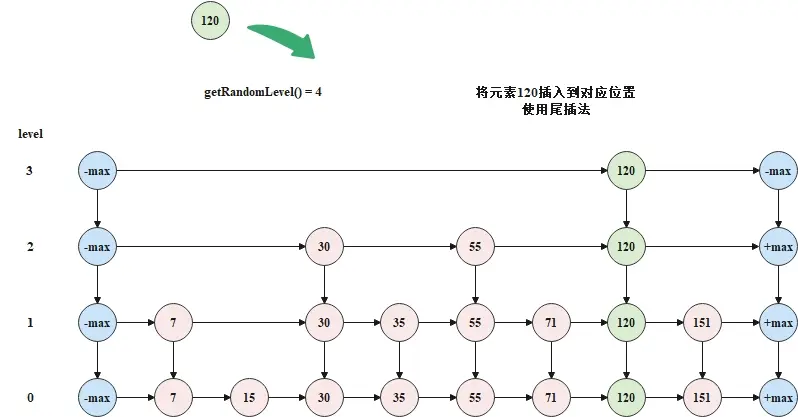
將元素120插入到跳錶中時,從頂層開始,逐層向下插入,如下圖所示。
跳錶的添加方法的代碼如下所示。
public void add(int num) {
// 獲取本次添加的值的層數
int level = getRandomLevel();
// 如果本次添加的值的層數大於當前跳錶的層數
// 則需要在添加當前值前先將跳錶層數擴充
if (level > curLevel) {
expanLevel(level - curLevel);
}
// curNode表示num值在當前層對應的節點
SkiplistNode curNode = new SkiplistNode(num, level);
// preNode表示curNode在當前層的前一個節點
SkiplistNode preNode = headNodes.get(curLevel - level);
for (int i = 0; i <= level; i++) {
// 從當前層的head節點開始向後遍歷,直到找到一個preNode
// 使得preNode.data < num <= preNode.next.data
while (preNode.next.data < num) {
preNode = preNode.next;
}
// 將curNode插入到preNode和preNode.next中間
curNode.next = preNode.next;
preNode.next = curNode;
// 如果當前並不是0層,則繼續向下層添加節點
if (curNode.level > 0) {
SkiplistNode downNode = new SkiplistNode(num, curNode.level - 1);
// curNode指向下一層的節點
curNode.down = downNode;
// curNode向下移動一層
curNode = downNode;
}
// preNode向下移動一層
preNode = preNode.down;
}
}
private void expanLevel(int expanCount) {
SkiplistNode head = headNodes.getFirst();
SkiplistNode tail = tailNodes.getFirst();
for (int i = 0; i < expanCount; i++) {
SkiplistNode headNew = new SkiplistNode(Integer.MIN_VALUE, head.level + 1);
SkiplistNode tailNew = new SkiplistNode(Integer.MAX_VALUE, tail.level + 1);
headNew.down = head;
tailNew.down = tail;
head = headNew;
tail = tailNew;
headNodes.addFirst(head);
tailNodes.addFirst(tail);
}
}五. 跳錶的搜索方法
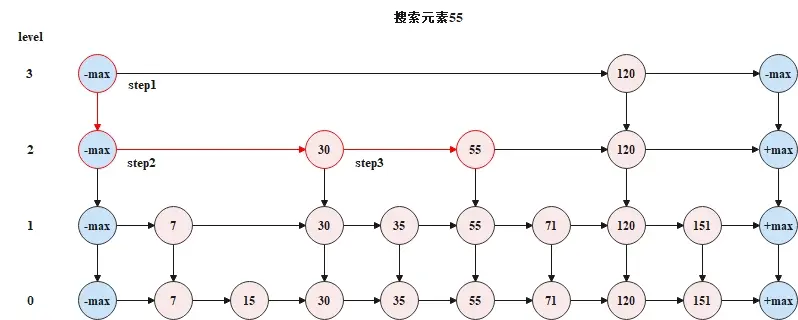
在跳錶中搜索一個元素時,需要從頂層開始,逐層向下搜索。搜索時遵循如下規則。
- 目標值大於當前節點的後一節點值時,繼續在本層鏈表上向後搜索;
- 目標值大於當前節點值,小於當前節點的後一節點值時,向下移動一層,從下層鏈表的同節點位置向後搜索;
- 目標值等於當前節點值,搜索結束。
下圖是一個搜索過程的示意圖。
跳錶的搜索的代碼如下所示。
public boolean search(int target) {
// 從頂層開始尋找,curNode表示當前遍歷到的節點
SkiplistNode curNode = headNodes.getFirst();
while (curNode != null) {
if (curNode.next.data == target) {
// 找到了目標值對應的節點,此時返回true
return true;
} else if (curNode.next.data > target) {
// curNode的後一節點值大於target
// 説明目標節點在curNode和curNode.next之間
// 此時需要向下層尋找
curNode = curNode.down;
} else {
// curNode的後一節點值小於target
// 説明目標節點在curNode的後一節點的後面
// 此時在本層繼續向後尋找
curNode = curNode.next;
}
}
return false;
}六. 跳錶的刪除方法
當在跳錶中需要刪除某一個元素時,則需要將這個元素在所有層的節點都刪除,具體的刪除規則如下所示。
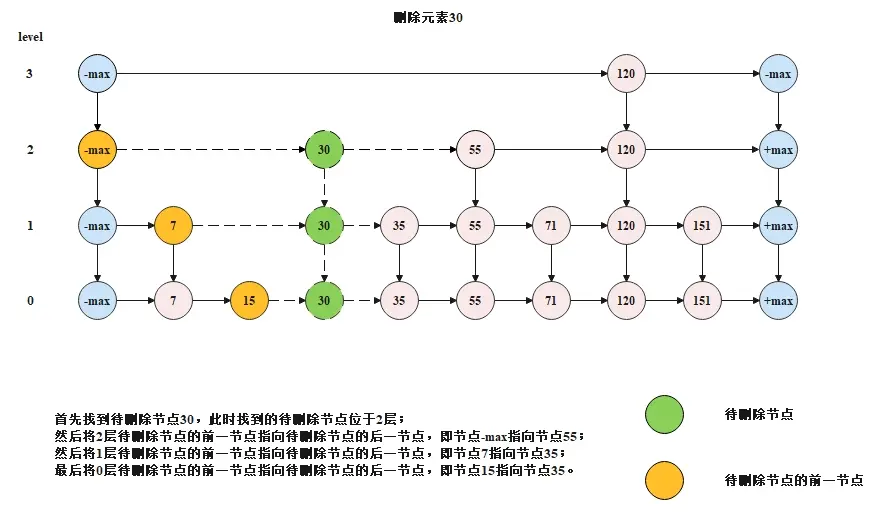
- 首先按照跳錶的搜索的方式,搜索待刪除節點,如果能夠搜索到,此時搜索到的待刪除節點位於該節點層數的最高層;
- 從待刪除節點的最高層往下,將每一層的待刪除節點都刪除掉,刪除方式就是讓待刪除節點的前一節點直接指向待刪除節點的後一節點。
下圖是一個刪除過程的示意圖。
跳錶的刪除的代碼如下所示。
public boolean erase(int num) {
// 刪除節點的遍歷過程與尋找節點的遍歷過程是相同的
// 不過在刪除節點時如果找到目標節點,則需要執行節點刪除的操作
SkiplistNode curNode = headNodes.getFirst();
while (curNode != null) {
if (curNode.next.data == num) {
// preDeleteNode表示待刪除節點的前一節點
SkiplistNode preDeleteNode = curNode;
while (true) {
// 刪除當前層的待刪除節點,就是讓待刪除節點的前一節點指向待刪除節點的後一節點
preDeleteNode.next = curNode.next.next;
// 當前層刪除完後,需要繼續刪除下一層的待刪除節點
// 這裏讓preDeleteNode向下移動一層
// 向下移動一層後,preDeleteNode就不一定是待刪除節點的前一節點了
preDeleteNode = preDeleteNode.down;
// 如果preDeleteNode為null,説明已經將底層的待刪除節點刪除了
// 此時就結束刪除流程,並返回true
if (preDeleteNode == null) {
return true;
}
// preDeleteNode向下移動一層後,需要繼續從當前位置向後遍歷
// 直到找到一個preDeleteNode,使得preDeleteNode.next的值等於目標值
// 此時preDeleteNode就又變成了待刪除節點的前一節點
while (preDeleteNode.next.data != num) {
preDeleteNode = preDeleteNode.next;
}
}
} else if (curNode.next.data > num) {
curNode = curNode.down;
} else {
curNode = curNode.next;
}
}
return false;
}七. 跳錶完整代碼
跳錶完整代碼如下所示。
public class Skiplist {
public LinkedList<SkiplistNode> headNodes;
public LinkedList<SkiplistNode> tailNodes;
public int curLevel;
public Random random;
public Skiplist() {
random = new Random();
// headNodes用於存儲每一層的頭節點
headNodes = new LinkedList<>();
// tailNodes用於存儲每一層的尾節點
tailNodes = new LinkedList<>();
// 初始化跳錶時,跳錶的層數隨機指定
curLevel = getRandomLevel();
// 指定了跳錶的初始的隨機層數後,就需要將每一層的頭節點和尾節點創建出來並構建好關係
SkiplistNode head = new SkiplistNode(Integer.MIN_VALUE, 0);
SkiplistNode tail = new SkiplistNode(Integer.MAX_VALUE, 0);
for (int i = 0; i <= curLevel; i++) {
head.next = tail;
headNodes.addFirst(head);
tailNodes.addFirst(tail);
SkiplistNode headNew = new SkiplistNode(Integer.MIN_VALUE, head.level + 1);
SkiplistNode tailNew = new SkiplistNode(Integer.MAX_VALUE, tail.level + 1);
headNew.down = head;
tailNew.down = tail;
head = headNew;
tail = tailNew;
}
}
public boolean search(int target) {
// 從頂層開始尋找,curNode表示當前遍歷到的節點
SkiplistNode curNode = headNodes.getFirst();
while (curNode != null) {
if (curNode.next.data == target) {
// 找到了目標值對應的節點,此時返回true
return true;
} else if (curNode.next.data > target) {
// curNode的後一節點值大於target
// 説明目標節點在curNode和curNode.next之間
// 此時需要向下層尋找
curNode = curNode.down;
} else {
// curNode的後一節點值小於target
// 説明目標節點在curNode的後一節點的後面
// 此時在本層繼續向後尋找
curNode = curNode.next;
}
}
return false;
}
public void add(int num) {
// 獲取本次添加的值的層數
int level = getRandomLevel();
// 如果本次添加的值的層數大於當前跳錶的層數
// 則需要在添加當前值前先將跳錶層數擴充
if (level > curLevel) {
expanLevel(level - curLevel);
}
// curNode表示num值在當前層對應的節點
SkiplistNode curNode = new SkiplistNode(num, level);
// preNode表示curNode在當前層的前一個節點
SkiplistNode preNode = headNodes.get(curLevel - level);
for (int i = 0; i <= level; i++) {
// 從當前層的head節點開始向後遍歷,直到找到一個preNode
// 使得preNode.data < num <= preNode.next.data
while (preNode.next.data < num) {
preNode = preNode.next;
}
// 將curNode插入到preNode和preNode.next中間
curNode.next = preNode.next;
preNode.next = curNode;
// 如果當前並不是0層,則繼續向下層添加節點
if (curNode.level > 0) {
SkiplistNode downNode = new SkiplistNode(num, curNode.level - 1);
// curNode指向下一層的節點
curNode.down = downNode;
// curNode向下移動一層
curNode = downNode;
}
// preNode向下移動一層
preNode = preNode.down;
}
}
public boolean erase(int num) {
// 刪除節點的遍歷過程與尋找節點的遍歷過程是相同的
// 不過在刪除節點時如果找到目標節點,則需要執行節點刪除的操作
SkiplistNode curNode = headNodes.getFirst();
while (curNode != null) {
if (curNode.next.data == num) {
// preDeleteNode表示待刪除節點的前一節點
SkiplistNode preDeleteNode = curNode;
while (true) {
// 刪除當前層的待刪除節點,就是讓待刪除節點的前一節點指向待刪除節點的後一節點
preDeleteNode.next = curNode.next.next;
// 當前層刪除完後,需要繼續刪除下一層的待刪除節點
// 這裏讓preDeleteNode向下移動一層
// 向下移動一層後,preDeleteNode就不一定是待刪除節點的前一節點了
preDeleteNode = preDeleteNode.down;
// 如果preDeleteNode為null,説明已經將底層的待刪除節點刪除了
// 此時就結束刪除流程,並返回true
if (preDeleteNode == null) {
return true;
}
// preDeleteNode向下移動一層後,需要繼續從當前位置向後遍歷
// 直到找到一個preDeleteNode,使得preDeleteNode.next的值等於目標值
// 此時preDeleteNode就又變成了待刪除節點的前一節點
while (preDeleteNode.next.data != num) {
preDeleteNode = preDeleteNode.next;
}
}
} else if (curNode.next.data > num) {
curNode = curNode.down;
} else {
curNode = curNode.next;
}
}
return false;
}
private void expanLevel(int expanCount) {
SkiplistNode head = headNodes.getFirst();
SkiplistNode tail = tailNodes.getFirst();
for (int i = 0; i < expanCount; i++) {
SkiplistNode headNew = new SkiplistNode(Integer.MIN_VALUE, head.level + 1);
SkiplistNode tailNew = new SkiplistNode(Integer.MAX_VALUE, tail.level + 1);
headNew.down = head;
tailNew.down = tail;
head = headNew;
tail = tailNew;
headNodes.addFirst(head);
tailNodes.addFirst(tail);
}
}
private int getRandomLevel() {
int level = 0;
while (random.nextInt(2) > 1) {
level++;
}
return level;
}
}總結
跳錶的時間複雜度與AVL樹和紅黑樹相同,可以達到O(logN),但是AVL樹要維持高度的平衡,紅黑樹要維持高度的近似平衡,這都會導致插入或者刪除節點時的一些時間開銷,所以跳錶相較於AVL樹和紅黑樹來説,省去了維持高度的平衡的時間開銷,但是相應的也付出了更多的空間來存儲多個層的節點,所以跳錶是用空間換時間的數據結構。
大家好,我是半夏之沫 😁😁 一名金融科技領域的JAVA系統研發😊😊
我希望將自己工作和學習中的經驗以最樸實,最嚴謹的方式分享給大家,共同進步👉💓👈
👉👉👉👉👉👉👉👉💓寫作不易,期待大家的關注和點贊💓👈👈👈👈👈👈👈👈
👉👉👉👉👉👉👉👉💓關注微信公眾號【技術探界】 💓👈👈👈👈👈👈👈👈