回憶起HashMap
概述HashMap
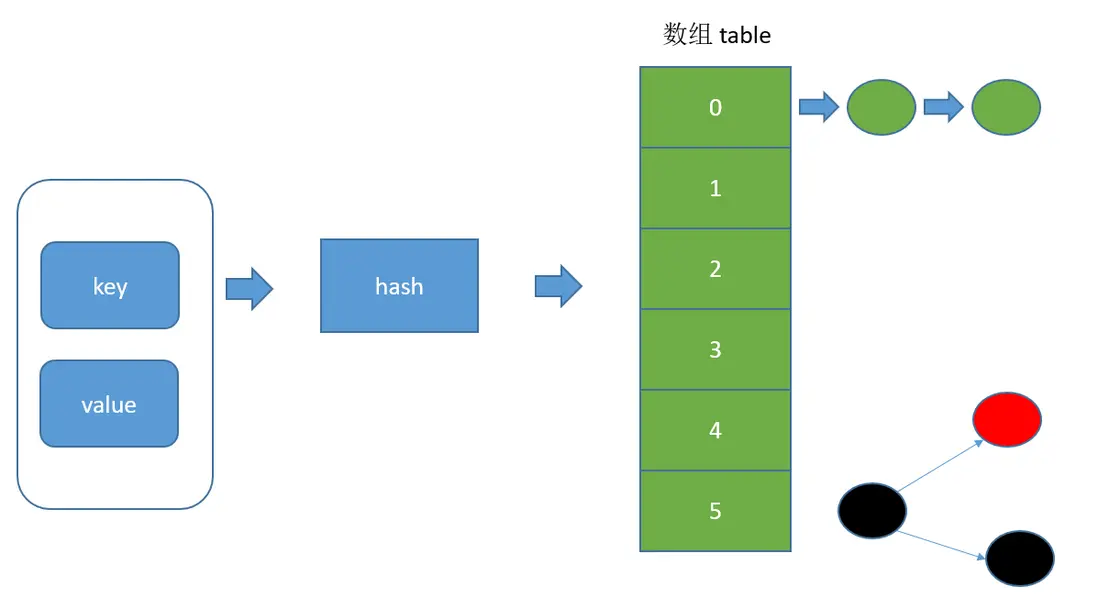
説到HashMap我腦中復現出下面這一個圖:
也就是hash算法、數組、鏈表、紅黑樹,我放入的key-value,根據hash算法會計算出來應該放置到數組的哪個位置上,如果出現了hash衝突,也就是hash算法映射出來的下標是一個,但是使用equals方法判斷不相等,那麼也就是出現了hash衝突,就會數組對應的位置形成鏈表,鏈表大於8個之後,轉為紅黑樹。為什麼是8才就轉為紅黑樹呢? 這依賴於負載因子0.75,那什麼是負載因子呢? 我們知道HashMap是一個動態容器,也就是説容器裏面放不下之後,就會自動擴大容器的大小,那HashMap在什麼時候擴容呢?
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
// 為空就初始化一次
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null) // 語句一
tab[i] = newNode(hash, key, value, null); // 語句二
else {
Node<K,V> e; K k;
if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) // 語句三
e = p;
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); // 語句四
else {
// 語句塊六
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
// 語句塊七
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
// 語句塊八
++modCount;
// 語句塊九
if (++size > threshold)
resize();
// 語句塊十
afterNodeInsertion(evict);
return null;
}這一段的邏輯為,如果數組為空,執行擴容,擴容完成,將hash的位置和n-1做與運算,得到插入的數組索引i。 這讓我想起了,這讓我想起了求餘算法, 對正整數取M取餘,餘數的範圍是0到M-1。
那用取餘算法當做hash算法? 那肯定有很多hash衝突, 我們可以隨手舉一個例子,假設數組長度是10, 我們放入的是key是17、27、37、47。這些都會放在數組索引7的這個位置上,hash衝突比較嚴重,下面是HashMap的hash方法源碼:
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}HashMap中我們一般常用String當做key的類型,我們看下String的hash算法:
public int hashCode() {
int h = hash;
if (h == 0 && value.length > 0) {
char val[] = value;
for (int i = 0; i < value.length; i++) {
h = 31 * h + val[i];
}
hash = h;
}
return h;
}也就是是用這個公式做計算: s[0]31^(n-1) + s[1]31^(n-2) + ... + s[n-1], s[i] 是第字符串中第i個字符。那我們自然會提出一個問題,這個算法的好處在哪裏呢? 為什麼是31呢? 帶着這個問題我找到了StackOverFlow,排名第一的答案是這麼回答的:
According to Joshua Bloch's Effective Java, Second Edition (a book that can't be recommended enough, and which I bought thanks to continual mentions on Stack Overflow):
根據Joshua Bloch的《Effective Java》第二版( 這本書怎麼推薦都不為過,多虧了StackOverFlow的推薦,我才買了這本書。)
The value 31 was chosen because it is an odd prime. If it were even and the multiplication overflowed, information would be lost, as multiplication by 2 is equivalent to shifting.
31被選擇是因為這是一個奇素數,如果是偶數乘法會溢出,信息會被丟失,乘以2和移位相同。
The advantage of using a prime is less clear, but it is traditional. A nice property of 31 is that the multiplication can be replaced by a shift and a subtraction for better performance: 31 * i == (i << 5) - i.
使用質數的優勢不太明顯,但是這是傳統的做法。 31有一個很好的特性是乘法可以用移位和減法代替: 31 * i == (i << 5 ) - i。
我的看法是所謂傳統的做法就是一直以來就是這麼做的,所以可能就是慣例,有那麼一絲原因。
Modern VMs do this sort of optimization automatically.(from Chapter 3, Item 9: Always override hashCode when you override equals, page 48)
現代虛擬機會自動做這類優化( 第三章,第9頁: 當你重寫equals方法時候總要重寫equals方法)。
我的想法奇素數這個概念很怪,奇數的定義是不能被2整除的數是奇數,素數的定位是指在大於1的自然數中,除了1和該數自身外,無法被其他自然數整除的數。所以除了2,所有的素數都是奇數。
來自google開源算法
在google的一個開源庫用質數1000003來計算哈希值,對應的哈希算法如下:
public int hashCode() {
int h = 1;
h *= 1000003;
h ^= this.firstName.hashCode();
h *= 1000003;
h ^= this.lastName.hashCode();
h *= 1000003;
h ^= this.age;
return h;
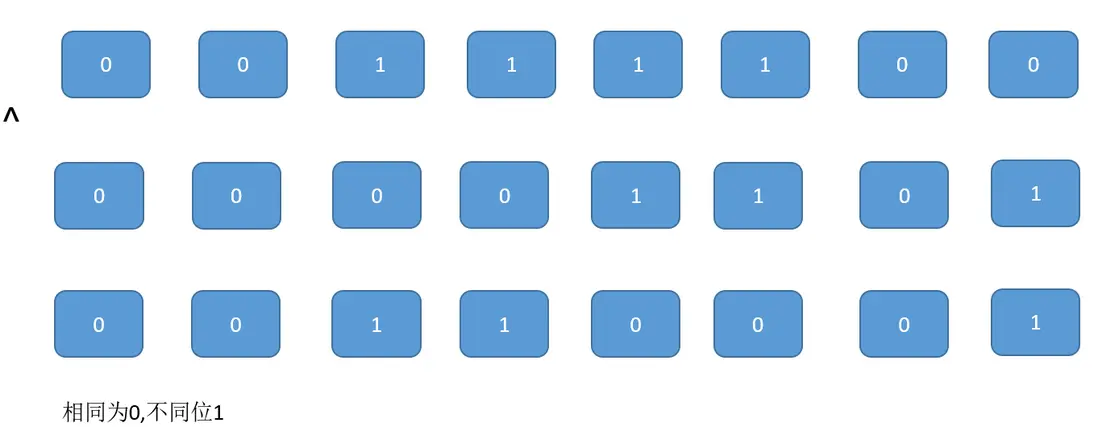
}^ 是按位異或 (XOR) 運算符,如果相對應位值相同,則結果為0,否則為1。
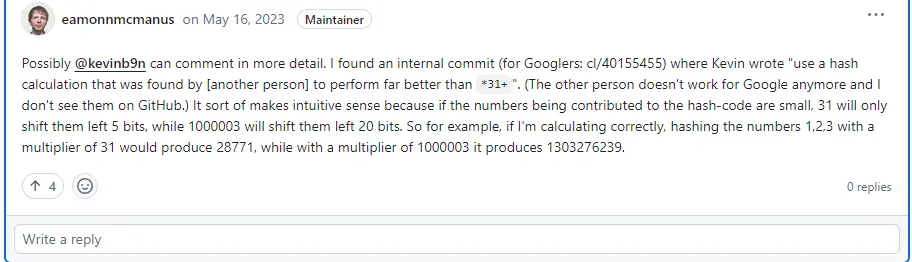
然後在這個倉庫下面我找到了一個這樣的評論:
我翻譯了一下:
也許kevinb9n可以提供更多細節,我在內部找到了一個提交。Kevin在其中寫道: "使用另一個人發現的hash算法,其性能遠遠優於*31+"(這個人已經不在google工作了,我也沒在Github上看到他)。因為如果貢獻給哈希代碼的數字很小,31只會將它們向左移動5位,而1000003則會將它們向左移動20位。
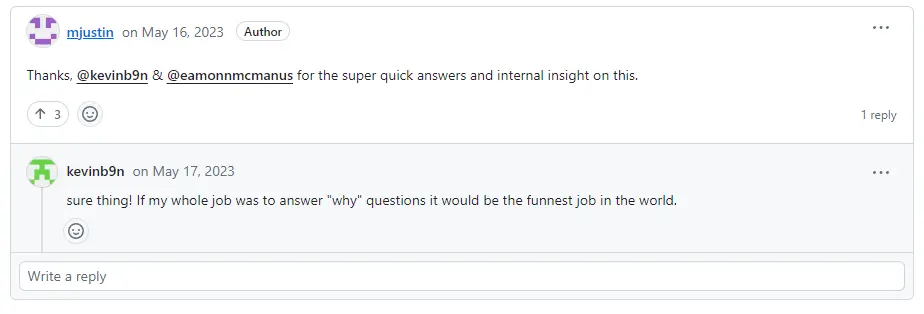
然後kevinb9n也出來了,評論如下:
Although I don't remember the details.... it is kind of exactly like me to shift things over a golden-ratio fraction of the way.
我已經記不起太多細節了,但我傾向於將東西移動到黃金分割率的幾分之一的位置上。
Though that might argue for a multiplier of 898,459, so I guess I also thought it should be a nice simple number to the human eye.
雖然這可能會讓人認為乘數是898459,但我想我也認為這對人眼來説應該是一個漂亮而簡單的數字。
黃金比例是無理數,近似值為1.6180339,一個牽強的解釋是, 1000003 除以1.618 = 618048。 這裏是個人傾向,倒是沒有太多嚴格證明在裏面。我們接着看:
But yeah, the idea of making it bigger was just to eat up all those initial zeros more quickly and get the bits to come back around and interfere with each other.
不過,是的,把它變大的想法只是為了更快地吃掉所有的初始0,並讓這些比特位回到周圍並相互干擾。
我們舉個例子來解釋一下,乘以一個較大的素數能更快地吃掉所有初始0:
-
如果我們選擇的乘數是3,這是一個質數,然後我們看兩個數高位的還是四個0,
- 0000 1001 * 3 = 0000 0011
- 0000 1010 * 3 = 0000 0030
-
現在我們來選擇乘數是1000003,來看下乘了之後的結果:
- 0000 1001 * 1000003 = 1001 0011 0011
- 0000 1010 * 1000003 = 1010 0030 0030
現在高位的0就被吃掉了,兩個數不同的地方就更多了。言下之意也就是説,31這個性能不佳,可能只是一個魔法數,這可能是一個慣例。在這個issue下面我還看到了一些温情的評論:
mjiustin回覆感謝你細緻而快速的回答。然後kevinb9n的回答是: 當然,如果我的工作全部都是在為別人解答問題,那麼這將是世上最有趣的工作。
到這裏小小總結一下
工程上一般用的比較多的也就是多項式Hash算法, 良好的hash算法映射出來的值,各個位置之上的0和1應當儘量不同。31可能就是一個傳統的值。
接着聊HashMap的hash算法
上面的註釋是:
Computes key.hashCode() and spreads (XORs) higher bits of hash to lower.
計算key 的hashCode,並通過異或操作將hash值的高位擴散到低位。
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}int是4字節,也就是32位二進制數,\>>> 是右移位運算法,這個移位該怎麼理解呢? 運算規則其實很簡單,丟棄右邊指定位數,左邊補0。
讀懂這段代碼之後,我們就可以來思考這段代碼中異或的價值所在, int的範圍是-2147483648到2147483648,前後加起來有10億的映射空間,如果hash函數映射得比較均勻鬆散,一般碰撞的概率並不大。
但我們並不能一開始就new 這麼大數組,內存也放不下,所以我們就要對數組進行取模操作,但是我們在HashMap中看到算數組索引的時候用的是與操作:
if ((p = tab[i = (n - 1) & hash]) == null)這難道是説&操作和%操作等價? 當然不是:
那我現在就想構造一個問題,對x ,y 屬於正整數,z = x & y ,z 屬於[0, y - 1] , 這個區間,我們可以嚴格推導,我們也可以給出一個反例,來印證我們的説明,現在我們首先使用嚴格推導,我們知道與運算是相同為1,不同為0,某一位被置0,其實得出的結果是在減小的,現在我們將整數集切割為偶數和奇數,我們可以用這樣的二分法來對整數集合進行分類,對於整數偶數來説末位一定是0,對於奇數來説末位一定是1,我們有兩種思路來證明這個命題,一種是從十進制轉二進制的算法去證明, 一種樸素的從十進制轉二進制的一個做法是除2取餘逆序排列, 因此我們可以做如下證明,對x = 2n ,(n= 1, 2, 3....), 2n / 2餘0, 於是末位一定是0。對x = 2n + 1 , 2n+1 , 餘數為1。 於是得到證明,
現在讓我們設y = 2n, 也就是偶數,對於x屬於整數,如果x是奇數,則末位為1,如果x大於y,高位相同的不變,低位不同的會被置0,或者我們舉一個例子,二進制數11100,也就是十進制數28,28對12進行&運算,然後得到12,所以至少是偶數,&預算是不等價於%運算的,那麼我們將目光轉向奇數,也就是將命題變為對於x屬於正整數,y是奇數,z = x & y,則求證z屬於[0, y - 1] 這個區間,於是分三種情況討論:
- x = y 如果x = y, 則 z = x = y。
第一種情況討論了之後,也沒有落到[0, y - 1] 這個區間裏面, 是不是哪裏考慮的有問題,如果數組大小是y,那麼最大下標是y - 1也沒什麼問題。 所以我們重新調整一下這個問題,對於數y,取z = x & y - 1,則z ∈ [0, y-1], 這個區間,考慮實際情況,在Java裏面數組下標從0開始,因此暗含條件為 y - 1 > 0, 因此是一個正整數,於是我們將問題調整為,對於x,y ∈正整數,z = x & y , 則z ∈ [0, y] 這個區間,但是我覺得對於y是偶數的時候,x & y 並不好,我們取x = 1 , 2 ,3, 然後會發現全部落在了0位置上,於是將目光看下了奇數,問題變形為對於x∈正整數,y= 2n + 1(n = 1,2,3,4...),對於z = x & y, c = x % y, 求證z恆等於c,這無疑對命題提出了更高的要求,我們先推導對於c = x % y,對於y = 2n + 1 , 然後c的取值區間為[0,2n] 。
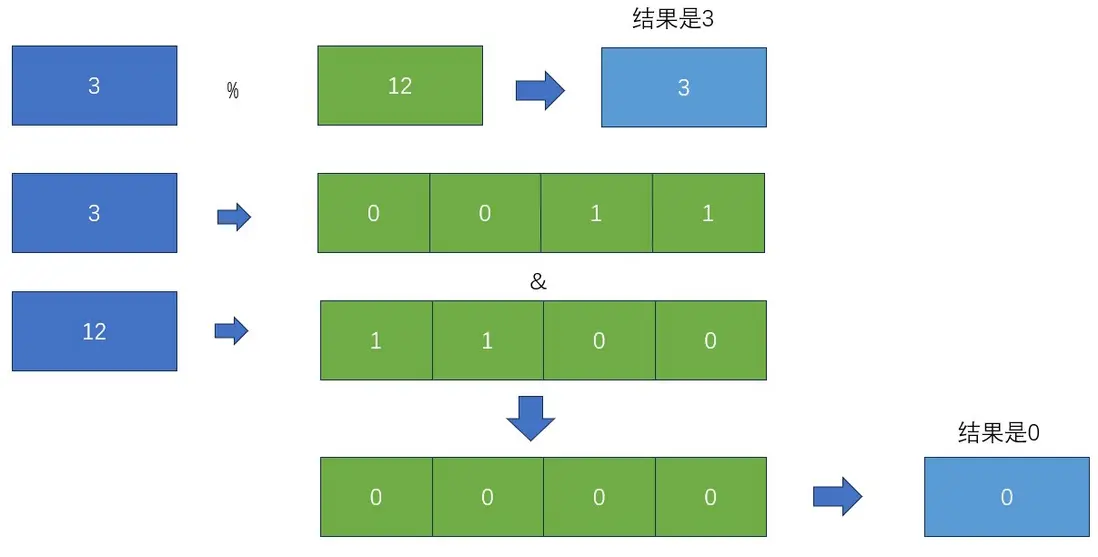
現在來區z = x & y 的取值區間,首先對於x和y,我們取的都是正整數,所以在進行與運算的時候,不會出現小於0的數,那能不能取到0呢,我們上面已經有一個例子了,也就是 3 & 12 , 我們得到了0,於是我們可以知道區間的左端點就是0,那右端點呢,相同置1,不同為0, 所以對於&運算來説,兩個數相等的時候得到相同值,所以最大值也是y。但這隻得到了取值區間,並沒有拿到我們想要的結果,但並不能得出c恆等於z。
想了一下,這裏推導下去不好推導,於是我們考慮用數學歸納法去證明,於任意正整數x和y=2n+1(n=1,2,3,4...),z=x&y恆等於c=x%y,首先我們取n = 1,則y = 3,也就是説x & 3 = x % 3,如果x=3n,也就是3的倍數,則x%3=0,現在我們來看x & 3的值,我們求證x = 3n(n = 1 , 2 , 3...), x & 3 = 0, 還是用數學歸納法,但是當n = 1的時候,就是不對的,比如3 & 3 = 3 , 而 3 % 3 = 0,因此往下證明,也沒有什麼價值。
也許應該換一種思路,我們觀察一下對x是正整數,y是奇數,取x在[1,12],然後對x & y,取y = 13來觀察結果結果為: [1,0,1,4,5,4,5,8,9,8,9,12,13,12,13], 感覺這個算法在13這個奇數表現的不如取餘算法,於是想到了HashMap的默認大小是16,那麼下標範圍應當是0到15,取餘結果為:1到15。這到和取餘結果是一致的。只是對數字取餘不好,我們還是討論初始大小是15,單純的做&運算,導致衝突的概率是比較高的,我們舉個例子來説明這個情況,15的二進制表示是00000000 0000000000001111。
我們隨意取幾組hash值 : 101001011100010000100101、10100111 11000100 00100101、11100111 11000100 00100101,會發現計算出來的數組位置都跑到了5位置上:
我們應當發揮高位的價值,讓高位也參與運算,於是HashMap的選擇是讓高16位與低16位進行&運算進行碰撞:
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}也就是高半區和低半區或異或,就是為了混合原始哈希碼的高位和低位,以此來加大低位的隨機性。而且混合後的低位摻雜了高位的部分特徵,這樣高位的信息也被變相保留下來。我們不妨給這種操作取一個好聽的名字就叫擾動函數吧。那看來HashMap要做防禦性處理了,不能隨便的制定容量,我們不能隨便制定容量,HashMap會總是尋找給定容量最近的2的次冪。
記着來看put 方法
如果hash相同,但是調用equals方法不同,説明出現了hash衝突,然後看對應位置的節點是否是樹節點,也就是我們上面提到的紅黑樹,如果樹將其添加到樹裏面。否則準備開始遍歷鏈表,將其添加到最後,然後判斷鏈表的長度是否大於8,如果大於8,然後轉換紅黑樹,插入鍵值對。這是我之前知道的,但是我在看源碼有點不理解:
static final int TREEIFY_THRESHOLD = 8;
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}TREEIFY_THRESHOLD - 1 = 7,不應該是等於8嘛,但是我們是從0開始的,所以0到7剛好等於8,沒毛病。如果判斷出來鏈表的某個節點和放入的key 是一個,也就是:
e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))然後我們接着看語句塊七:
// 語句塊七
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}putVal中onlyIfAbsent是false,所以覆蓋value。在HashMap中afterNodeAccess是空方法,交給LinkedHashMap來實現。這個onlyIfAbsent為true, 應該是給putIfAbsent用的。
public V putIfAbsent(K key, V value) {
return putVal(hash(key), key, value, true, true);
}也就是如果key不存在才放進去,如果存在了就返回給結果:
Map<String,String> map = new HashMap<>();
map.put("email","xxx");
System.out.println(map.putIfAbsent("email", "aaa"));
// 相當於putIfAbsent
if (map.get("email") == null){
map.put("email","aaa");
}想起來JDK 1.8 ConcurrentHashMap中putIfAbsent的性能問題:
final V putVal(K key, V value, boolean onlyIfAbsent) {
if (key == null || value == null) throw new NullPointerException();
int hash = spread(key.hashCode());
int binCount = 0;
for (Node<K,V>[] tab = table;;) {
Node<K,V> f; int n, i, fh;
if (tab == null || (n = tab.length) == 0)
tab = initTable(); // 初始化表
else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) { // 如果為空通過CAS賦值
if (casTabAt(tab, i, null,
new Node<K,V>(hash, key, value, null)))
break; // no lock when adding to empty bin
}
else if ((fh = f.hash) == MOVED)
tab = helpTransfer(tab, f);
else {
V oldVal = null;
// 性能問題就在這,都已經存在了還是加鎖。
synchronized (f) {
// 省略無關代碼
if (tabAt(tab, i) == f) {}
}
}
addCount(1L, binCount);
return null;
}在JDK 17這個問題得到了修復:
final V putVal(K key, V value, boolean onlyIfAbsent) {
if (key == null || value == null) throw new NullPointerException();
int hash = spread(key.hashCode());
int binCount = 0;
for (Node<K,V>[] tab = table;;) {
Node<K,V> f; int n, i, fh; K fk; V fv;
if (tab == null || (n = tab.length) == 0)
tab = initTable();
else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) {
if (casTabAt(tab, i, null, new Node<K,V>(hash, key, value)))
break; // no lock when adding to empty bin
}
else if ((fh = f.hash) == MOVED)
tab = helpTransfer(tab, f);
// 既然已經存在了不需要加鎖
else if (onlyIfAbsent // check first node without acquiring lock
&& fh == hash
&& ((fk = f.key) == key || (fk != null && key.equals(fk)))
&& (fv = f.val) != null)
return fv;
else {
V oldVal = null;
synchronized (f) {
if (tabAt(tab, i) == f) {}
}
}
addCount(1L, binCount);
return null;
}回到語句八、九、十:
// 語句塊八
++modCount;
// 語句塊九
if (++size > threshold)
resize();
// 語句塊十
afterNodeInsertion(evict);threshold: size超過這個觸發擴容,也就是容量乘以負載因子,默認負載因子是0.75,這個容量我們可以通過HashMap的構造函數傳入:
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
this.loadFactor = loadFactor;
this.threshold = tableSizeFor(initialCapacity);
}static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}modCount用於跟蹤修改次數,這個的用處是用於禁在用迭代器遍歷的時候一邊添加一邊移除,添加的時候增加modCount,用迭代器遍歷的時候remove會進行判斷:
abstract class HashIterator {
Node<K,V> next; // next entry to return
Node<K,V> current; // current entry
int expectedModCount; // for fast-fail
int index; // current slot
HashIterator() {
expectedModCount = modCount;
Node<K,V>[] t = table;
current = next = null;
index = 0;
if (t != null && size > 0) { // advance to first entry
do {} while (index < t.length && (next = t[index++]) == null);
}
}
public final void remove() {
Node<K,V> p = current;
if (p == null)
throw new IllegalStateException();
// 比較現有的modCount和剛初始化迭代器的expectedModCount
if (modCount != expectedModCount)
throw new ConcurrentModificationException();
current = null;
K key = p.key;
removeNode(hash(key), key, null, false, false);
expectedModCount = modCount;
}
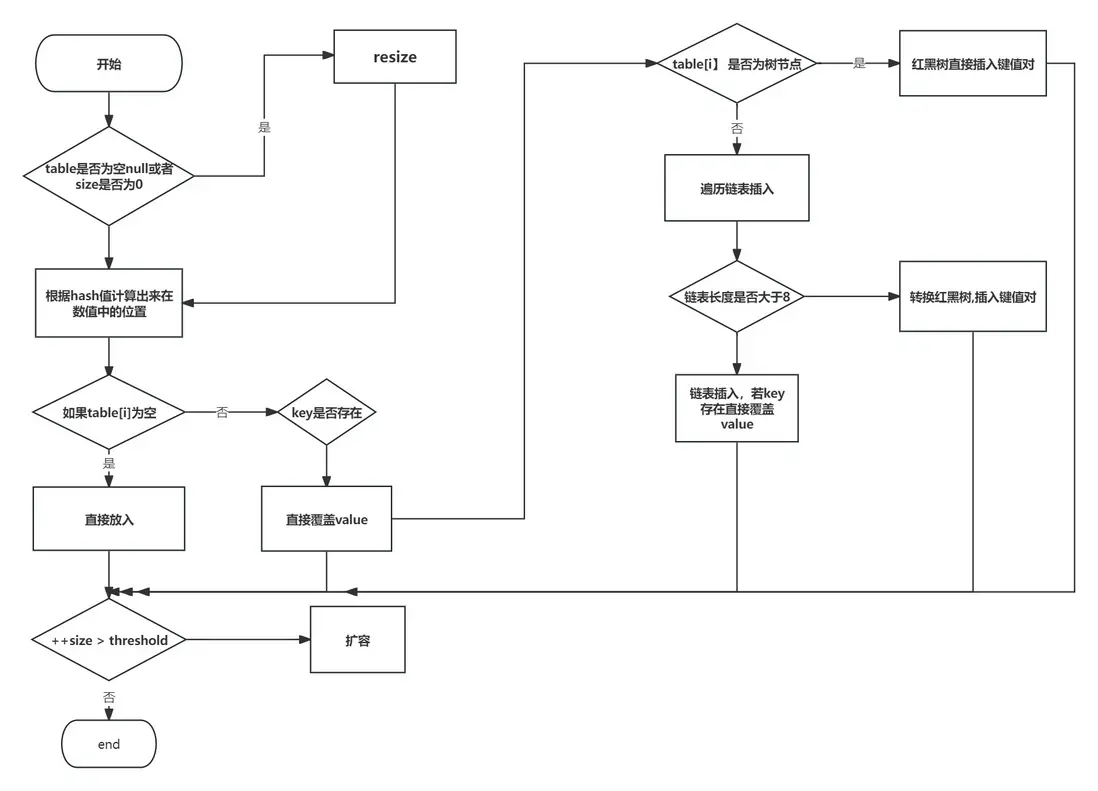
}所以總結一下put方法的邏輯如下:
① 首先判斷table是否為空,如果為空執行初始化操作
② 如果為空放入,++size,如果不為空,計算hash值計算出來在數組的位置,然後判斷對應位置是否有值
③ 如果相等hash方法和equals相等,則執行覆蓋。如果不相等就判斷是否是樹節點,如果是紅黑樹直接插入鍵值對。
④如果是鏈表,遍歷鏈表插入,然後判斷鏈表的長度是否大於8,大於8,執行樹化。
⑤ 如果小於8,通過hash方法和equals方法判斷是否有相同的結點,有執行覆蓋。
總結一下
本篇我們經過探索得到了什麼呢,我們對HashMap的思路有了一個更加清晰的認知,我們常用的String類採取的hash算法屬於hash算法中的多項式算法,為什麼是31傳統如此,當然可能是為了方便給編譯器做優化,優化為(i << 5 ) -i,這樣相對快一些。
原則上調大31的值會,降低哈希衝突,但是int類型的值前後合計起來有40億個,這太大了,我們不可能聲明這麼大的數組,於是我們需要通過運算將哈希值映射到對應的數組位置上,剛開始數組比較小,如果直接取餘,高位的哈希值不會發揮作用,因此HashMap引入了擾動函數,增加碰撞概率,降低哈希衝突,為了使用位運算替代取餘運算符,HashMap將數組的初始容量大小防禦性的設置為2的次冪,即使你指定容量,HashMap也會自動尋找指定值更靠近的2的次冪數。
我們同時也看了HashMap的put流程,對put流程進行了梳理。
參考資料
[1] Java 8系列之重新認識HashMap https://tech.meituan.com/2016/06/24/java-hashmap.html
[2] Why does Java's hashCode() in String use 31 as a multiplier? https://stackoverflow.com/questions/299304/why-does-javas-hashcode-in-string-use-31-as-a-multiplier
[3] JDK 源碼中 HashMap 的 hash 方法原理是什麼? https://www.zhihu.com/question/20733617
[4] HashMap.tableSizeFor(...). How does this code round up to the next power of 2? https://stackoverflow.com/questions/51118300/hashmap-tablesizefor-how-does-this-code-round-up-to-the-next-power-of-2