💡 學而不思則罔,思而不學則殆。 —— 孔子
👉 微信公眾號已開啓,菜農曰,沒關注的同學們記得關注哦!
本篇帶來的是蔣文華老師編寫的《博弈論:每個人都能成為決策高手》
什麼是博弈?字面描述中,博弈由兩個字構成:博 和 弈。博弈是一種雙方(多方)的對抗(比賽),對抗總是在一定的規則下進行,參與者必然會考慮應用相應的策略(計謀),並儘可能讓自己獲勝。
博弈論設計甚廣,後續發展基本上沿着以下4個方面展開:
- 對 納什均衡 的弱化(或一般化)研究
- 對 納什均衡 的精煉(或篩選)研究
- 對 博弈論 的基本假設的深入研究
- 對 博弈論 的應用研究
事實上,博弈論早已從單純對經濟問題的研究發展成為對社會問題的研究,並且在經濟學以外的政治學、社會學、管理學等眾多領域都得到了廣泛應用。
基於博弈論的重要性,小菜針對 《博弈論》 一書進行了筆記摘要,相信博弈論將成為解釋衝突、建立合作、增進信任、促進社會經濟發展的重要理論。
文中講述了多種博弈模型,貼近生活也耐人尋味。
一、概覽
1)博弈類型和結構化思維
科學的起點是分類,只有通過分類才能區分事物之間的不同。
衣服會進行分類,書籍會進行分類,甚至身高、收入、智商等都能夠進行分類。有了分類,事物才會變得有序。
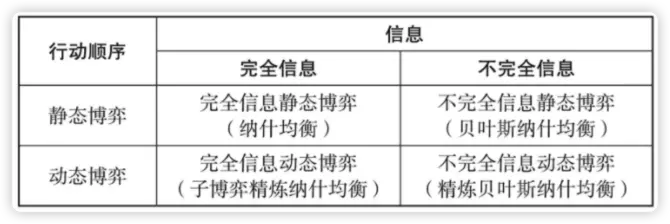
博弈的分類有兩種
- 靜態博弈 和 動態博弈
- 完全信息博弈 和 不完全信息博弈
靜態博弈和動態博弈
- 靜態博弈是指在博弈中,參與者同時選擇或雖非同時選擇單後行動者並不知道先行動者採取了什麼具體行動(雖然在物理時間上不是同時的,但是在邏輯時間上是同時的)
- 動態博弈是指在博弈中,參與者的行動有先後順序,且後行動者能夠觀察到先行動者所選擇的行動
以上推演到實際生活中:
石頭剪刀布、投標活動就是 靜態博弈
棋牌遊戲、拍賣就是 動態博弈
有個實實在在的例子:
每個學校在課程結束後,都會要求學生給老師的課程評分,老師也需要對學生的成績評分,如果學生先評分,那麼可能會影響到老師做出成績評分,如果老師先評分,那麼可能也會影響到學生做出課程評分。那麼這樣一來,老師和學生之間就會相互牽制,難以確保評分真實有效。因此就會採取保密的方式,學生先評分,但是對老師保密,老師在進行學生成績評分後的一段時間才能看到學生對自己的評分。而這就是一種 靜態博弈
兩者區別:
靜態博弈 的參與者只能依據對對手策略或行動的想象做決策,比如 "石頭剪刀布" 的遊戲,你只能想象着對方會出"石頭",然後你決定出"步"。
動態博弈 的參與者則是依據對手的實際選擇做決策。
完全信息博弈與不完全信息博弈
- 完全信息博弈 是指在博弈過程中,每個參與者對其他參與者的類型、策略空間以及損益函數的信息都有準確的瞭解。
- 不完全信息博弈 就是與完全信息博弈相反,總有一些信息不是所有參與者都知道的。
以上推演到實際生活中:
教育、醫療和金融就是 不完全信息博弈
相比之下,完全信息博弈 少之又少,真實反映:生活本來就是不公平的
結構化思維
當某樣東西可以從兩個及以上不同的維度進行分類的時候,如果把兩個維度組合在一個平面上,就可以構建出一種結構化的組合方式。
將上面説到4種博弈類型進行組合,我們可以得到:
2)擴展認知
納什均衡
均衡是指所有博弈參與者的最優策略組合。
納什均衡的釋義就是:給定你的策略,我的策略就是對我而言最好的策略(或之一);給定我的策略,你的策略也是對你的來説最好的策略(或之一),雙方在對方給定的策略下已經沒有積極性調整自己已選的策略。
簡言之:雙方到了冷熱化的底部,沒有人願意偏離自己給定的策略狀態
策略探究
策略的三大屬性:
- 策略的完整性
策略必須是完整的,意味着參與者把所有可能的情況都加以充分考慮,沒有任何遺落(需善於利用分類,窮盡法)
- 策略的多樣性
策略總是多樣的,意味着你其實有很多個策略可以選擇(A、B計劃,留有一手,有備無患)
- 策略的不可觀察性
策略不同於行動,行動是具體的做法,策略是對行動的預想。根據一個人的行為來推測一個人的策略有可能是錯的(你以為的總是你以為的)
應急預案四要素
- 完整又清晰的信息分類,不能有遺漏
- 責任到人的明確規定,遇到情況不能沒有負責人
- 提前準備好詳細又可行的行動方案,讓大家提前知道怎麼應對
- 時效性,讓大家知道每一種行動的具體時間要求
一般來説,策略依託四個相關的認知要素:多種多樣的知識與經驗,豐富和全面的想象力,出奇甚至超強的聯繫構建能力,在現實條件下梳理與過濾策略可操作性的能力。
理性假設
理性是一個非常寬泛而又很難界定的概念
理想的三個標準:
- 偏好的完備性和情境理性
人對A、B的偏好一定是基於某一特定的情境而言的。好比一個例子:出售一本雜誌,雜誌具備了電子版和印刷版,那麼如何定價比較合理?
方案A:
- 電子版 59 美元
- 印刷版+電子版套餐 125 美元
基於這種套餐,實驗結果有 68% 的人數選擇電子版,而組合版只有 32%
方案B:
- 電子版 59 美元
- 印刷版 125 美元
- 印刷版+電子版套餐 125 美元
這種方案的定價難免有些讓人摸不到頭腦,還會有人買印刷版嗎?答案是否定的,但是你的目的是為了銷售組合版,情況會比 方案A 好轉嗎,實驗證明,有 84% 的人選擇了組合版,而 16% 選擇了電子版。
以上案例充分説明,人對事物的偏好既取決於自身,也取決於具體的情境(所謂套餐就是把你套住的餐)
所有的判斷和選擇都基於某個參照系,不同的參照系會導致不同的判斷和不同的選擇
- 偏好的可傳遞性
偏好的可傳遞性是指一個人如果認為 A 比 B 好,B 比 C 好,那麼一定認為 A 比 C 好。偏好的可傳遞性可以確保一個人能在一堆東西中區分出好壞,選出自己最喜歡的東西。
如果偏好不具備可傳遞性,那麼面對兩個以上的選項時,選擇就會變得隨機和混亂,你的行為選擇是無法被預測的,但可受到人工干擾。
好比一個例子:
如果你對水果的偏好是這樣的:蘋果和桃子比,更喜歡蘋果;桃子和荔枝比,更喜歡桃子;荔枝和蘋果比,卻更喜歡荔枝。對方只要控制水果的擺放順序,就能控制你的選擇結果。先給你看蘋果和桃子,再給你看荔枝,你就選了荔枝;先給你看蘋果和荔枝,再給你看桃子,你就選了桃子;先給你看桃子和荔枝,再給你看蘋果,你就選了蘋果。
- 偏好的中庸性
偏好的中庸性是指如果一個人認為 A 和 B 一樣好,那麼介於A,B中間的C就是一個更讓人喜歡的選擇。偏好的中庸性告訴我們,雖然每個人的偏好不同,但如果兩端是一樣的,那中間就是更好的。
共同知識
什麼是共同知識呢?
皇帝的新裝 是一個家喻户曉的故事,但是皇帝沒穿衣服,這是每個人都知道的 共有知識,但不是 共同知識,共同知識是每個人不但都知道(共有),而且也知道其他人都知道,而且都知道其他人知道每個人都知道...
我們平常所説的 共識 其實就是 共同知識 ,兩者概念我們要加以區分。(不由想到互聯網中著名的 兩將軍問題,TCP 為什麼要進行 三次握手,而不是兩次握手?就是為了達成共識)
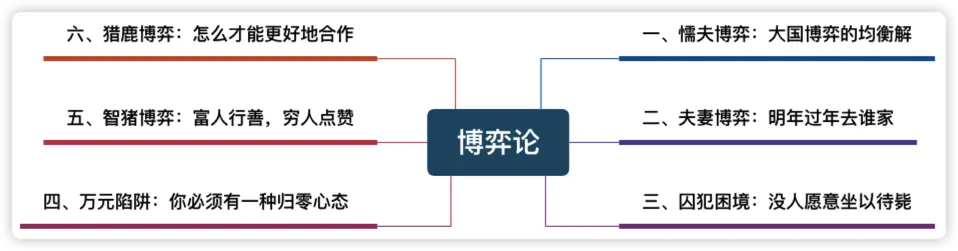
二、經典模型
1)懦夫博弈
狹路相逢勇者勝 就是一種博弈,雙方都在堵對方先退一步。
説起這種博弈,《速度與激情》中太多場景就是 懦夫博弈 的映照。
在懦夫博弈中,有兩個參與者A和B,每個參與者有兩種策略(行動):進和退。雙方面臨四種結果:都進、都退、A進B退、A退B進。
懦夫博弈存在先動優勢,一旦有一方選擇了進,另一方的選擇只能是退,否則會遭到更大的損失,所謂的 "先下手為強後下手遭殃"。
從理論上來説,懦夫博弈的制勝策略是:搶先選擇進,並搶先告訴對方已經選擇了進,同時讓對方知道自己的選擇已經無法更改了
一句話中,體現了三要素:
- 搶先選擇進
- 讓對方知道自己選擇了進
- 讓對方知道自己沒有退路
因此,懦夫博弈中的先動優勢既是基於 行動的先動優勢,又是基於信息傳遞的先動優勢
贏者通吃會導致過度競爭,在這種博弈中,需要反覆估量自己勝出的可能性,一般情況下選擇不參與博弈是理性的。
2)夫妻博弈
夫妻間的博弈可謂不斷,明年過年去誰家也成為了世紀難題。
這個問題的背景下,存在雙方的共同利益。在夫妻博弈中,我們可以找到兩個純策略的納什均衡:都去男方家過年或都去女方家過年。
從現實生活中分析,一般有三種情況:
- 與懦夫博弈一樣存在先動優勢,家庭地位決定納什均衡的偏好
- 輪流去對方家
- 隨機選擇,這種解決方案比納什均衡還有效,雙方基於共同認可的規則。
提前商定合作收益的分配機制 :在所有的合作關係中,都會涉及合作收益的分配問題。不同的分配模式都有其存在的合理性,關鍵是合作之前先自願約定,這樣可以極大地降低合作成本。
夫妻博弈是一種共贏的合作博弈,但在合作的收益分配上存在差異。提前約定合作收益的分配是避免矛盾衝突的有效手段。
3)囚犯困境
囚犯困境又稱“囚徒困境”,是博弈論中最為經典的理論模型之一。
囚犯困境在現在電視劇中屢見不鮮,大致場景為:兩個罪犯進行分開審訊,如果兩人都保持沉默,那麼只能以犯罪事實定罪,可能判處的罪行就比較輕。但如果有一個人可以先坦白,那麼這個人就可以當場釋放,另一個人承受加重罪罰,如果兩個人都坦白,不但不會被釋放,還會加重處罰。
這個時候 囚犯困境 就出現了,對於兩人來説最佳結果便是雙方都選擇抗拒,但對於個人來説便是先坦白,這才是佔優策略
佔優策略:採用該策略的結果都優於其他策略,由博弈中的所有參與者的佔優策略組合所構成的均衡便是佔優策略均衡
上述情境是在雙方不能溝通的情況下,條件放寬後,允許兩人帶上10分鐘,再決定是否坦白。
那麼此時博弈的方向就會變成雙方是否遵守約定,當然,最好的選擇依然是不遵守約定,最終的結果也取決於是否某一方能夠具備在心理上不會有單獨背叛對方的。
囚犯困境在現實中是無處不在的。對於囚犯困境的原因,人們一般理解為參與人對於自身利益的追求,因此有利益衝突的地方,往往就是一種囚犯困境。那麼如何走出囚犯困境?
- 努力修改遊戲規則。努力尋找每個人的佔優策略,做不到讓利於人,也要做到共利與人
- 尋求道德的力量。如果沒有某種道德準則來約束人類的行為,那麼人類社會與動物世界並無區別
- 藉助歷史的記憶。把對歷史的記憶轉為對未來的想象
囚犯困境的究極原因在於:每個人讓自己利益增加,是以他人利益的更大損失為代價
囚犯困境帶來的啓示:博弈的均衡結果和事實的真相無關,只取決於博弈的規則
4)萬元陷阱
這個博弈帶來了一個十分有意思的案例:
有個《美元拍賣遊戲》,在遊戲中,蘇必克把1美元紙幣作為拍品,當眾拍賣,拍賣的規則是:出價最高的人獲得拍品,出價第二高的人也要付出所出價格的款項。
什麼意思呢?現將10000元錢拍賣給大家,請大家互相競價,以100元為加價單位,直到沒有人再加價為止。出價最高者以其所出價格獲得10000元錢,同時,出價第二高者也得將其所出價格的金錢數量付給我。
如果在場的人都沒人蔘與競拍,那麼你只要以 100 元就可以獲取到 10000元,淨賺 9900 元。
當然以上是最佳的理想結果,如果有兩人在不斷加價,當你出到 1000 時,另一人出了 1100 ,你是否願意放棄,如果你此時放棄就會損失 1000 元,那唯一的方法便是繼續加價,冷熱化持續中,當你已經加到 9900 元時,對方已經出價到了 10000 元,這個時候雙方都不願放棄,因此雙方又在不斷加價,甚至直到破產。
這就是著名的 萬元陷阱 ,這些陷阱通常有三個特徵:
- 一個明顯的誘餌
- 通往誘餌之路是單向的,可進不可出
- 參與者越想掙脱就會陷得越深,變得不能自拔,最後為此付出慘痛的代價
那麼如何避免 萬元陷阱?
- 確立你投入的極限及預先的約定
- 極限一經確立,就要堅持到底,一定不要輕易改變
- 自己打定主意,儘量不受他人影響,避免出現 從眾心理
- 不斷提醒自己繼續投入的代價
有趣的競價方式:不要想着天上掉餡餅,直接開9900的價錢,只有100元的利潤,一般情況下也不會有人繼續加價,除非搗亂,但如果真的有人加價到 10000元,如果你決定繼續加價,那就拿出 破釜沉舟 的行動,直接從 9900 加價到 19900 元,讓對方意識到,如果再次加價到 20000 元,也是損失 10000 元,如果放棄也是損失 10000 元,而加價到 20000 元可能還會面臨着你繼續加價,增加損失。
避免萬元陷阱最有效的策略就是及時止損,不要深陷其中,二是不要相信天上會掉餡餅,利小才不至於引起對方的強烈嫉妒和垂涎,如果血很多,會把狼招來的
5)智豬博弈
什麼是智豬博弈呢?經典模型如下:
假設豬圈裏有兩頭豬,一頭大,一頭小。豬圈的一側放有食槽,另外一側安裝着控制豬食供應的按鈕,按一下會有10個單位的豬食進槽,但是按動按鈕的成本是2個單位的豬食。
情況1:如果兩頭豬一起按按鈕,再一起跑過去吃,那麼大豬會吃到 7 個單位,小豬吃到 3 個單位。減去成本,大豬:5,小豬:1
情況2:如果大豬去按按鈕,小豬在食槽旁等着吃,那麼大豬會吃到 6 個單位,小豬吃到 4 個單位。減去成本,大豬:4,小豬:4
情況3:如果小豬去按按鈕,大豬在食槽旁等着吃,那麼大豬會吃到 9 個單位,小豬吃到 1 個單位。減去成本,大豬:9,小豬:-1
3種情況很明顯,對於小豬來説 等 是佔優策略,那麼在小豬一定等的情況下,想要吃到豬食,大豬隻能按,那麼這種情況的納什均衡便是 (大豬按,小豬等)
但是這種均衡對大豬來説並不是佔優策略,畢竟多勞並不能多得,最終的收益是(大豬:4,小豬:4)。在這個博弈模型中,對於小豬而言,無論如何都不會按按鈕,大豬去不去按隻影響小豬的損益,不會影響小豬的策略或行為選擇。
因此這種模型也可以稱為 搭便車博弈,一方付出了相應的代價,雙方共享了所得到的收益。通過這種模型我們可以得到以下啓示:
- 個體理性與集體理性是相互衝突,還是相一致,取決於制度安排本身
- 收入分配的不均將有助於個體理性與集體理性的衝突。也就是讓一部分人先富起來有助於幫助未富的人。
- 富人願意行善,離不開窮人的點贊。想讓大豬去按按鈕,小豬可以選擇少吃一點,讓大豬覺得不會過於不平衡
- 能力越大,責任越大
在猜謎博弈中有兩個非常重要的概念:純策略 和 混合策略
純策略: 參與者在每一個給定信息情況下只選擇一種特定的行動
混合策略:參與者在給定信息情況下,以某種概率分佈隨機地選擇不同的行動
比如“人不犯我,我不犯人;人若犯我,我必犯人”是一個純策略。“人不犯我,我80%的可能性不犯人;人若犯我,我90%的可能性會犯人”就是一個混合策略
6)獵鹿博弈
又是一個有趣的博弈模型
兩個人出去打獵,獵物為鹿和兔。
情況1:如果兩個人獨自去打兔子,一天下來可以打到2只兔子
情況2:如果要打鹿,則需要兩個人一起去,缺一不可。(一隻鹿的價值相當於8只兔子,每個人相當於4只兔子)當然如果只有一個人去打鹿,另一個沒去,那麼去打鹿的那個人收益為 0
分析發現,該模型下存在兩種納什均衡,便是要麼一起去打鹿,要麼一起去打兔子。
但是去打鹿就需要承擔有一方未去打鹿的風險。那麼這種情況下就需要 提前溝通
如果溝通成本小於最終獲利成本,那麼就要提前溝通,相互合作使利益最大化。溝通和協調成本越低,人與人之間就越容易建立合作關係
人生無處不博弈。博弈論雖然誕生的很晚,但它的作用卻無處不在,學點博弈論的知識,可以讓我們持有一種前向的視角去看待問題,即對於即將發生的事情進行一番理性的推演,從而找到最大的可能性,然後讓自己做出相對好的決策。
不要空談,不要貪懶,和小菜一起做個 吹着牛X做架構 的程序猿吧~點個關注做個伴,讓小菜不再孤單。咱們下文見!
👀 今天的你多努力一點,明天的你就能少説一句求人的話!
👉🏻 微信公眾號:菜農曰,沒關注的同學們記得關注哦!