簡介

中序遍歷（LDR）是二叉樹遍歷的一種，也叫做中根遍歷、中序周遊。

定義

在二叉樹中，中序遍歷首先遍歷左子樹，然後訪問根結點，最後遍歷右子樹。若二叉樹為空則結束返回，否則：（1）中序遍歷左子樹（2）訪問根結點（3）中序遍歷右子樹

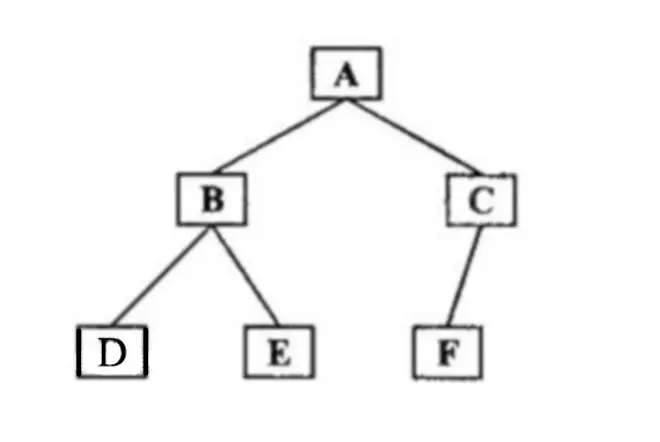
如圖所示二叉樹，中序遍歷結果：DBEAFC

Golang遍歷實現

// TreeNode Definition for a binary tree node.
type TreeNode struct {
    Val   int       // 根
    Left  *TreeNode //左節點
    Right *TreeNode //右節點
}

func inorderTraversal(root *TreeNode) (res []int) {
    var inorder func(node *TreeNode)
    inorder = func(node *TreeNode) {
        if node == nil {
            return // 結束當前遞歸
        }
        inorder(node.Left)          // 直接懟到左邊最下邊
        res = append(res, node.Val) // 添加到數組裏
        inorder(node.Right)         // 看右邊還有沒有分支，有就繼續走，沒有就將右節點加入數組
    }
    inorder(root)
    return
}

Golang迭代實現

棧：先進後出

// TreeNode Definition for a binary tree node.
type TreeNode struct {
    Val   int       // 根
    Left  *TreeNode //左節點
    Right *TreeNode //右節點
}

func inorderTraversal(root *TreeNode) (res []int) {
    stack := []*TreeNode{}    // 定義一個棧，棧存的就是一棵樹
    for root != nil || len(stack) > 0 {
        for root != nil {
            stack = append(stack, root)  // 1.先將整顆樹懟進去，在把所有的左子樹懟進去
            root = root.Left   // 2.遍歷左子樹，直接左邊的最下邊
        }
        root = stack[len(stack)-1]  // 3.因為先進後出，拿到了最下面的左節點
        stack = stack[:len(stack)-1]
        res = append(res, root.Val) // 4.懟到數組裏
                //5.看以右節點為根的還有沒有左節點，有就回到上面第1步，沒有就走第3步，把根節點
        root = root.Right // 
    }
    return
}