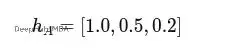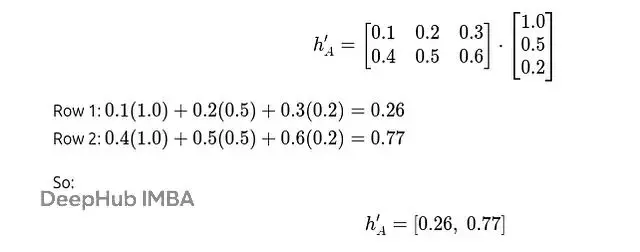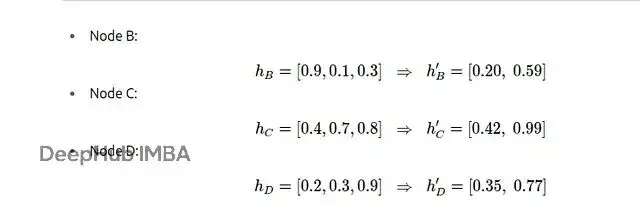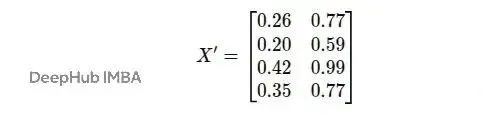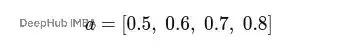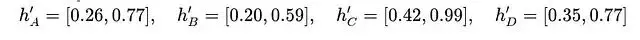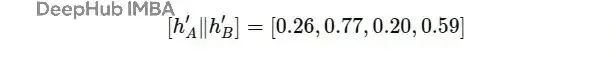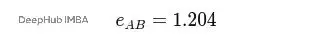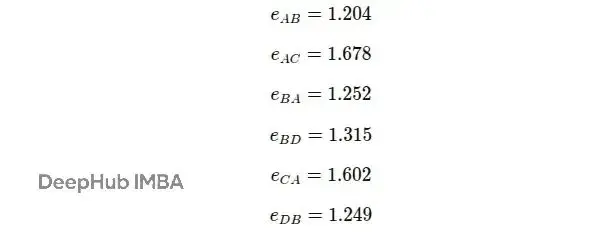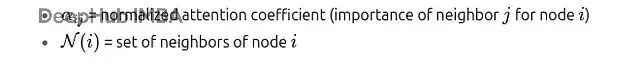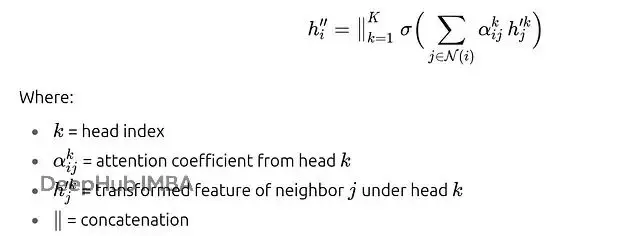圖數據在機器學習中的地位越來越重要。社交網絡的用户關係、論文引用網絡、分子結構，這些都不是傳統的表格或序列數據能很好處理的。現實世界中實體之間的連接往往承載着關鍵信息。

圖神經網絡(GNN)的出現解決了這個問題，它讓每個節點可以從鄰居那裏獲取信息來更新自己的表示。圖卷積網絡(GCN)是其中的經典代表，但GCN有個明顯的限制：所有鄰居節點的貢獻都是相等的（在歸一化之後）。

這個假設在很多情況下並不合理。比如在社交網絡中，不同朋友對你的影響程度肯定不一樣；在分子中，也不是所有原子對化學性質的貢獻都相同。

圖注意力網絡(GAT)就是為了解決這個問題而設計的。它引入注意力機制，讓模型自己學會給不同鄰居分配不同的權重，而不是簡單地平均處理。用一個比喻來説，GCN像是"聽取所有朋友的建議然後求平均"，而GAT更像是"重點聽那些真正懂行的朋友的話"。

本文文會詳細拆解GAT的工作機制，用一個具體的4節點圖例來演示整個計算過程。如果你讀過原論文覺得數學公式比較抽象，這裏的數值例子應該能讓你看清楚GAT到底是怎麼運作的。

GAT的核心思想

GAT的設計目標很直接：讓每個節點能夠智能地選擇從哪些鄰居那裏獲取信息，以及獲取多少信息。

任何圖都包含三個基本要素：節點(V)代表圖中的實體，邊(E)表示實體間的關係，特徵(X)是每個節點的屬性向量。

GAT層的工作流程可以概括為：輸入節點特徵，通過線性變換投影到新的特徵空間，計算節點間的注意力分數，用softmax進行歸一化，最後按注意力權重聚合鄰居信息得到新的節點表示。

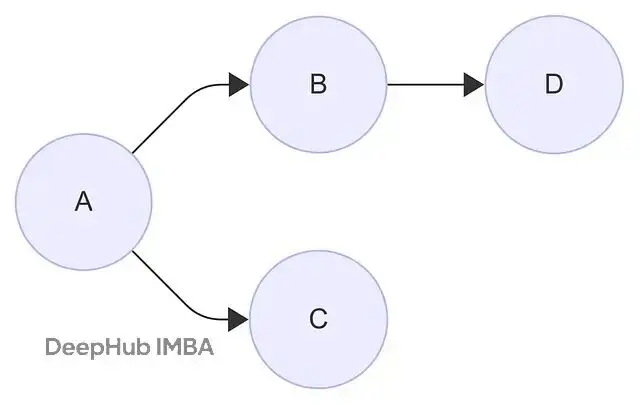
我們用一個簡單的4節點圖來演示這個過程。節點A、B、C、D的連接關係如下圖所示：

為了便於手工計算，我們設定每個節點的特徵維度為3：

• 節點A：[1.0, 0.5, 0.2]
• 節點B：[0.9, 0.1, 0.3]
• 節點C：[0.4, 0.7, 0.8]
• 節點D：[0.2, 0.3, 0.9]

把這些特徵向量按行排列，就得到了特徵矩陣 X ∈ ℝ⁴ˣ³：

矩陣的每一行對應一個節點，每一列對應一個特徵維度。我們有4個節點，每個節點3個特徵，所以是4×3的矩陣。

線性變換：特徵投影

GAT計算注意力之前，需要先對節點特徵進行線性變換。這一步用共享的權重矩陣W將原始特徵投影到新的特徵空間。

線性變換的作用有兩個：一是讓模型能學到更好的特徵表示，二是可以調整特徵維度來適應不同任務的需要。數學表達式是：

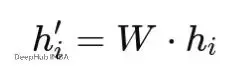
我們設定原始特徵維度F=3，變換後的維度F′=2，權重矩陣W的值為（實際應用中這些權重是隨機初始化然後訓練得到的）：

以節點A為例，它的原始特徵向量是：

與權重矩陣W相乘得到：

對所有節點進行同樣的變換：

變換後的特徵矩陣是：

現在每個節點都從3維特徵變成了2維特徵。

注意力分數計算

有了變換後的特徵，接下來要計算注意力分數。這些分數反映了在信息聚合時，一個節點對另一個節點的重要程度。

對於邊(i,j)，注意力分數的計算公式是：

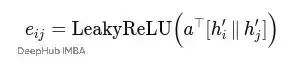
這裏eij可以理解為鄰居j對節點i的"原始重要性分數"。

設定變換後的特徵維度F′=2，注意力向量a為（實際中這個向量也是訓練學習得到的）：

使用前面得到的變換特徵：

計算邊A→B的注意力分數。首先將節點A和B的特徵連接起來：

然後與注意力向量a做點積：
0.5(0.26) + 0.6(0.77) + 0.7(0.20) + 0.8(0.59) = 1.204

應用LeakyReLU激活函數（由於結果是正數，值保持不變）：

用同樣的方法計算其他邊的注意力分數：

到這裏得到的是未歸一化的注意力分數，它們可以是任意實數。下一步需要用softmax對這些分數進行歸一化，讓它們變成類似概率的形式，便於比較和使用。

Softmax歸一化：注意力權重分配

現在有了每條邊的未歸一化注意力分數eij，但這些原始分數的數值範圍不一致，沒法直接比較。一個節點的分數可能在1.0左右，另一個節點的分數可能在5.0左右。

Softmax函數能夠解決這個問題，它將每個節點的所有鄰居注意力分數轉換為概率分佈：

其中：

Softmax確保每個節點對其所有鄰居的注意力係數加起來等於1。

以節點A為例進行計算：

結果顯示節點A給B分配38.3%的注意力，給C分配61.6%的注意力。

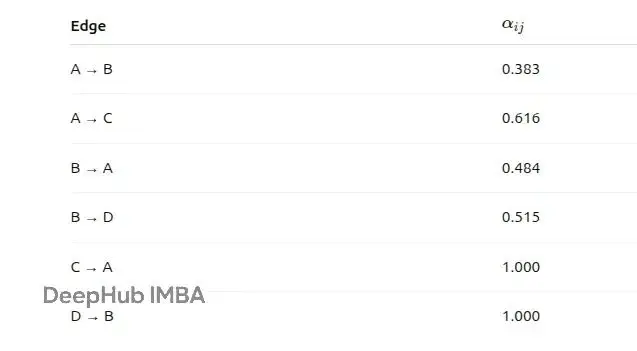
所有節點的歸一化注意力係數如下表：

從這些結果可以看出：節點A更偏向於關注節點C而不是B；節點B在A和D之間的注意力分配比較均勻；節點C和D各自只有一個鄰居，所以所有注意力都分配給了那個鄰居。

特徵聚合：生成新的節點表示

有了注意力係數αij，每個節點就可以通過聚合鄰居的特徵來更新自己的表示了：

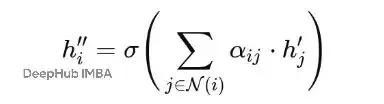
簡單説就是：用重要性權重對每個鄰居的特徵進行加權，求和後再應用激活函數。

節點A的聚合計算過程：

所有節點聚合後的特徵：

• 節點A：[0.335, 0.836]
• 節點B：[0.306, 0.769]
• 節點C：[0.260, 0.770]
• 節點D：[0.200, 0.590]

激活函數σ通常使用ELU（Exponential Linear Unit）。對於正數ELU直接保持原值；對於負數ELU會進行平滑處理而不是像ReLU那樣直接置零，這種設計讓模型能夠學習到比線性組合更復雜的模式。

注意力機制決定了鄰居的重要性，聚合過程則產生了融合鄰居信息的新節點表示。

多頭注意力：多視角信息融合

前面介紹的是單個注意力頭的工作方式：變換特徵→計算注意力→softmax歸一化→聚合鄰居信息。

實際應用中，GAT會同時使用多個注意力頭，這個設計借鑑了Transformer架構。

多頭機制的好處很明顯。單個注意力頭可能會過度偏向某個鄰居（比如節點A對C的偏好過強），多個頭可以提供不同的視角來平衡這種偏向。每個頭都有自己的權重矩陣Wk和注意力向量ak，它們關注鄰域的不同方面。在中間層不同頭的輸出通常會被拼接起來；在最終層則通常取平均值來產生最終預測。

對於K個注意力頭，節點i的更新表示為：

假設我們用2個頭處理4節點圖。頭1可能學會讓節點A給C分配70%權重，給B分配30%權重；頭2可能學會相反的分配策略，給C分配40%權重，給B分配60%權重。當我們把兩個頭的結果拼接起來時，節點A的最終嵌入就包含了兩種不同的鄰居關係視角。

這種多樣性讓模型的表達能力更強，避免陷入單一的注意力模式。

GAT的訓練過程

GAT layer本身只是前向計算的一部分，訓練的目標是調整權重矩陣W^k 和注意力向量a^k，讓網絡在具體任務（比如節點分類）上表現更好。這些參數一開始是隨機初始化的，然後通過反向傳播不斷優化。

訓練流程比較標準：輸入包括圖G=(V,E)、節點特徵矩陣X ∈ ℝ^{N×F}，以及部分節點的標籤。前向傳播讓特徵通過各個GAT層，每層都進行特徵變換、注意力計算和鄰居聚合，最終層用softmax輸出每個節點的類別概率。

損失計算通常用交叉熵，但只針對有標籤的節點。反向傳播計算損失對參數的梯度，這些梯度會流經注意力機制，更新鄰居權重的分配策略。

優化器一般選Adam，學習率設在0.001到0.01之間。為了防止過擬合，會在節點特徵和注意力係數上應用dropout，同時對權重W加上L2正則化。

多頭訓練讓每個注意力頭學習各自的參數，專注於鄰域的不同特性。根據任務需要，頭的輸出要麼拼接（捕獲多個視角），要麼取平均（穩定預測）。

總結

GAT的整個工作流程可以用一句話概括：線性變換→注意力計算→softmax歸一化→特徵聚合=上下文感知的節點嵌入。

這套機制自動解決了很多實際問題。在社交網絡中誰對你影響更大，最好的朋友還是普通熟人？在分子結構中哪些原子主導了化合物的性質？在論文引用網絡中經典研究和普通引用的權重應該如何分配？GAT通過學習關係的相對重要性來回答這些問題。

當然GAT也有侷限性。在超大規模圖上，注意力計算的開銷比較高；在小數據集上，模型容易過擬合。但它已經成為圖學習領域最受歡迎的工具之一，廣泛應用於社交媒體分析、推薦系統、藥物發現等領域。

如果你理解了GAT的數學原理和計算過程，就可以考慮在自己的領域裏嘗試這個方法。不管是社交網絡、知識圖譜還是分子生物學，GAT都有很大的應用潛力。

https://avoid.overfit.cn/post/b1c7efd4b1004512a98ebf3fcecce8e7

作者：Adarsha Pandey