Scaling Laws 已經成為深度學習領域的共識：更大的模型配合更多數據效果往往更好。但當參數量攀升至百億乃至千億級別時一個棘手的問題是：訓練不穩定性。

現代大語言模型動輒堆疊數十甚至上百層，殘差連接、跳躍連接、跨層路由機制層出不窮。這些架構設計背後的邏輯就是為了改善梯度流、加快收斂、提升參數利用率。但是在實踐中這些技在大規模訓練時卻經常出現問題：損失函數突然飆升、梯度爆炸、表徵坍塌、訓練動態變得極度脆弱等等。

大語言模型的運作似乎依賴某種內部貝葉斯幾何結構，而許多依賴密集捷徑的現代架構，恰恰在無意中破壞了這種結構。

近期研究揭示了一個有趣的現象：Transformer內部確實在執行貝葉斯推理：只不過不是符號化的方式而是幾何化的。殘差流承載信念狀態的累積，注意力機制負責路由概率證據，內部表徵則沿着以不確定性為參數的低維流形演化。一旦架構改動擾亂了這種幾何結構，模型的可訓練性和可靠性都會受到影響。

流形約束超連接（Manifold-Constrained Hyper-Connections，簡稱mHC）正是在這個背景下提出的。它並非單純的優化技巧，而是一種架構層面的保護機制，確保模型在擴展過程中維持概率推理所需的內部幾何。

接下來的我們將三條近期研究脈絡串聯起來，講述一個關於架構、幾何與規模化的故事。

Transformer如何用幾何實現貝葉斯推理

殘差流承載信念狀態

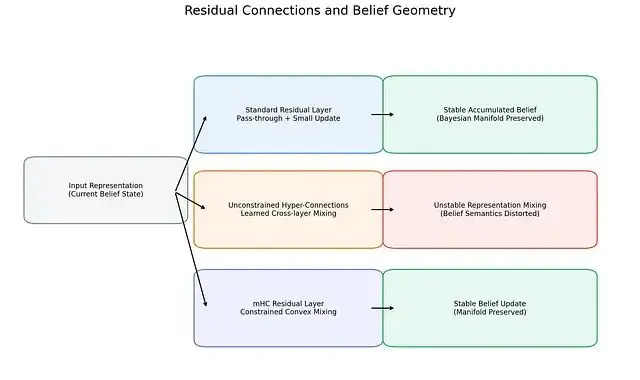
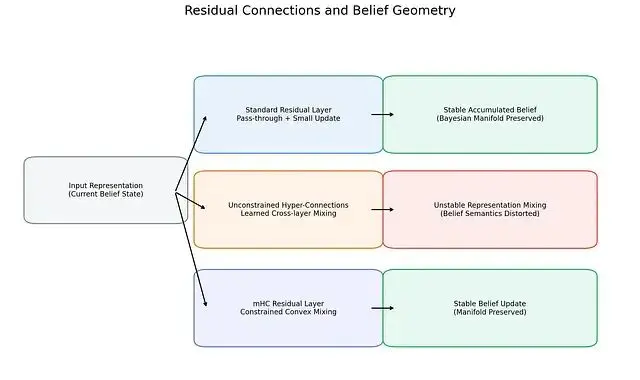
不同殘差連接模式對應着截然不同的內部信念動態。標準殘差連接通過增量式更新維持信念狀態的穩定；無約束超連接則引入任意的跨層混合，可能導致信念語義失真；mHC通過強制凸約束恢復穩定性，保護貝葉斯流形不受破壞。

大語言模型到底在"推理"還是僅僅在"模仿"？這個問題在自然語言任務上很難回答因為記憶和推理難以區分。

Aggarwal、Dalal和Misra另闢蹊徑，構建了所謂的"貝葉斯風洞"，這是一系列合成任務，真實貝葉斯後驗可以精確計算而單純記憶在理論上不可能奏效[1]。實驗結果是：小型Transformer能以接近機器精度的水平復現解析後驗而同等容量的MLP差距達幾個數量級。

從機制角度來看Transformer將推理過程拆解到不同組件：殘差流充當持久的信念狀態載體；注意力機制執行基於內容的尋址路由，篩選出信念的相關片段；前饋網絡（FFN）則負責數值化的後驗更新。

每一層都在精煉而不是覆蓋，這種組合式累積與貝葉斯濾波的邏輯類似：先驗 → 似然 → 後驗 → 新先驗。殘差連接的恆等保持特性在此至關重要：如果沒有的話信念狀態就無法在深度方向上穩定演進。

值向量匯聚於低維貝葉斯流形

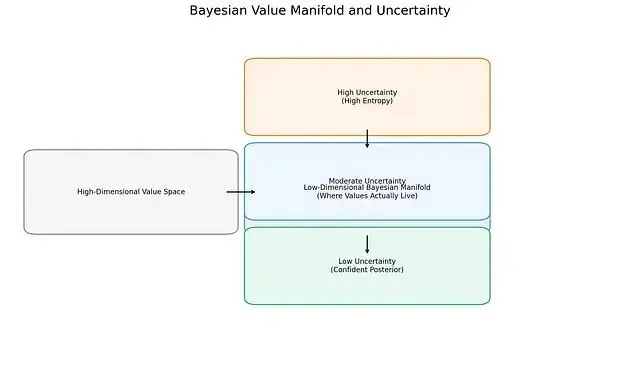
圖 2. 雖然Transformer的值向量定義在高維空間，但訓練使它們集中到低維貝葉斯流形上。沿流形移動對應不確定性的遞減：隨着各層整合更多證據，表徵從高熵狀態平滑過渡到低熵後驗信念。

在行為層面之外，模型內部則呈現出了幾何特徵[1]。鍵向量沿近似正交的假設軸排列；查詢向量隨着證據累積，逐步與這些軸對齊；值向量則分佈在一個以後驗熵為參數的低維流形上。

當不確定性降低時表徵沿流形平滑移動，這時後驗熵本身成了幾何座標。

訓練過程中還存在一個有意思的時序分離：注意力模式會較早固化下來形成固定的"推理框架"，而值表徵持續精煉以提升後驗"精度"。也就是説Transformer先學會"該關注什麼"之後才逐漸學會"如何精確編碼"。

梯度下降暗含EM算法

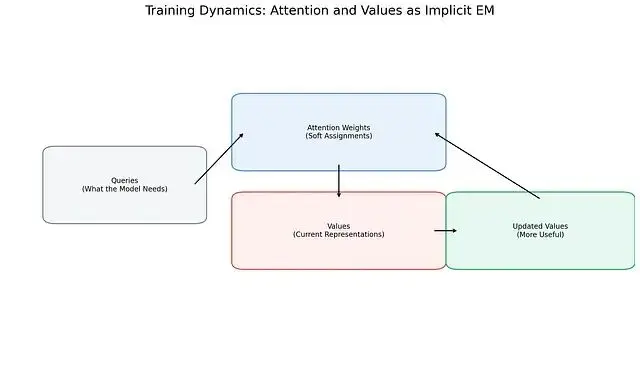
圖 3. 訓練過程中注意力與值表徵形成正反饋迴路。注意力權重為值分配軟性重要性，值則通過梯度下降更新以更好服務於關注它們的查詢。這種動態酷似隱式EM過程：注意力扮演軟分配角色，值充當自適應原型。

這種幾何結構為何會“涌現”？

對注意力梯度動態的分析給出瞭解釋[2]。在交叉熵損失下注意力分數與值向量之間存在正反饋循環：注意力會向那些減誤差能力高於平均水平的值傾斜，值則朝着最關注它們的查詢方向更新。

這與EM算法的結構高度相似：注意力權重相當於E步的軟責任分配，值向量更新相當於M步的責任加權原型調整，查詢和鍵則定義了假設框架。

關鍵在於這是雙時間尺度過程：路由先穩定，內容後精煉。整個動態成立的前提是信號傳播穩定、梯度有界。激活值一旦爆炸或消失，類EM機制隨即瓦解。

所以可以説貝葉斯流形並非偶然產物，它是梯度下降在幾何穩定環境中運行的雕刻結果。

密集跨層捷徑的風險

恆等映射的隱性價值

標準殘差連接非常簡單：如果某層學不到有用的東西那麼信號就原封不動通過，這確保了深度對應於增量式精煉。

超連接（Hyper-Connections, HC）對殘差進行了泛化，拓寬殘差流並在層與流之間引入可學習的混合矩陣[3]。表達能力確實增強了，但固定的恆等路徑也因此消失。殘差混合一旦完全可學習恆等保持便不再有任何保障。

規模放大的累積效應

無約束混合矩陣深度堆疊時，與恆等矩陣的微小偏差會乘法式累積。實踐中的表現是：信號極端放大或衰減、梯度爆炸、大型HC模型訓練時損失突增[3]。

這些現象不只是優化層面的麻煩，它們預示着表徵語義的崩塌。

貝葉斯幾何的破壞

貝葉斯推理依賴信念的序貫精煉，無約束跨層混合把來自不同推理階段的信念狀態混在一起彷彿它們本就兼容。

在幾何上表徵跳離了後驗流形；注意力-值的專門化變得飄忽不定；校準精度下降；隱式EM機制失效。密集的跳過鏈接打破了貝葉斯推理賴以運作的組合結構。

流形約束超連接（mHC）的設計思路

將殘差幾何投影到雙隨機矩陣空間

mHC的核心思想是把殘差混合矩陣投影到Birkhoff多面體——即雙隨機矩陣的空間[3]。這類矩陣非負，行和列加總均為1，恆等矩陣恰好位於其中心。

關鍵屬性的恢復

投影約束帶來了幾項重要保證。範數得以保持，信號不會爆炸也不會消失；輸出始終落在先前信念狀態的凸包內，實現凸混合；層層堆疊仍能保持類恆等行為，保證組合閉包性。

mHC在保留寬殘差流靈活性的同時，重新引入了標準殘差連接原本提供的架構保障。

規模化的幾何視角

從貝葉斯幾何角度審視，mHC的價值不僅在於穩定訓練，它保護的是信念更新的內部語義。

模型規模擴大時，微小的幾何畸變會不斷累積。破壞恆等保持的架構，在指標暴露問題之前，就已經在悄悄侵蝕概率推理能力。

mHC的根本的觀察是：

規模化不只是參數量和數據量的堆砌，更是對那些讓學習穩定、推理有意義的幾何不變量的守護。

如果Transformer確實依靠幾何來推理，那麼保護這種幾何或許是擴展未來模型時最關鍵也最容易被忽視的挑戰。

參考文獻

[1] N. Aggarwal, S. R. Dalal, V. Misra. The Bayesian Geometry of Transformer Attention. arXiv:2512.22471 (2025).

[2] N. Aggarwal, S. R. Dalal, V. Misra. Gradient Dynamics of Attention: How Cross-Entropy Sculpts Bayesian Manifolds. arXiv:2512.22473 (2025).

[3] Z. Xie et al. mHC: Manifold-Constrained Hyper-Connections. arXiv:2512.24880 (2025).

https://avoid.overfit.cn/post/b50b24b81a2146aeb9d711db38971d68

作者：Victor Sletten