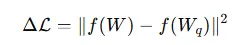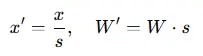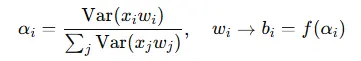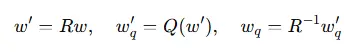一、引言

隨着大型語言模型（LLM）在具身智能等領域的廣泛應用，接下來就該思考如何在有限硬件資源下部署這些模型，量化是其中必不可少的步驟。

模型量化（Model Quantization）作為一種有效的模型壓縮技術，通過將模型中的浮點數參數轉換為低比特寬度的整數表示，顯著減少了模型的存儲和計算需求，同時儘量保持模型的性能。量化的基礎知識相信大家都不會陌生，例如必然要介紹兩種量化方式：PTQ/QAT。

QAT 是一種深度融合量化需求與模型訓練流程的技術，核心是在模型訓練階段主動嵌入 “偽量化算子”—— 不實際將參數轉換為低比特，而是模擬量化過程中的數值截斷誤差與舍入誤差，讓模型在學習任務知識的同時，同步適應量化帶來的精度損耗。訓練中，偽量化算子會實時統計各層輸入輸出的數據分佈（如激活值的極值、權重的方差），動態優化量化參數（如縮放因子、零點），確保量化邏輯與模型參數更新形成配合。這種 “邊訓練邊適配量化” 的特性，能讓大語言模型（LLM）在低精度表示（如 4bit、2bit）下，依然保留接近原始浮點模型的性能。

PTQ 是在 LLM 完全訓練完成後執行的量化方案，無需修改模型訓練流程，僅需使用少量校準數據（通常 100-1000 條代表性樣本）統計模型權重與激活值的分佈特徵，即可確定量化參數並完成低比特轉換。其核心優勢在於 “輕量高效”：無需重新訓練模型，量化過程僅需數分鐘至數小時，無需大規模計算資源；同時無需改動 LLM 架構，可直接適配各類推理框架，兼顧易用性與部署效率。不過，PTQ 的精度天花板相對較低，目前在 4bit 及以下量化時易出現明顯精度損失，更適合對精度要求不高、追求快速部署的場景。

本文重點不是上述兩種量化方式，而是將重點介紹四種主流的大模型量化方法：GPTQ、SmoothQuant、AWQ 和旋轉量化，下面來分別看一下。

二、GPTQ

GPTQ（Gradient-based Post-training Quantization）是一種後訓練量化方法，其核心思想是利用梯度信息來指導量化過程，從而最小化量化帶來的性能損失。論文中僅進行權重量化，權重被量化為 int4 類型，激活值為 float16。

GPTQ（GPT Quantization）是一種基於最優量化誤差最小化的單輪權重量化方法，其核心創新點在於：

• 順序壓縮算法：按重要性對模型層進行排序，優先量化對輸出影響較小的層
• 誤差補償機制：通過梯度下降優化量化參數，減少精度損失
• 分組量化策略：將權重矩陣分為小組（Group Size）獨立量化，平衡壓縮率與精度

工作流程圖如下：

GPTQ 通過優化量化誤差的目標函數，使得量化後的模型輸出儘可能接近原始模型的輸出。其優化目標可以表示為：

其中，f（⋅） 為模型的前向傳播函數，W 為原始浮點權重，Wq 為量化後的權重。

GPTQ 已被廣泛應用於 HuggingFace 等平台，具有完善的工具鏈和生態支持。但 GPTQ 主要針對模型的權重進行量化，對激活值的處理相對有限，且在量化過程中需要計算梯度信息，會增加額外的計算開銷。

三、SmoothQuant

SmoothQuant 是一種訓練後量化方法，旨在解決激活值量化困難的問題。核心理念在於平衡激活值和權重的量化難度。在大模型量化中，激活值通常包含大量離羣點，這些離羣點會顯著拉伸量化範圍，增加量化誤差。SmoothQuant 提出了一種基於平滑因子的逐通道縮放變換方法，對每個通道的激活值進行縮放以平滑其分佈，同時對權重施加反向縮放，確保模型計算的等價性。

其中，s 為平滑因子，x 為激活值，W 為權重，x′ 和 W′ 分別為經過平滑處理後的激活值和權重。通過這種方式，SmoothQuant 將激活值的量化難度轉移到權重上，從而實現更高效的量化。

SmoothQuant 可以同時對權重和激活值進行 8 位量化，減少模型的存儲需求，通過將激活值的異常值減少，SmoothQuant 可以提高推理的效率，但平滑因子 s 的選擇對量化效果有較大影響，且不同的模型可能需要不同的平滑因子，需要通過實驗進行調優。

四、AWQ

AWQ（Activation-aware Weight Quantization）是一種自適應權重量化方法，旨在根據激活值的重要性來指導權重的量化過程。其核心思想是識別出對模型輸出影響較大的激活值，並根據這些激活值的重要性來調整權重的量化精度。具體而言，AWQ 通過計算激活值的方差來評估其重要性，然後根據重要性為權重分配不同的量化精度：

其中，

$$ \alpha_i $$

為第 i 個權重的激活感知度，$$b\_i$$ 為其對應的量化比特數。

AWQ 方法源於"權重對於 LLM 的性能並不同等重要"的觀察，存在約（0.1%-1%）顯著權重對大模型性能影響太大，通過跳過這 1% 的重要權重不進行量化，可以大大減少量化誤差。根據激活值的重要性動態調整權重的量化精度，這需要計算激活值的方差，實現相對複雜。

五、SpinQuant

旋轉量化（SpinQuant）是一種通過旋轉矩陣變換數據空間來實現量化的方法。其核心思想是通過引入旋轉矩陣 RRR 將數據映射到新的空間，然後在新的空間中進行量化，從而使得量化誤差在數據空間中更加均勻地分佈，減少量化誤差對模型性能的影響。具體而言，旋轉量化的過程可以表示為：

其中，w 為原始權重，w′ 為經過旋轉變換後的權重，$$w'\_q$$ 為量化後的權重，$$w\_q$$ 為最終的量化權重。

通過旋轉變換數據空間，可以使得量化誤差在數據空間中更加均勻地分佈，適應不同的模型結構和數據分佈，減少量化誤差。這個過程需要計算旋轉矩陣，並進行矩陣變換，會引入一些計算開銷。