地圖投影

為了更好地展示地球上的數據，需要將地球投影到一個平面上。地圖投影是一個數學問題，按照一定的幾何關係，將地球上的經緯度座標映射到一個平面上的座標。地球投影有很多種，每種投影都有自己的優缺點。本文介紹一些常用的地球投影。

什麼是地圖投影

投影，在數學上的含義是建立兩個面之間點與點、線與線的對應關係。同樣地，地圖投影的定義是：建立地球橢球面(或球體表面)與地圖平面之間點與點或線與線的一一對應關係。

地圖投影的變形通常有長度變形、面積變形和角度變形。在實際應用中，根據地圖的使用目的，通常會限定某種變形。

地球是一個球體，而我們的屏幕是一個平面，所以我們需要將地球投影到一個平面上，這樣才能在屏幕上顯示地球的數據。

目的

• 方便看圖或者展示地理信息；
• 製作平面地圖；
• 建立投影座標系；
• 氣象學分析；

種類

把球形的地球投影到平面上，一定會有形變或者扭曲，這種形變有很多種，不同的投影方式會有不同的形變。根據變形性質，常見的地圖投影有：

• 等角投影(正形投影)：保持線和線的夾角不變，這是關注的的重點；
• 等面積投影：保持面積不變；
• 等距投影：保持距離不變；
• 等形狀投影：保持形狀不變；

等角投影保證了角度不變，也就保證了方向不變，使用該投影可以保證地圖上的方向是正確的，這種地圖投影適合用於航海、飛行等需要方向準確的領域。是我們關注的重點。

等角投影的分類

• 極地投影
• 蘭伯特投影
• 墨卡託投影

重點介紹墨卡託投影，因為它是日常開發中遇到最多的投影方式。

墨卡託投影

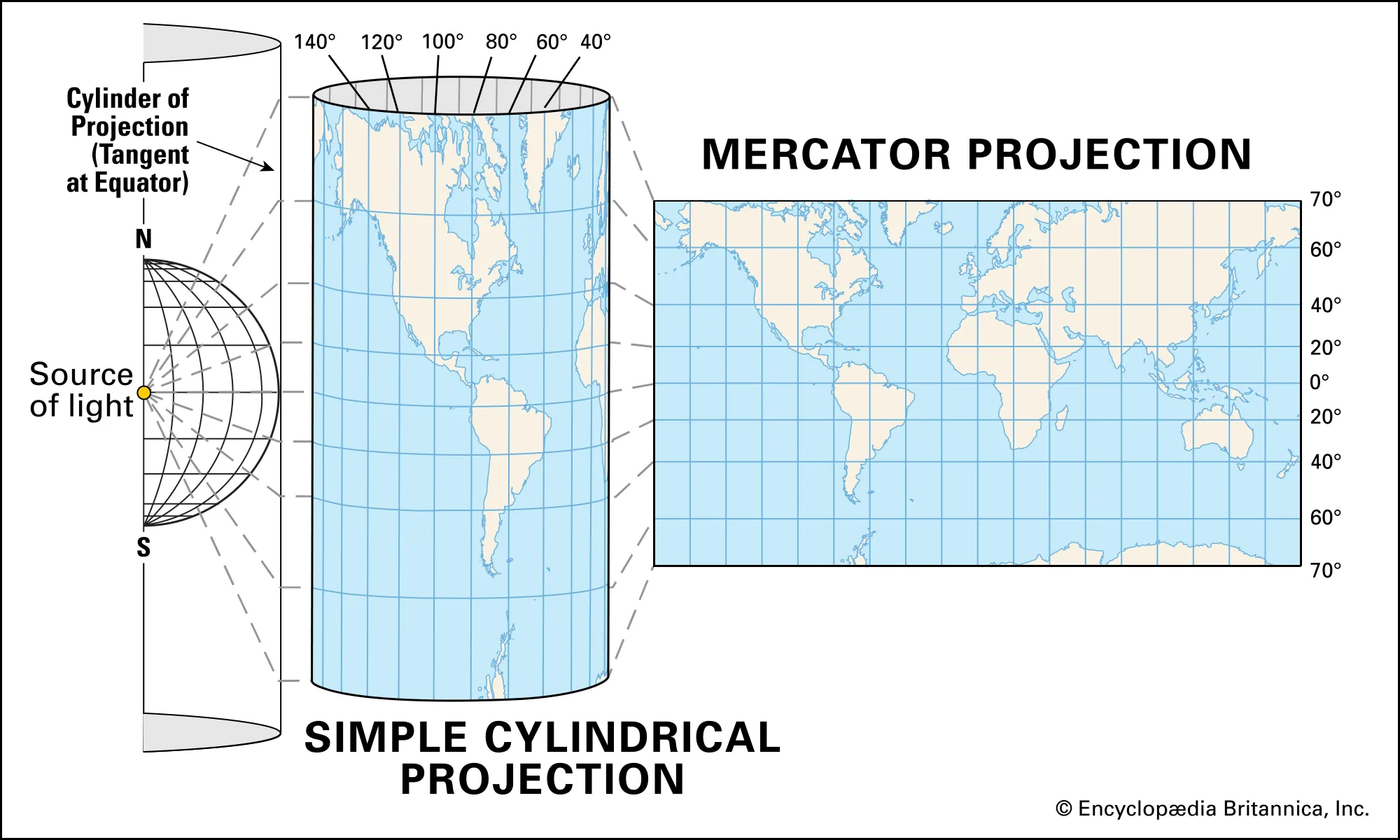
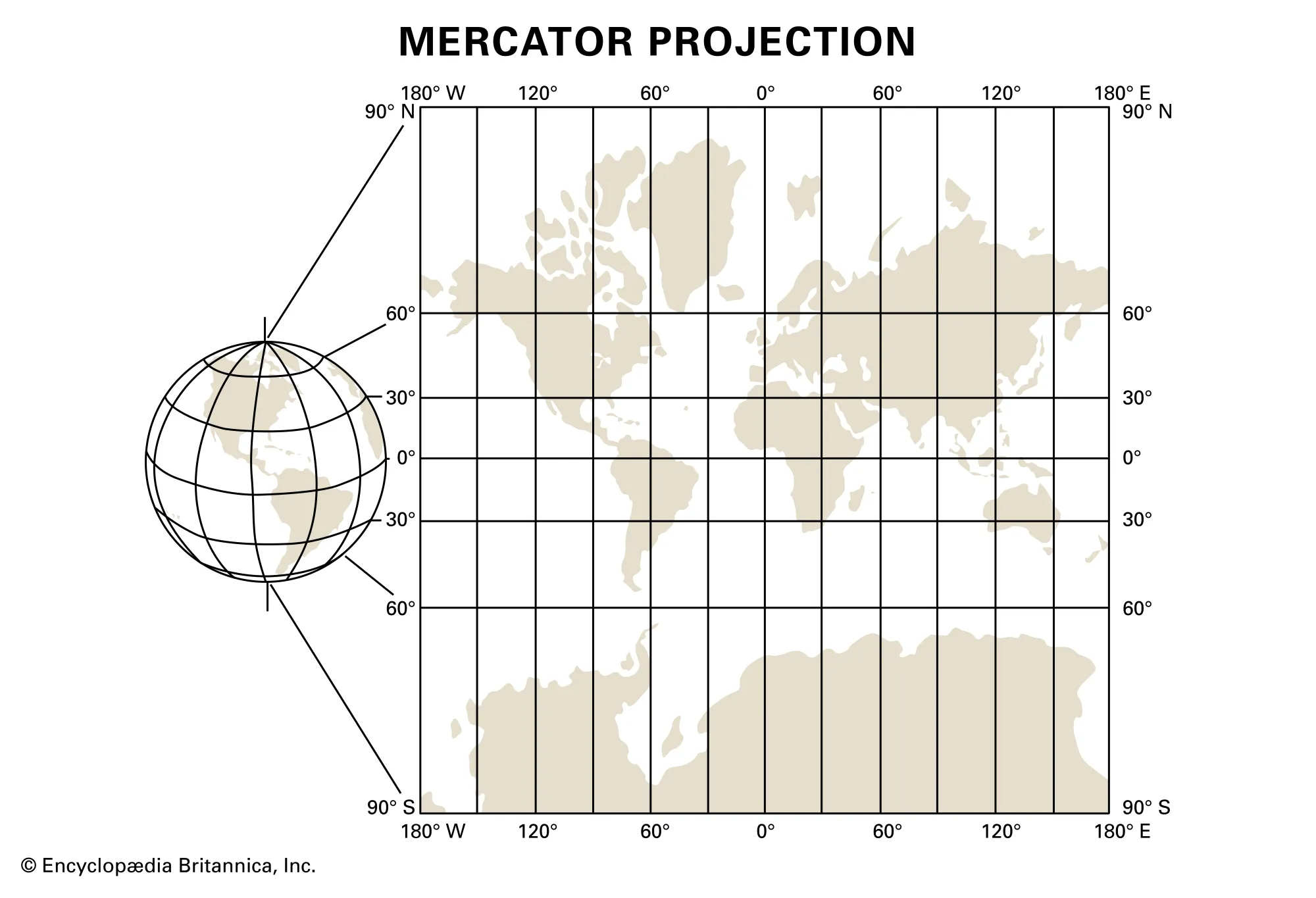
1569年，由比利時數學家墨卡託（Gerardus Mercator）提出的一種地圖投影方法，是最常用的地圖投影方法之一。墨卡託投影是一種等角圓柱投影，它將地球表面投影到一個圓柱體上，然後再展開到一個平面上。

一個圓柱體套住地球，光線從球心射出。

墨卡託投影的特點是保持角度不變，是一種等角投影，地球上兩直線的夾角，投影到平面上，角度不變，但是會有面積變形，即在地圖的高緯度地區，面積會被放大。由於等角不變的特點，保證了投影后方向和相對位置不變，因此墨卡託投影在航海、飛行等需要方向準確的領域中應用廣泛。

Web 墨卡託投影

2005年，Google Maps 推出，使用 Web 墨卡託投影，這種投影方式在 web 地圖中得到了廣泛應用，已經是 web 地圖的事實標準。

EPSG 投影編碼為 3857，即 EPSG:3857 。

地球是一個兩極扁赤道略長的橢球體，而 Web 墨卡託投影把地球簡化成一個正球體，兩極半徑和赤道半徑相等了。

web 墨卡託水平方向(經度方向)沒有變形，但是豎直方向(維度方向)隨着維度的變大，長度被拉伸了，維度越高，拉伸越大。

經過 web 墨卡託投影以後，以赤道為標準緯線，本初子午線為中央經線，兩者的交點為原點，向東、向北為正，向西、向南為負。

赤道半徑R = 6378137米, PI = 3.14159265359, 則

X 軸範圍：[-20037508.342789244, 20037508.342789244], 而 Y 軸，從投影上看，越靠近極點，會被拉伸到無窮遠，google 的工程師乾脆就取和 X 一樣的範圍，因此世界地圖是一個正方形。

最小座標為[-20037508.342789244, -20037508.342789244]，最大座標 [-20037508.342789244, 20037508.342789244]。

合法的經緯度範圍為： [-180, -85.06, 180, 85.06] 。

為何是 85.05 呢？

我計算出來是 71.57 。

計算方法是：

tanX = PI*R/R = PI = 3.14159265359
X = 71.57

後在網上查詢資料，發現是 85.06 ，原因是：

y = ln(tan(π/4 + φ/2)) # 當 φ = 85.06 時，tan(π/4 + φ/2) = ∞

不太明白這個公式，但是可以理解，因為墨卡託投影在極點處會無限拉伸，所以不能顯示。

參考

陳志強同學-b站課程 - 投影

墨卡託投影是怎麼把一個“球”變成一張“圖紙”的呢？

Web Mercator 公開的小秘密

投影、座標與瓦片

小結

• 地圖投影是將地球投影到一個平面上，以便展示地球上的數據；
• 地圖投影有很多種，每種投影都有自己的優缺點；
• 墨卡託投影是一種等角投影，保持角度不變，適合航海、飛行等需要方向準確的領域；
• Web 墨卡託投影是一種等角投影，保持角度不變，但是會有面積變形，緯度越高變形越嚴重，適合 web 地圖展示。