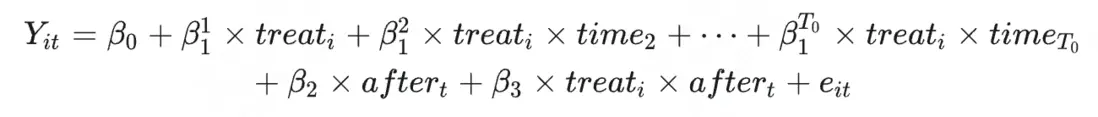本文系《可信實驗白皮書》系列的第五篇文章，上一篇我們圍繞隨機輪轉實驗展開，內容主要包括拋硬幣隨機輪轉、完全隨機輪轉、配對隨機輪轉等幾個實驗方法的介紹。本篇我們會介紹準實驗，然後會重點介紹雙重差分法，包括概述、評估原理及美團的一些實踐案例。

準實驗（Quasi-experiment）適用於“實驗設計者”可干預分組，但無法隨機分配實驗單元至實驗組和對照組的場景。經典隨機對照實驗通過隨機分配實驗單元，保證了實驗組和對照組的可觀測特徵和不可觀測特徵分佈都是相同的，差異僅在於樣本是否受策略影響，因此兩組觀測結果的差異可以歸因於策略影響。然而，在一些無法隨機分配樣本的場景下，實驗組和對照組的特徵分佈往往不一致，進而導致兩個組在未施加策略時就存在差異，此時需在滿足部分特定條件假設的前提下使用準實驗評估方法，才能夠比較準確地估計策略的效果。

以美團履約業務場景為例，以下幾個因素可能阻礙進行時空粒度的隨機實驗。

溢出效應+小樣本等多重約束下無法開展時空隨機實驗：

• 溢出效應：履約業務是一個典型的多邊場景，容易造成實驗單元間相互依賴和影響，而簡單的隨機對照實驗，通常會違背個體處理穩定性假設（SUTVA），進而造成實驗偏差。在這種存在溢出效應的履約業務場景中，實驗有時需要在地理上隔離樣本，以避免或者減少溢出效應，一種典型的做法是依據地理位置將一個城市劃分為兩個半城，將實驗組和對照組之間的運力溢出等限制在半城交界處，將溢出效應的影響儘量降至最低。
• 小樣本：履約策略大多以配送區域為基本單元，即使是區域溢入溢出效應模型也通常要求配送區域數量至少超過20個。但是部分城市規模較小，可供分析建模的配送區域數量達不到該要求，因此也無法採用隨機分組+溢出效應建模的實驗方案。

策略和產品的特殊性：部分策略和產品的特殊性限制了隨機分組。例如，配送區域優化策略考慮在保障整體覆蓋範圍不變且區域之間不重疊的約束下，對區域進行邊界優化甚至合併，然而對於2個相鄰的區域，在該約束下，優化A區域邊界必然會導致B邊界跟隨變化，因此從產品形態上無法實現A區域邊界變更但B區域邊界維持不變，此時不能考慮按區域隨機分流。

綜上所述，考慮到美團履約業務場景的特殊性，許多實驗無法採用隨機對照實驗準確量化策略效果，因此發展一套標準的準實驗設計與評估流程尤為必要。接下來，我們着重介紹經典的準實驗方法——雙重差分法，關於雙重差分法的衍生和其他準實驗方法，請參考文末的拓展部分。

5.1 雙重差分法

5.1.1 方法概述

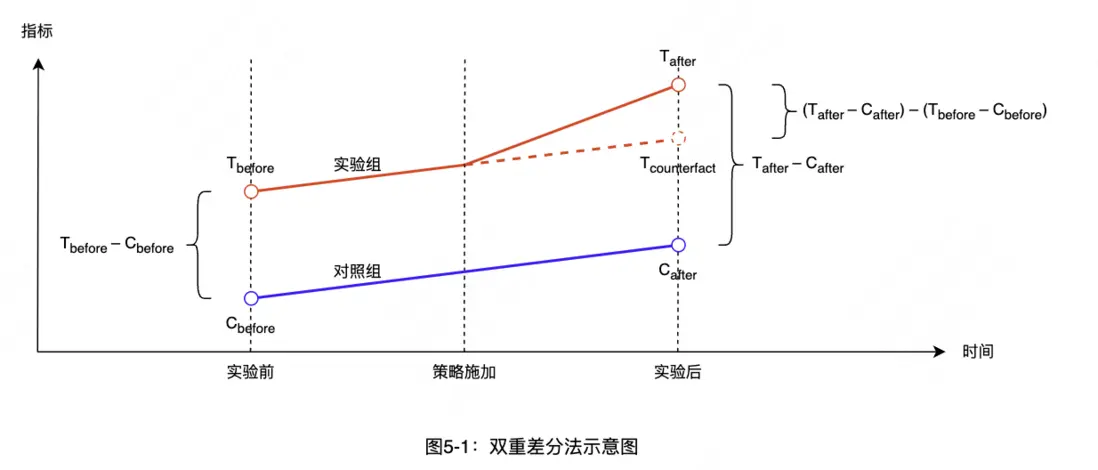
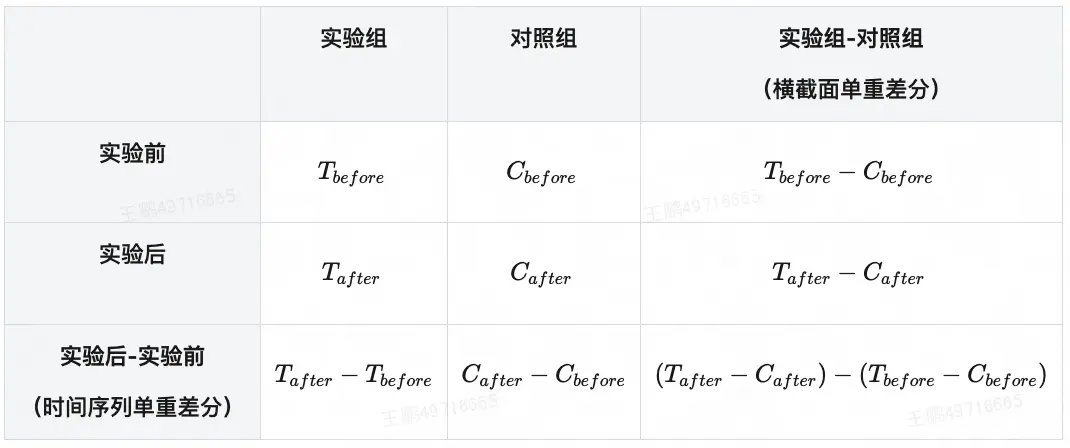
雙重差分法（Difference in differences，簡稱DID）的基本思想，就是用實驗後的實驗組、對照組差異減去實驗前的實驗組、對照組差異，來估計策略在實驗組上的效果（ATT），圖5-1直觀展示了該思想。下面先從單重差分開始，逐步解析雙重差分法。

消除了兩組之間的固有差異，這就是雙重差分法的基本原理。

5.1.2 評估原理

本節我們將詳細介紹雙重差分法的數學模型和原理，包括傳統DID模型、固定效應模型、平行趨勢假設合理性檢驗等。

傳統DID模型

基本雙重差分法模型的形式為：

固定效應模型

平行趨勢假設合理性檢驗

平行趨勢假設是使用雙重差分法估計策略效果的關鍵假設。平行趨勢假設要求，在沒有策略影響的情況下，實驗組和對照組的差異不隨時間變化是恆定的，即實驗組和對照組的趨勢保持平行。一種簡單的平行趨勢檢驗方法是通過畫圖觀察平行趨勢是否滿足，但是這種方法比較粗糙。為了得到更加嚴謹的量化結果，可以使用模型進行平行趨勢檢驗。在此基礎上一種方法是將DID模型拓展為以下形式：

5.1.3 平行趨勢分組

不難看出，平行趨勢假設是影響雙重差分實驗結論可信度的關鍵。因此，為了儘量保證實驗結論的可信度，我們建議採取下述平行趨勢分組，以儘量保障“實驗組”、“對照組”平行趨勢假設的合理性：

1. 隨機劃分2個半城為實驗組和對照組；
2. 使用實驗前數據，對所有目標指標和護欄指標做平行趨勢檢驗，根據通過檢驗的模型和實驗組對照組差異對本次分組進行打分（通過固定效應模型平行趨勢檢驗的分組得分更高，兩組差異更小的分組得分更高）；
3. 重複步驟1和步驟2若干次，選取得分最高的分組作為最終分組。

儘管採取平行趨勢分組的做法在實驗設計上儘量保障平行趨勢假設的合理性，但在實際場景中仍存在以下潛在風險，因此在實踐中優先考慮隨機實驗，隨機實驗不可行時才考慮雙重差分實驗：

1. 平行趨勢是一個比較強的假設，在樣本量較少時，有時難以劃分滿足平行趨勢的實驗組和對照組；
2. 平行趨勢檢驗只能檢驗實驗前的平行趨勢以證明假設的合理性，實驗後的平行趨勢是否滿足是無法得知的，並且無法得到完全保證，在某些情況下平行趨勢假設會受到挑戰：

a. 有不可控的外部因素影響時，平行趨勢假設可能被打破，此時可考慮適當剔除不可控因素影響日期再進行評估分析；

b. 評估指標的數值限定範圍，可能影響到平行趨勢。在履約場景中準時率指標時常被關注，準時率的數值範圍在0～100%之間並且通常處於較高水位，在某些極端情況下如果平行趨勢成立，實驗組準時率的反事實結果可能會超過其上限100%，這時平行趨勢假設與實際情況會略有出入。

5.1.4 實驗案例

實驗案例：配送區域優化實驗

實驗背景：為解決現有配送區域劃分畸形、切割商户熱力等問題，提升配送效率，通過算法智能規劃對各城市配送區域進行重新規劃。

實驗目標：降低運單超出配送區域範圍佔比，提高配送效率。

實驗指標：

• 目標指標：xxxx；
• 護欄指標：xxxx。

實驗難點及約束：

• 策略和產品的特殊性：配送區域優化策略考慮在保障整體覆蓋範圍不變且區域之間不重疊的約束下，對加盟區域進行邊界優化甚至合併，然而對於2個相鄰的區域，在該約束下，優化A區域邊界必然會導致B邊界跟隨變化，因此從產品形態上無法實現A區域邊界變更但B區域邊界維持不變，此時不能考慮按區域隨機分流。這種情況下可以考慮將城市劃分為兩個半城，在實驗半城內部調整優化區域邊界，對照半城維持不變。

實驗方案：考慮到實驗難點及約束，採用半城平行趨勢分組，並使用雙重差分法進行評估。

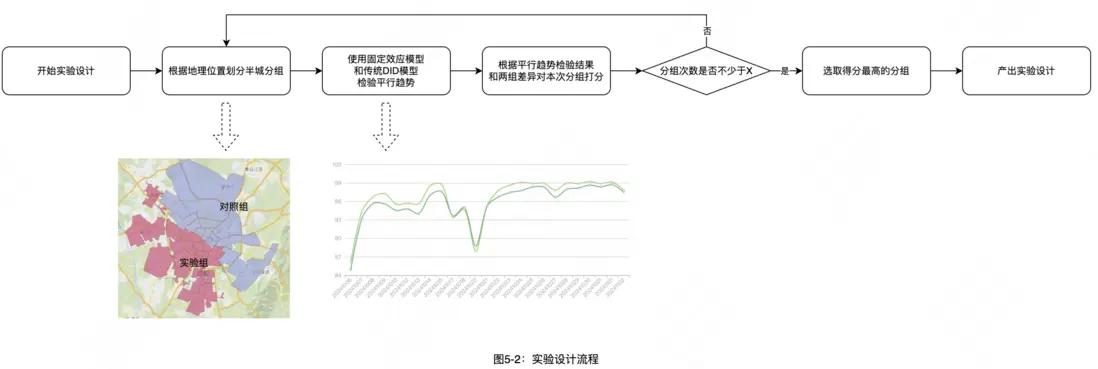
實驗設計：採用半城劃分+平行趨勢檢驗的實驗設計機制，對城市中配送區域進行分組，詳細流程可見圖5-2：

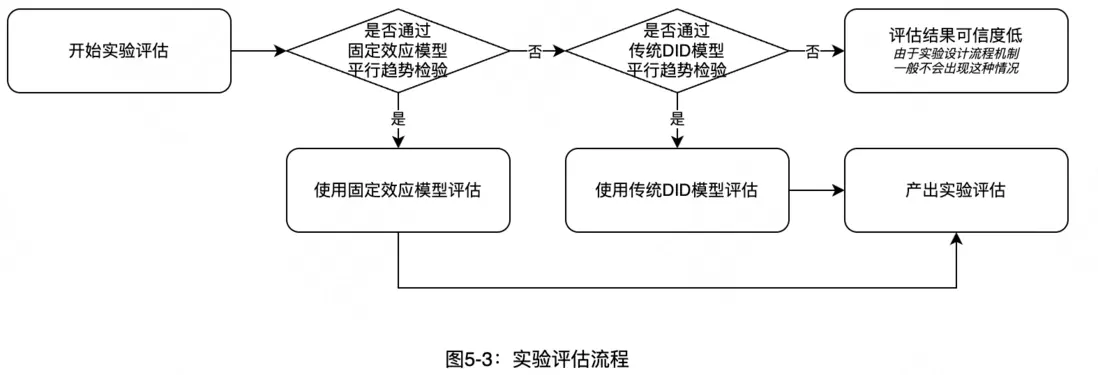
實驗評估：根據實驗前通過哪個模型的平行趨勢檢驗來決定用哪個模型來評估實驗後策略效果，詳細流程可見圖5-3，評估結果以下表為例：

5.2 拓展與展望

5.2.1 雙重差分法拓展

在傳統DID模型設定中，一個隱含假設是，實驗組的所有個體開始實驗的時間均相同。但有時我們也會遇到每個個體的實驗時間不完全一致的情形（Staggered Timing），比如有的實驗經過逐步放量，一部分個體從實驗第1天就開始接受策略處理，而另一部分個體則等到放量之後，第8天才開始接受策略。這時我們就可以用多時點DID模型來同時考察多次實驗的效果，模型設定如下：

在實踐中當出現平行趨勢不成立的情況時（建議儘量在實驗設計上採取更合理的分組，如果現實中已經結束實驗並平行趨勢檢驗表明假設不合理時），通常可以嘗試如下做法：

1. 放寬平行趨勢假設：例如學界的Honest DID為一種在平行趨勢假設可能不成立的前提下，進行穩健推斷（Robust Inference）和敏感性分析（Sensitivity Analysis）的方法。與直接假設平行趨勢成立不同，Honest DID允許實驗後平行趨勢的違背，但是限制違背程度與實驗前趨勢（pre-trends）的違背並不存在太大差異或至少有跡可循。
2. 條件平行趨勢假設：通過匹配等方法尋找滿足平行趨勢的羣體，例如基於實驗羣體PSM匹配合適的對照組羣體，再應用DID進行評估等。
3. 三重差分法：在雙重差分基礎上引入第三個差異維度（不受干預影響）更精確評估政策或干預措施影響的計量經濟學方法，但也增加了數據需求和模型複雜性。

5.2.2 其他準實驗方法

本文在準實驗上着重介紹了雙重差分法，此外還有一些斷點回歸、中斷時間序列等類準實驗方法可供讀者參考。

1. 斷點回歸（Regression Discontinuity Design, RDD）根據某個可觀測變量的閾值（斷點）劃分為實驗組和對照組，分析主要集中在斷點附近的樣本上。斷點附近可以認為有局部隨機性，即斷點附近的樣本是否受處置是隨機的，並且在是否處置之外的特徵上沒有系統性差異。
2. 中斷時間序列（Interrupted Time Series Analysis, ITSA）具體做法為在干預之前，使用不同時間的多次測量來創建一個模型（例如時間序列分析ARIMA模型），該模型可以估計干預介入後的相關指標的虛擬事實。干預後，再進行多次測量，並將關注指標的實際值和模型的預測值之間的平均差作為實驗效應的估計。當然中斷時間序列同樣可應用於多個實驗對象並且各個實驗對象可在不同時間點接受實驗干預（即設計上類似於多基線實驗）。此外簡單中斷時間序列的一種拓展是引入實驗變動然後將其反轉，並可以選擇多次重複此過程。

閲讀更多

| 關注「美團技術團隊」微信公眾號，在公眾號菜單欄對話框回覆【2024年貨】、【2023年貨】、【2022年貨】、【2021年貨】、【2020年貨】、【2019年貨】、【2018年貨】、【2017年貨】等關鍵詞，可查看美團技術團隊歷年技術文章合集。

| 本文系美團技術團隊出品，著作權歸屬美團。歡迎出於分享和交流等非商業目的轉載或使用本文內容，敬請註明 "內容轉載自美團技術團隊"。本文未經許可，不得進行商業性轉載或者使用。任何商用行為，請發送郵件至 tech@meituan.com 申請授權。