本文系《可信實驗白皮書》系列的第四篇文章,在上一篇我們將重點介紹隨機對照實驗相關的一些基礎知識,以及提高實驗功效的一些常見方法。本篇我們將圍繞隨機輪轉實驗展開,內容主要包括拋硬幣隨機輪轉、完全隨機輪轉、配對隨機輪轉等幾個實驗的介紹。
備註:本篇排版為圖文混合排版,如果想獲得更好的閲讀體驗,建議訪問「美團技術團隊」知乎官方賬號《可信實驗白皮書系列04:隨機輪轉實驗》。
時間片輪轉實驗(Switchback Experiment)是一種基於時間隨機化的實驗設計,其核心思想是將實驗單元在實驗時間段多次進行實驗組與對照組模式之間來回切換,通過比較某些指標在多時間段內實驗狀態與對照狀態的表現差異來檢測實驗效應。其被廣泛用於應對AB實驗中空間維度溢出效應(Spillover Effects)[1]干擾和樣本量不足的問題。
- 溢出效應:AB實驗的個體干預穩定性假設(SUTVA)假定實驗單元的結果不受到其他單元分組的影響,然而實際中由於實驗單元的直接關聯(社交網絡)或者間接關聯(共享資源等),使得無法保證實驗組與對照組個體之間彼此獨立,進而可能導致估計的實驗效應存在偏差,影響實驗結論的可信度。為解決這一問題,可考慮對同一個城市進行時間片輪轉實驗,例如在為期14天的實驗中,隨機分配7天為實驗組日期、7天為對照組日期,分別施加實驗策略、對照策略,以徹底消除空間溢出效應帶來的估計偏差。
- 樣本量不足:當隨機對照實驗樣本量存在不足時,例如,以單元A為實驗單位的隨機對照實驗功效不足,適當的結合時間片輪轉,採用實驗單元*時間片的分流輪轉實驗可在相同實驗時間內獲得更多的樣本量,進而提高實驗的效率。
由於上述特點,時間片輪轉實驗在履約場景中被廣泛應用,成為驗證履約業務策略的重要工具。然而,需要注意的是,輪轉實驗不適用於用户感知明顯的實驗策略,因為這可能會嚴重干擾用户的自然體驗。在下面章節中我們將重點介紹拋硬幣隨機輪轉、完全/分層隨機輪轉以及配對隨機輪轉實驗,更多輪轉實驗可詳見拓展與展望。
4.1 拋硬幣隨機輪轉
4.1.1 方法概述
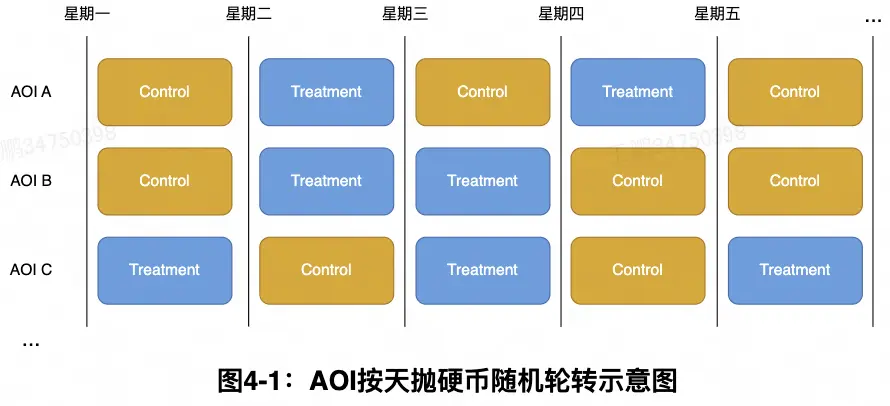
在普通的隨機分組實驗中經常會面臨樣本量不足的問題,這可能導致無法有效檢測出目標預期的提升效果。在這種情況下通常可以考慮加入時間片輪轉以增加獨立的樣本量,具體而言,可以採用實驗單元*時間片粒度的拋硬幣隨機輪轉實驗。在這種設計中,對於每個實驗單元i和時間片t,通過獨立的伯努利試驗隨機決定第i個實驗單元在第t個時間片分配到實驗組還是對照組。對於落在實驗組(對照組)的實驗單元i * 時間片t施加實驗策略(對照策略),最後通過對比實驗組和對照組的表現來估計策略的提升效果。拋硬幣隨機輪轉實驗設計比較簡單,通過加入時間片輪轉增加樣本量通常能夠顯著降低方差。但其不太適用於樣本量極少的場景(例如1個城市14天實驗週期下的全城按天輪轉實驗),由於在樣本量較少時容易出現實驗組與對照組樣本量差異明顯的情況,因此建議在獨立的實驗個體較多或者時間片較短時的情況下考慮使用這種方法。
4.1.2 分組機制
AOI按天拋硬幣輪轉實驗分組表達式示例
對照組分組表達式:(murmur332(murmur332(aoi_id, 隨機種子A)+murmur332(dt, 隨機種子B), 隨機種子C)%2) in (0)
實驗組分組表達式:(murmur332(murmur332(aoi_id, 隨機種子A)+murmur332(dt, 隨機種子B), 隨機種子C)%2) in (1)
4.1.3 評估原理
拋硬幣隨機輪轉實驗本質上與普通隨機對照實驗無差異,因此可直接引用第三章3.1.2普通隨機分組的評估方法。類似地,拋硬幣隨機輪轉實驗同樣可應用CUPED方法降方差,例如AOI*天拋硬幣隨機輪轉實驗選擇對應AOI實驗前對應周幾的數據作為協變量,如若是AOI*天*小時拋硬幣輪轉實驗選擇對應AOI實驗前對應周幾對應小時的數據作為協變量,以儘量提高實驗前後數據相關性,從而最大限度降低方差。
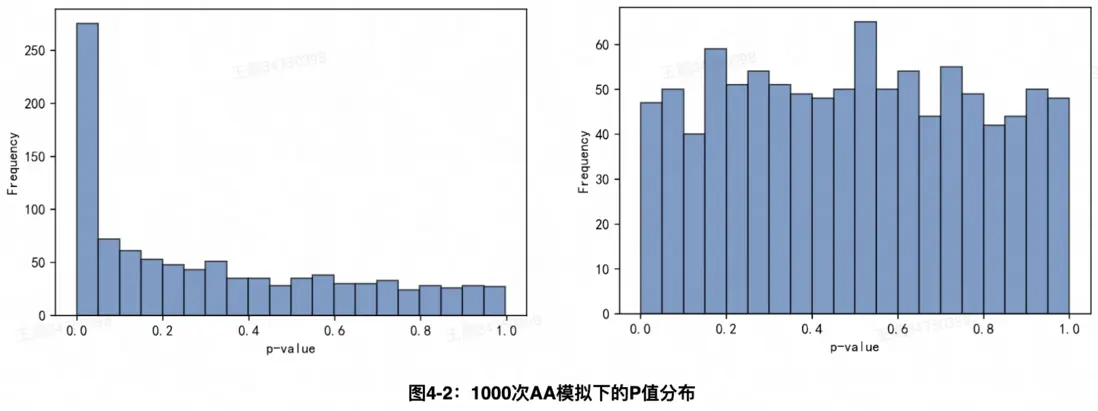
在使用拋硬幣輪轉實驗時,同樣需注意:實驗單元與分析單元不一致時,錯誤的方差計算方式容易低估方差,導致假陽性的問題。例如某實驗在分流時,將所有AOI分為兩部分,這兩部分AOI集合每天隨機分到實驗組或對照組,這時實驗單位是AOI集合*天,而實驗者評估時卻採用AOI*天粒度的數據計算方差,AOI集合下的AOI分組不獨立,若直接套用隨機化分組下的方差計算公式可能會導致低估方差,導致假陽性。如下圖4-2左圖所示,在策略沒有效果的情況下,誤判策略有效的概率超過25%。正確的計算方法是將實驗數據匯到AOI集合*天粒度計算方差,此時如圖4-2右圖P值近似服從均勻分佈,且假陽性的概率控制在5%以內。
4.2 完全隨機輪轉
4.2.1 方法概述
在全城存在強溢出效應,且小時級時間片輪轉存在攜帶效應的情況下,一種可行的做法是採用城市按天隨機輪轉實驗。例如在具有強LBS[3]業務屬性的履約實驗場景下,通常會存在溢出效應問題,超過1/3的履約實驗場景採用全城按天輪轉實驗。然而,由於實驗週期有限,城市按天輪轉實驗設計下的樣本量(即某個城市的實驗天數)通常較少。在這種情況下,若採用拋硬幣方式進行輪轉分組可能導致實驗組和對照組天數不平衡,例如14天的實驗可能出現5天實驗組和9天對照組的情況。這種不平衡通常不符合業務方對實驗狀態和對照狀態天數相等或相近的預期,某組天數非常少時也很難準確反映策略的效果,並可能損失實驗檢測功效。因此,在設計全城按天輪轉實驗時,通常需要特別注意組間天數的平衡,以確保實驗結果的可靠性和有效性。
完全隨機輪轉分組為整城按天輪轉實驗提供了一種合適的實驗設計,並具備科學的因果推斷評估理論。其通常可在實驗前的實驗設計階段,預先指定或固定實驗組和對照組的天數,從而實現實驗組和對照組天數相等或接近,甚至按需指定實驗狀態天數等。例如,在14天的按天輪轉實驗中,完全隨機輪轉允許指定恰好分配X天進入實驗組,剩下的14-X天進入對照組(例如X=7)。在此基礎上,可進一步結合分層技術進行分層完全隨機輪轉,即先按照某些特徵屬性劃分為多個層/類,再在每層分別採用完全隨機輪轉。例如為期14天實驗中,按照是否週末分層,在10個工作日中隨機分配5天作為實驗組、5天作為對照組,4個週末日期隨機分配2天為實驗組、2天為對照組。類似地,對於多個實驗城市,可考慮按城市分層,在每個層(即城市)內應用完全隨機輪轉,以提高實驗組和對照組的同質性。
4.2.2 分組機制
例如,如果實驗週期內共有4個週末天數,可以確保2天分配到實驗組,另外2天分配到對照組,以此控制因週中和週末差異引起的潛在偏差,從而提高實驗結果的準確性。在涉及多個城市的按天輪轉實驗時,建議按城市進行分層,並在每個城市內分別採用完全隨機輪轉。通過此方案確保每個城市實驗組和對照組的同質性,同時可降低因城市之間差異帶來的方差,提高檢驗靈敏度。
4.2.3 評估原理
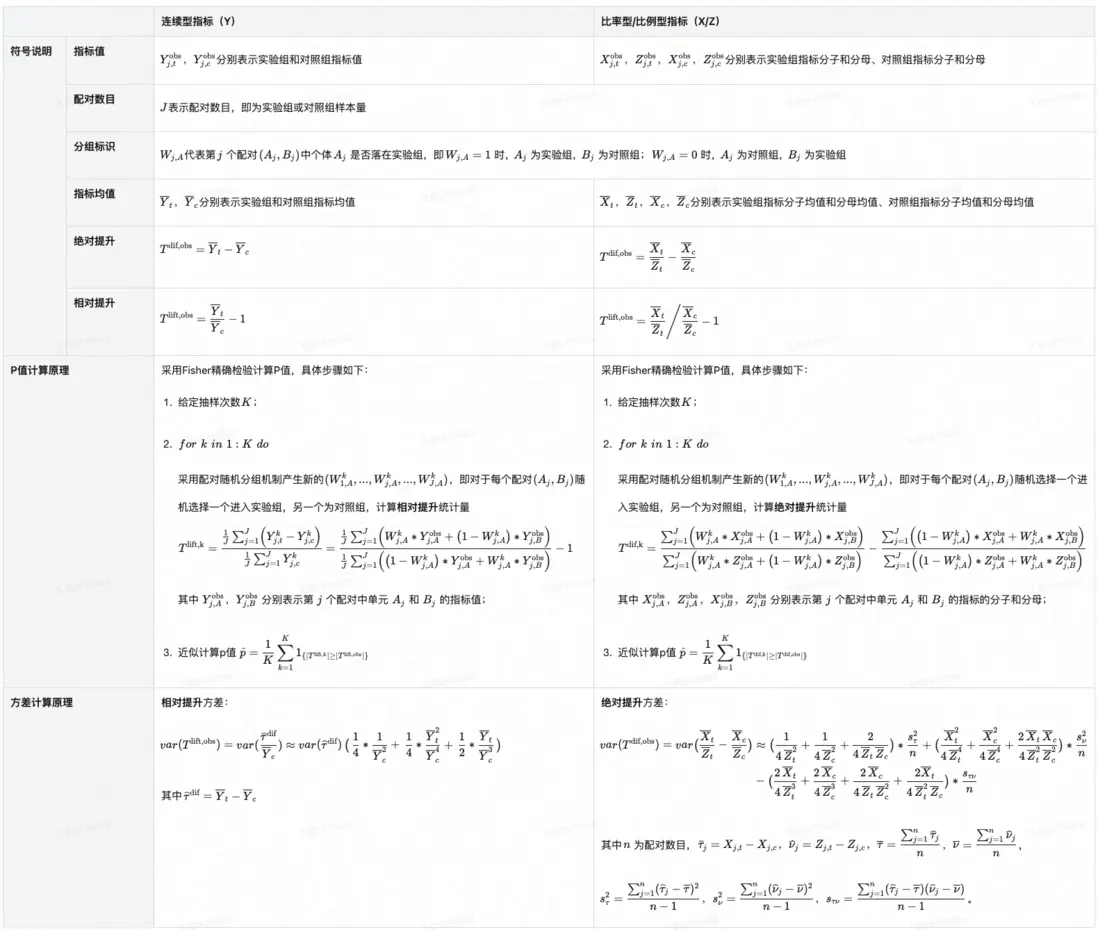
考慮到完全隨機輪轉分組通常在樣本量較小時應用,在評估時建議採用非參Fisher精確檢驗計算$p$值,Neyman方法計算方差/MDE(Fisher無法計算方差等),具體計算邏輯如下表所示:
4.2.4 分層隨機輪轉
4.3 配對隨機輪轉
4.3.1 方法概述
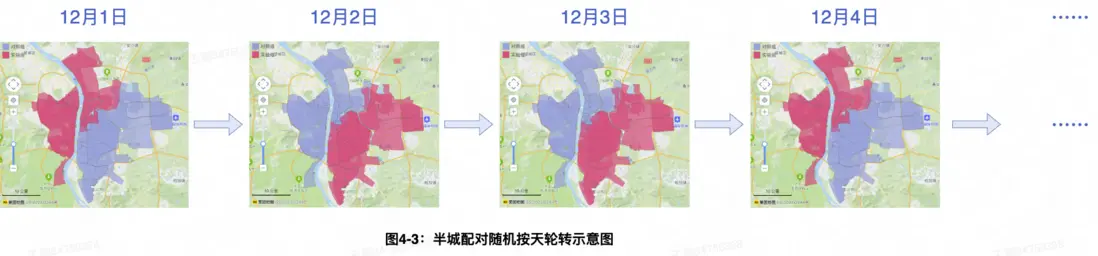
為避免溢出效應而採用城市按天完全隨機輪轉實驗時,由於實驗組和對照組處於不同天,若天之間存在較大差異時,往往會導致樣本數據波動較大,難以檢測出策略效果。此時一種可行的做法是採用半城配對隨機輪轉實驗,具體來説,可以事先將整個城市按照地理位置和其它相關特徵劃分為兩個特徵足夠相似的半城[4],記為(半城A,半城B),然後每天隨機選擇一個半城進入實驗組,另一個半城作為對照組。例如第一天隨機分配半城A為實驗組,半城B為對照組;第二天再進行類似的隨機分配。
在此實驗設計下,同一城市中的實驗組和對照組每天同時存在,相似的兩個半城控制天之間差異對實驗組和對照組的影響是相似的,從而有效減少隨機誤差。加之配套的配對評估理論,配對輪轉實驗通常可顯著提升實驗檢測靈敏度。然而,由於半城配對輪轉在空間上無法完全隔離實驗組和對照組,仍可能存在輕微的溢出效應(主要在兩個半城交界處)。與全城按天隨機輪轉相比,半城配對按天隨機輪轉實際上是通過接受一定的溢出效應偏差來換取更小的隨機誤差。當隨機誤差大於溢出效應帶來的偏差時,這種實驗設計能夠提供更精確的結果。
4.3.2 分組機制
配對的設計旨在控制實驗組和對照組之間的差異,從而減少混雜變量的影響。配對隨機輪轉實驗在配對隨機基礎上引入了時間片輪轉機制,使得每個個體都有機會進入實驗組或對照組,從而進一步控制潛在的混雜變量。對於履約最常用的半城配對隨機按天輪轉實驗,如圖4-3所示,其將整個城市基於地理位置和其它相關特徵(協變量)劃分為兩個特徵相似的半城,即每天兩個半城為一對,每天隨機選擇一個半城分配到實驗組,另一個半城到對照組。
4.3.3 評估原理
配對隨機輪轉實驗和配對隨機實驗使用相同的評估方法,採用Fisher精確檢驗計算P值,Neyman方法計算方差,具體計算邏輯如下表:
4.4 拓展與展望
4.4.1 異常場景處理
在按天輪轉實驗中,若實驗期間出現突發性外部干擾,可能導致指標波動劇烈,影響策略效果的檢測。針對此類場景,可根據實際需求選擇以下處理方式。
方式1:異常值剔除
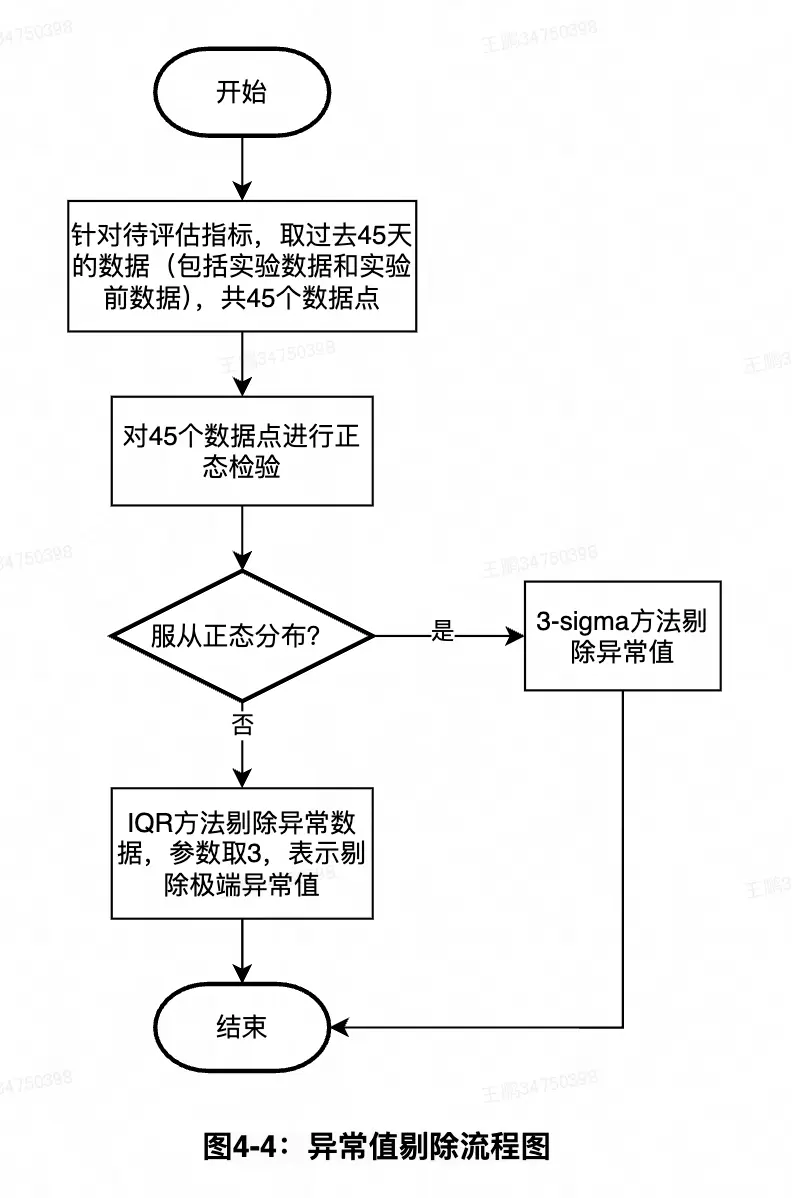
對於非目標場景或無需關注特定干擾下策略效果的情況,可採用異常值剔除方法。支持自定義業務場景中反映異常狀態的指標,通過統計分析識別並剔除異常值。若選擇多指標,則對每個指標剔除的天數取並集。具體流程如下:
① 取過去45天[5]的數據來進行正態性檢驗,並用於估計3-sigma準則中的方差和IQR準則中的分位點,以此為依據進行實驗數據的剔除。
② 當數據的正態性較好時,採用常用的3-sigma方法;當數據正態性較差時,通常會出現厚尾情況,這時採用更為激進的IQR方法來進行剔除。
方式2:協方差分析+CRSE
對於需評估特定干擾場景下策略效果的情況,直接剔除數據可能引入偏誤,此時可考慮採用協方差分析的方法消除混雜因素對分析指標的影響。協方差分析是用於在檢驗兩組或多組修正均數之間有無差異時,消除混雜因素對於分析指標影響的一種分析方法。例如某實驗採用城市按天完全隨機輪轉設計,因突發性外部干擾導致指標波動較大,這時可以以運單為個體建立迴歸模型,在模型中加入環境干擾等級作為協變量,以消除混雜因素影響。
由於實驗採用全城按天輪轉的方式,同一城市同一天的運單可能是相關的,導致模型的誤差項之間可能相關,這時使用普通最小二乘法(Ordinary Least Squares,OLS)估計的標準誤是有偏的。為了解決這一問題,可以使用CRSE(Cluster Robust Standard Error,聚類調整標準誤),放寬獨立同分布的假設,允許組內個體存在相關性,不同組之間個體彼此不相關,將分流維度(即城市*天)作為Cluster來評估策略效果。
4.4.2 小時級輪轉下的攜帶效應
需要特別注意的是,儘管時間片粒度越細在實驗總時長不變情況下樣本量越大,通常可帶來實驗功效的提升。然而由於時間維度的相依性往往會導致細粒度時間片的輪轉實驗中存在攜帶效應,即上一時刻策略會影響下一時刻的表現。例如,在交通信號燈優化實驗中,假設某路口每十分鐘切換一次綠燈時長策略以優化車輛通行效率。若前一時間片採用縮短綠燈時長的策略(如綠燈30秒),可能導致車輛排隊積壓;即使下一時間片恢復為原有時長(綠燈60秒),積壓的車輛仍需額外時間疏散,此時通行效率指標(如平均等待時長)仍受前一階段策略的滯後影響。
這種跨時間片的策略干擾會導致因果效應估計偏誤,影響實驗結論的準確性。這時需要科學的方法消除攜帶效應的影響。目前對連續型指標的攜帶效應估計模型已在履約有所應用,但對於履約場景最常見的比率型指標下的攜帶效應估計還未有落地方案。
經過對學業界理論方案的調研,對於攜帶效應,通常有以下三種解決思路:① 利用模型估計攜帶效應並輔助調整消除真實效果偏差;② 利用消除時長(wash-out/burn-in period)去除攜帶效應的影響;③ 利用時間序列模型進行優化設計。
上述的三種方案均具有一定的侷限性,儘管方案①易於操作,但在實際問題中可能存在模型錯誤等問題,影響評估效果。其次,由於模型中包含攜帶效應,對於攜帶效應的估計也會影響處理效應的估計精度。因此方案①並不是一種最為理想的分析方案。相較於方案①,方案②不依賴於模型,因此更加穩健,但需要預估攜帶效應影響時長以構建合理的分配時長。在分析數據的過程中,方案②還需利用消除時長去除受攜帶效應影響的部分數據,再對處理效應進行估計,以此實現消除攜帶效應。然而,目前對於如何預估攜帶效應時長,以及如何確定消除時長尚無明確的解決方案。
此外,方案②未能將數據的時間序列特徵納入考慮,因此儘管方案②具有一定的優越性,但仍不能保證該方案能較好的降低估計的方差。方案③考慮從數據的時間序列特徵出發,將時間序列模型與因果推斷問題結合,利用最優實驗設計的想法提升處理效應的估計精度和檢驗功效。目前,該方案僅考慮了ARMA(p,q)模型,因此對於實際問題中可能存在的非平穩過程並不完全適用。因此儘管已線下落地上述部分方法,但如何針對美團的履約問題開發最合理的按小時輪轉實驗方案還有待進一步的研究。我們已通過校企合作,針對美團的業務場景開展研究,為美團履約平台開發具有優良性質的按小時輪轉實驗以減小攜帶效應以及時間混淆效應的影響。
4.4.3 其他輪轉實驗設計
交替輪轉實驗是另一類重要的時間片輪轉實驗設計,其特點是在連續的時間片中交替分配實驗組和對照組,例如上一時間片為實驗組,下一時間片為對照組,再下一時間片為實驗組這種交替改變分組的方式。通常而言這種實驗設計往往更符合實際業務訴求,尤其是在每天的各時間片具有明顯週期性且各時間片差異顯著的場景下。然而,在評估方面(尤其是p值計算)通常需要模型/條件假設,這對評估的科學性具有一些挑戰。
例如,業界的一些應用案例,DoorDash在評估廣告效果時採用按天的時間片交替輪轉實驗,通過使用歷史數據+Bootstrap抽樣來近似構造統計量在原假設下的分佈,從而進行t檢驗,但該方式需要假設歷史基線與實驗期間保持一致。
國內某互聯網公司考慮小時級交替輪轉實驗,並在評估時引入未考慮攜帶效應的VCM(Varying Coefficient Model)模型,或者考慮攜帶效應的VCDP(Varying Coefficient Decision Process)模型,由於理論細節較多,暫不在此做詳細介紹,感興趣的讀者可以進一步查閲相關文獻。
但需要注意的是,按天交替輪轉實驗的分組機制是比較偏向於非隨機的:一旦確定實驗開始的第一天屬於實驗組或對照組,後續天的分組將相繼確認。這時如果實驗者採用完全隨機輪轉實驗等方法計算方差,忽略分配機制可能導致方差計算的錯誤。此外,交替輪轉基於某些假設的建模分析,通常需要較大的樣本,在按天輪轉樣本量較少的場景下通常不適用。
解釋説明
- [1] 溢出效應(Spillover Effects):AB實驗中關鍵的個體干預穩定性假設(SUTVA)假定實驗單元的結果不受到其他單元分組的影響,然而實踐中由於實驗單元間的直接關聯(社交網絡)或者間接關聯(競爭共享資源等),參與AB實驗的實驗組與對照組之間可能並不獨立,我們通常稱實驗組、對照組間的干擾影響為溢出效應。
- [2] 攜帶效應(Carryover Effect):可理解為時間維度的溢出,指某一時刻的策略效果或影響延續到後續時刻,影響後續時刻的策略或效果。攜帶效應的階為m代表時刻t最多會影響t+m時刻的結果,不會影響更後時刻的潛在結果。
- [3] LBS:Location-Based Services,基於位置的服務
- [4] 半城:半城在此是指同一個城市中由地理位置相鄰的具有經緯度信息的單元(例如配送區域、AOI等)組成的集合。
- [5] 45天:45天的考慮在於,歷史數據的時間跨度不應取的太長,因為不同季節的異常天氣影響可能差別較大,較久前的數據刻畫跟當前季節的實際情況有差距;同時天數不應取的太少,否則會導致正態性檢驗,方差和分位點估計的不準確。
| 關注「美團技術團隊」微信公眾號,在公眾號菜單欄對話框回覆【2024 年貨】、【2023 年貨】、【2023 年貨】、【2022 年貨】、【2021 年貨】、【2020 年貨】、【2019 年貨】、【2018 年貨】、【2017 年貨】等關鍵詞,可查看美團技術團隊歷年技術文章合集。
| 本文系美團技術團隊出品,著作權歸屬美團。歡迎出於分享和交流等非商業目的轉載或使用本文內容,敬請註明 "內容轉載自美團技術團隊"。本文未經許可,不得進行商業性轉載或者使用。任何商用行為,請發送郵件至 tech@meituan.com 申請授權。