在上一篇文章中,我們詳細闡述了AB實驗的概念與其價值,並結合美團的實際情況,探討了AB實驗中常見的挑戰及建設經驗。本篇作為可信實驗白皮書系列的第二章,將重點講解AB實驗的理論原理及其背後的統計學基礎。
2.1 實驗基礎原理概述
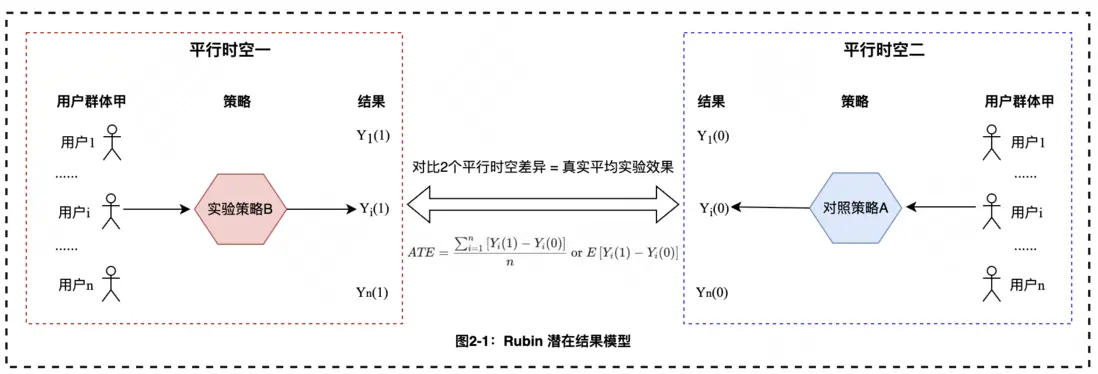
AB實驗原理源於統計學中經典的Rubin潛在結果模型(也稱反事實因果推斷框架)。考慮最簡單的情況,當我們想要比較兩個策略的差異以獲得更優策略時。如圖2-1所示,最理想的方案是面向同一撥用户或者全部用户,假設存在兩個完全相同的平行時空,平行時空一中所有用户體驗實驗策略B,類似的平行時空二中所有用户體驗對照策略A,那麼直接對比2個平行空間用户行為指標表現,則可決定哪個策略勝出以及觀測真實的平均實驗效應。
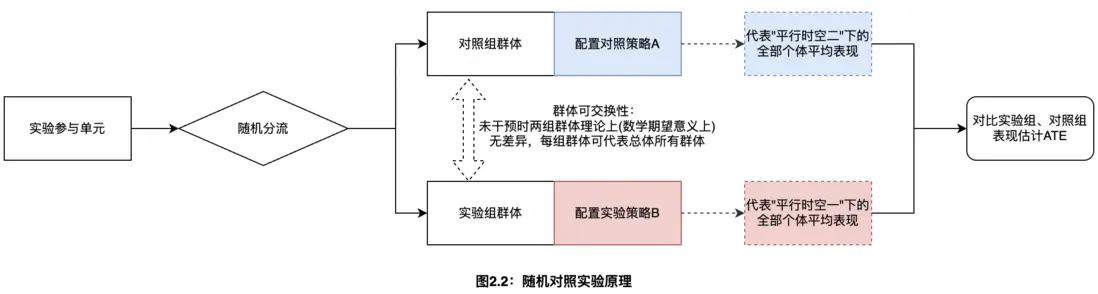
然而,現實世界中不存在兩個平行時空,針對同一用户,我們只能觀察到其接受策略A或策略B下的一種表現。因此,現實世界中通常考慮先通過隨機實驗手段,將用户隨機均勻地分為實驗組和對照組2個足夠相似的羣體,並分別施加實驗策略B以及對照策略A。
如圖2.2所示,在這種隨機分配下理論上實驗組和對照組用户的平均表現(在數學期望意義下)可以分別代表2個平行時空下所有用户的平均表現,因此通過對比實驗組、對照組間差異可以有效估計策略迭代帶來的具體收益、風險與成本,幫助實驗組精細成本收益,結合業務做出更為理性的決策。然而在單次實驗中,儘管理論上實驗組和對照組來自同一總體,但實際上每次隨機分配下2組間業務指標通常存在一定的差異(樣本量越多差異越小)。這種差異可以理解為由抽樣機制或者是分組機制的隨機性貢獻,即每次隨機分配下實驗組、對照組個體未施加策略時的平均差異在真值0附近波動。為準確識別單次AB實驗中兩組差異觀測值是由分組的隨機波動還是真實策略效果貢獻,通常需藉助假設檢驗、置信區間等統計工具進行判斷和論證(相關內容可參考2.2章節)。
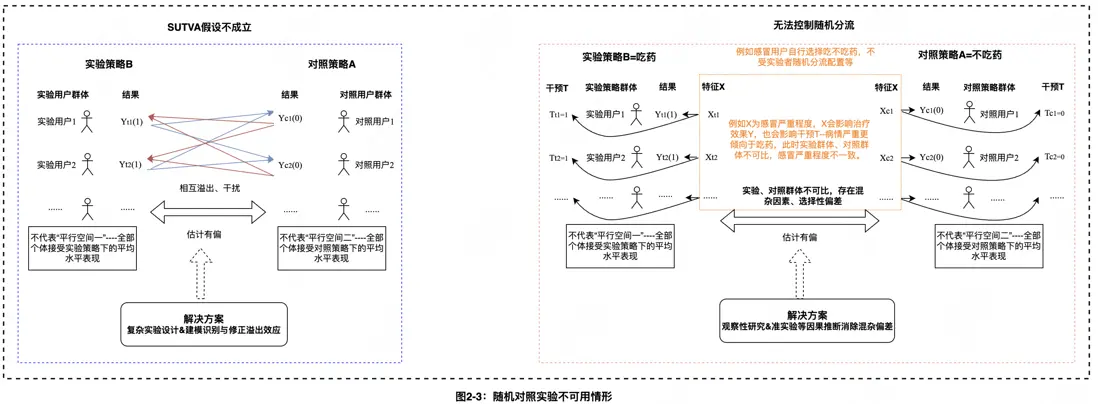
然而,隨機對照實驗準確刻畫策略因果效應存在2大關鍵前提:
- 個體處理穩定性假設(SUTVA):實驗單元的行為結果不受到其他單元分組的影響,即實驗單元間相對獨立,不會因為直接關聯(如社交網絡)或者間接關聯(如共享資源)而互相產生干擾或者溢出。SUTVA被破壞的典例包括:某打車App想要測試不同的溢價算法時,如果效果很好以至於實驗組乘客更願意打車,則路上可供搭乘的司機數量會減少,進而可能導致對照組難打上車,從而打車的對照乘客減少。又例如某通信工具上線增加通話時長的新功能時,如果實驗組用户通話時長增加,而實驗用户通話對象包括對照用户,從而也會提高對照組用户的通話時長。(信息源自:Ron Kohavi, Diane Tang, Ya Xu 著作《關鍵迭代--可信賴的線上對照實驗》)
- 分組隨機性:實驗單元進入實驗組、對照組可完全由實驗者隨機分配,不受限於實驗單元自身行為選擇與表現。分組隨機性破壞的案例包括例如在測試吃藥是否對治療感冒有效時,吃藥行為可能完全由病人自行決定,且感冒更嚴重的人更加偏向於吃藥,而不是隨機選擇。SUTVA假設以及分組隨機性的破壞會導致實驗組(對照組)平均表現並不代表平行空間一(平行空間二)---全部個體接受實驗(對照)策略下的平均表現,因此對比實驗羣體與對照羣體的表現不能準確反映策略的真實效果。需引入更高階實驗方法或因果推斷技術來解決,詳情請參閲後面章節。
2.2 AB實驗統計學基礎
2.2.1 參數估計
參數估計是數理統計中通過樣本數據推斷或估計總體未知參數的基本方法,在眾多實際領域中被廣泛應用。例如基於某批產品的隨機抽樣檢查結果來估計總體廢品率;又或者在AB實驗中基於實驗組、對照組樣本表現差異去估計真實策略提升效果。大體而言,參數估計可劃分為兩大類:點估計和區間估計。
點估計(Point Estimation)
點估計,簡而言之是使用樣本數據計算一個單一的數值來估計總體參數。例如為了調查某批產品的廢品率c,可以從該批產品中隨機抽取n個產品進行檢查,記a為檢查產品中為廢品的個數,則可考慮用a/n估計總體廢品率c。常用的構造點估計的方法包括矩估計、極大似然估計、貝葉斯估計等,在此不詳細展開介紹。點估計作為明確告知“未知參數是多少”的基本手段,那麼現實中怎麼評估點估計準不準?進一步的對於同一參數,不同估計方法求出的估計量可能不一樣,那麼如何判斷不同的估計量之間的優劣。相合性、無偏性和有效性是常用的3個標準。相合性指當樣本量無限增加時,點估計值趨近於總體參數值,即大樣本下估計量能夠準確反映總體參數。無偏性指從樣本中得到的估計量的期望與總體參數相等,而有效性則指在樣本量相同情況下,點估計A方差<點估計B方差則代表估計量A更有效。
從上式中不難看出一個好的估計需要滿足無偏性或者漸進無偏性,即偏差Bias等於0或者隨着樣本量增加趨於0。與此同時在無偏條件下方差越小則點估計與參數真值越接近。通常而言,基於極大似然估計等方法構造的點估計的方差項Var通常以1/n階速度趨於0,其中n為樣本量。
回到AB實驗,實驗者通常感興趣策略總體提升效果ATE,旨在通過實驗收集樣本構造 ATE的點估計。在SUTVA假設成立的隨機對照實驗下直接對比實驗組、對照組表現的點估計滿足相合性和無偏性/漸進無偏性,並且隨着樣本量的增長點估計值趨近於總體參數值,因為方差(抽樣/分組隨機性貢獻)隨着樣本量增加也趨向於0。然而對於SUTVA假設以及分組隨機性的破壞,會導致偏差Bias存在或者説不收斂到0。因此此時需要一些複雜實驗設計、建模分析與因果推斷技術着重消除、避免偏差項,從而保證點估計的準確性。
置信區間(Confidence Interval)
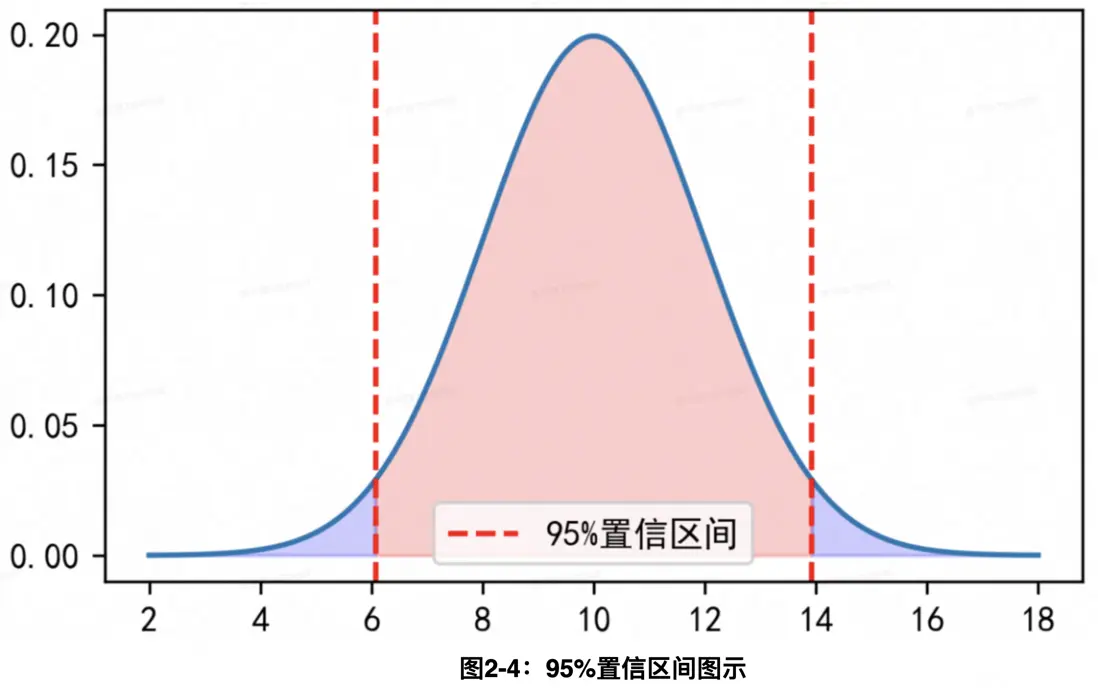
對於總體的未知參數,在有限樣本下點估計總存在一定的波動或誤差,一個取而代之的自然想法為:兼顧波動性考慮估計參數落在哪個區間範圍內,這便是統計學中經典的置信區間模塊。置信區間顧名思義指的是總體參數的一個區間估計,以95%置信區間[a,b]為例,其表明區間[a,b]包含參數真值的概率在95%左右。例如假設我們要估計某城市中所有居民的平均收入。我們從這個城市中隨機抽取了一部分樣本,並計算了95%的置信區間結果為[5000元, 7000元]。這意味着我們有95%的信心認為,整個城市中所有居民的平均收入在5000元到7000元之間。又例如在對比新App頁面設計與舊頁面設計AB實驗中,考慮到單次實驗下隨機分組波動性,轉化率提升值點估計0.03與真實效果理論值存在一定的波動,此時可進一步參考95%置信區間估計[−0.00136,0.06136],即判斷置信區間[−0.00136,0.06136]包含真實策略效果理論值的把握在95%以上,或者説有95%以上信心判斷真實提升效果在−0.00136~0.06136之間。通常而言在置信水平固定情況下區間長度越短越好,學業界最經典的95%置信區間構造方式為$\widehat{\theta} \pm 1.96*\sqrt{Var(\widehat{\theta})}$,即在點估計基礎上增加一個波動範圍。從置信區間構造形式上也不難看出隨着樣本量的不斷增加,置信區間變得越來越窄並收斂到參數真值點。
2.2.2 假設檢驗
假設檢驗(Hypothesis testing)是統計學中用數據論證某假設是否成立的方法,在工程、醫學、社會科學等多個領域廣泛應用。假設檢驗本質可理解為反證法,有點類似於法庭的評理,想象法庭上有一名被告,在開始無信息時假設被告是清白的(原假設),而檢察官必須要提出足夠的證據去證明被告的確有罪。如果沒有足夠的信息和證據證明被告有罪,那麼判定原假設:被告清白成立。除非檢察官提供足夠的證據才判定被告有罪。統計學家Fisher提過一個女士品茶的假設檢驗著名例子,一名女士聲稱其可以品嚐出奶茶製作過程中是先加入茶還是先加入牛奶。Fisher提議給她八杯奶茶,並告知其中四杯先加茶,四杯先加牛奶,但隨機排列,需要女士説出這八杯奶茶中,哪些先加牛奶,哪些先加茶。原假設是該女士無法判斷奶茶中的茶先加入還是牛奶先加入,根據猜中的次數判斷該假設是否成立。結果女士測試結果為八杯品嚐都正確。在原假設下若單純以概率考慮,八杯都正確的概率為1/70(因為8選4的組合數是70),約1.43%,即原假設成立下統計上完全猜對可能性極小,單次測試基本上不會發生,即幾乎排除女士完全盲猜正確的可能,因此我們有理由去拒絕“該女士無法判斷奶茶中的茶先加入還是牛奶先加入”的假設。
類似的,假設檢驗在AB實驗中通常被作為基本工具論證新策略是否相對舊策略會帶來業務收益。例如當測試一個新的App廣告設計是否能提高用户點擊率時,通常原假設新策略相對舊策略無效,然後收集現有證據--樣本數據去論證實驗組和對照組之間是否具有顯著的差異,如果擁有足夠證據——實驗組對照組差異很大(這在新策略無效下基本上不太可能出現),則推翻“新策略相對舊策略無效”的假設,否則認為在現有證據——樣本信息下接受原假設成立,除非收集更多證據(樣本數據)再“重新開庭論證”。一個完整的假設檢驗主要包括以下幾個步驟:
1.提出假設
- 原假設(Null Hypothesis,通常選擇為默認結論或者需推翻的結論)H0:實驗組與對照組無差異,表示策略無效果。
- 備擇假設(Alternative Hypothesis,通常為想被證明的結論)H1:實驗組與對照組有差異,也可考慮單邊備擇假設H1:實驗組>對照組,或者H1:實驗組<對照組。但在AB實驗中為同時兼顧收益和風險通常默認選擇雙邊備擇假設。
2.選擇顯著性水平
顯著性水平(α)指能容忍的犯第一類錯誤的概率,其中第一類錯誤是指在原假設為真時,拒絕原假設的犯錯,又稱假陽性。顯著性水平是人為定義或指定的概率值,學業界常見的顯著性水平為0.05。
3.構造檢驗統計量
根據樣本數據和假設類型,選擇合適的檢驗統計量,AB實驗中最常用的方式為雙樣本t檢驗。例如在探索某策略是否會帶來單量增長時,按用户隨機對照試驗可考慮構造檢驗統計量:
其中方差計算常用算法包括Delta方法、Bootstrap、Jackknife方法等,當然檢驗方式也包括參數檢驗、非參數檢驗等。
4.計算拒絕域和p值
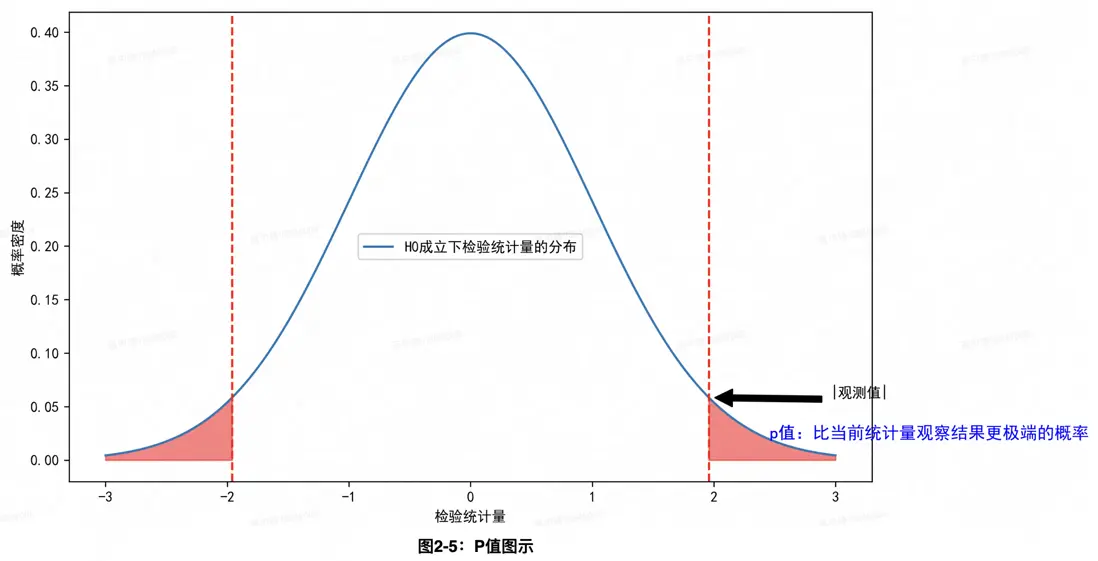
拒絕域是指在假設檢驗中拒絕原假設的檢驗統計量的取值範圍,其通常依賴於顯著性水平等。儘管可通過判斷檢驗統計量觀測值是否落在拒絕域決策拒絕/接受原假設,假設檢驗實際應用中通常考慮一個更常用的標準——P值。P值表示在原假設為真時,比所得到的統計量觀察結果更極端的概率。其計算邏輯為先推導出在原假設H0成立條件下檢驗統計量的概率分佈(在AB實驗場景可以想象為,在策略無效場景下,假設允許做無數次實驗,每次實驗獨立執行分組機制,並且得到一個檢驗統計量,基於若干次實驗得到的若干個檢驗統計量觀測值畫圖,即得到H0下且在對應實驗分組機制下的檢驗統計量的概率分佈。現實中可通過一些極限理論等統計定理性質來基本近似獲得原假設H0成立條件下檢驗統計量的概率分佈),然後再計算觀察到比當前樣本下檢驗統計量觀測值更極端的概率,直觀上也可理解為在原假設成立情況下,出現當前觀測值及更極端場景的概率,如果很小則意味着原假設成立下單次實驗不太能出現的小概率事件發生了,需質疑甚至拒絕原假設。
5.作出決策
假設檢驗的核心思想反證法,理論上小概率事件在一次實驗中幾乎不可能發生,如果發生了則説明原假設不合理。因此可通過比較p值與顯著性水平α:
- 如果p值 ≤ α,拒絕原假設,支持備擇假設。
- 如果p值 > α,接受原假設,拒絕備擇假設。
2.2.3 極限理論
極限理論是假設檢驗與置信區間等過程中構建統計量分佈的理論基礎,是統計學中一個龐大且內容豐富的關鍵模塊。由於主題和篇幅的限制,本白皮書將不對其進行深入探討,僅簡要介紹幾個常用的原理。讀者也可選擇跳過本部分內容。
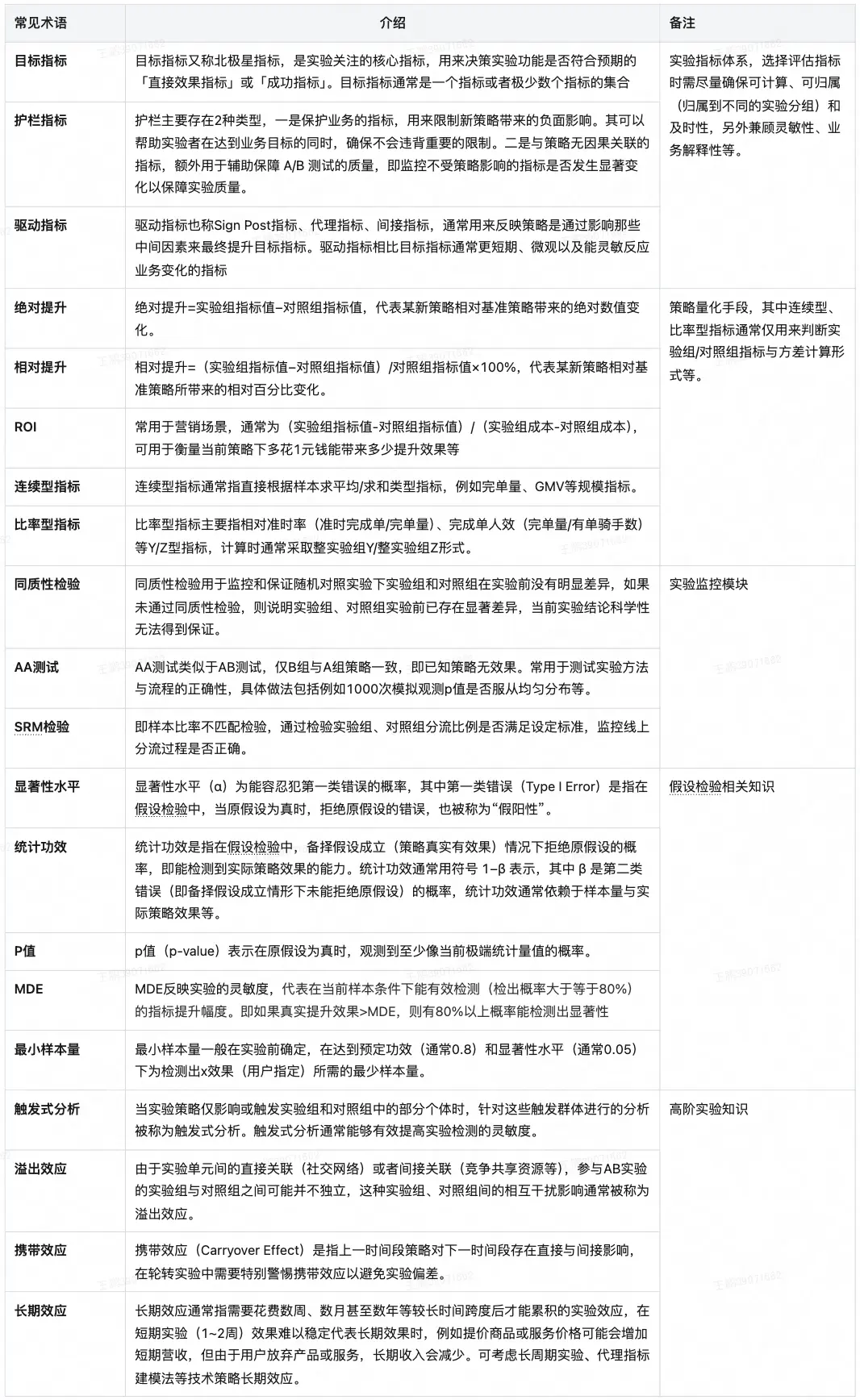
2.3 常用實驗術語
寫在後面
後續,我們將在美團技術團隊微信公眾號上陸續推出第3章節~第8章節的內容,敬請期待。如果大家發現問題,或者有一些建議,也歡迎在文末留言,跟我們進行交流。
閲讀更多
| 關注「美團技術團隊」微信公眾號,在公眾號菜單欄對話框回覆【2024 年貨】、【2023 年貨】、【2023 年貨】、【2022 年貨】、【2021 年貨】、【2020 年貨】、【2019 年貨】、【2018 年貨】、【2017 年貨】等關鍵詞,可查看美團技術團隊歷年技術文章合集。
| 本文系美團技術團隊出品,著作權歸屬美團。歡迎出於分享和交流等非商業目的轉載或使用本文內容,敬請註明 "內容轉載自美團技術團隊"。本文未經許可,不得進行商業性轉載或者使用。任何商用行為,請發送郵件至 tech@meituan.com 申請授權。