二叉樹的基本套路我們已經很熟悉了,接下來我們聊聊二叉樹的遞歸套路,可以解決面試中絕大多數的二叉樹問題,尤其是樹型dp問題,其本質是利用遞歸遍歷二叉樹的便利性。
判斷二叉樹是否是完全二叉樹
1、經典寫法思路
(1)某個節點有右孩子無左孩子,則一定不是完全二叉樹
(2)當第一次遇到左右孩子不雙全的節點時,以後遇到的節點都是葉節點
2、遞歸套路思路
對於任意一顆子樹,判斷是否是完全二叉樹的條件(列出所有可能性)
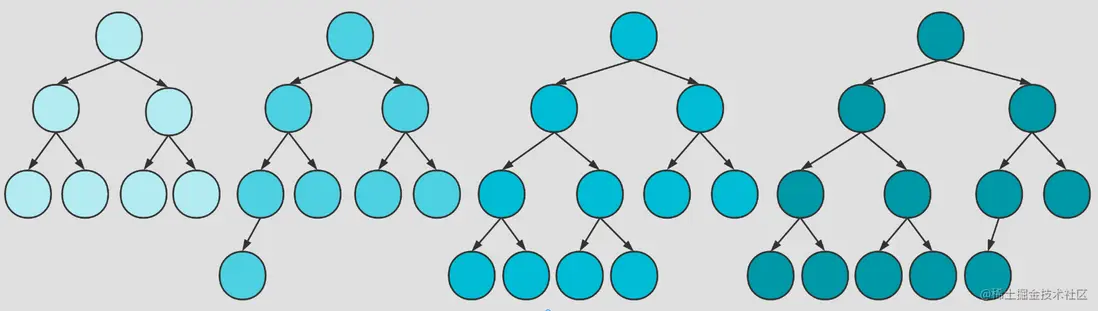
(1)左樹是滿的,右樹是滿的,左樹高度 = 右樹高度
(2)左樹是完全二叉樹,右樹是滿的,左樹高度 = 右樹高度 + 1
(3)左樹是滿的,右樹是滿的,左樹高度 = 右樹高度 + 1
(4)左樹是滿的,右樹是完全二叉樹,左樹高度 = 右樹高度
只有這4種情況二叉樹才可能是完全二叉樹(當然也可能是滿二叉樹,滿二叉樹本身也是完全二叉樹)
也就是每次從左子樹和右子樹中我們都需要 是否滿二叉樹、是否完全二叉樹、高度 三個數據,儘管我們最後只返回是否完全二叉樹,但是我們需要高度、是否滿來輔助我們判斷是否完全二叉樹,所以可以定義如下的Info類
public static class Info {
public boolean isFull;
public boolean isComplete;
public int height;
public Info(boolean isFull, boolean isComplete, int height) {
this.isFull = isFull;
this.isComplete = isComplete;
this.height = height;
}
}
3、遞歸套路代碼
(1)首先判斷為空時好不好設置,此時是好設置的,節點為空時new Info(true, true, 0),即認為空節點是滿二叉樹、是完全二叉樹、高度為0。
(2)然後根據列出的所有可能性,編寫遞歸套路的代碼,因為要整個形成遞歸,所以每一步都要返回Info類,不然咋遞歸下去呢?
此步的核心套路就以下三步:
1)無腦獲取左右子樹的Info信息
2)根據左右子樹拼湊自己的Info信息
3)返回自己的Info信息
/**
* @author Java和算法學習:週一
*/
public static Info process(Node x) {
if (x == null) {
return new Info(true, true, 0);
}
// 獲取左右子樹
Info leftInfo = process(x.left);
Info rightInfo = process(x.right);
// 拼湊自己的信息
boolean isFull = leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height;
boolean isComplete = false;
if (leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height) {
// 左滿,右滿,高度相等
isComplete = true;
} else if (leftInfo.isComplete && rightInfo.isFull && leftInfo.height == rightInfo.height + 1) {
// 左完全,右滿,高度差1
isComplete = true;
} else if (leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height + 1) {
// 左滿、右滿,高度差為1
isComplete = true;
} else if (leftInfo.isFull && rightInfo.isComplete && leftInfo.height == rightInfo.height) {
// 左滿、右完全,高度相等
isComplete = true;
}
// 左右子樹高度最大的加上自己的高度1,即是此節點的高度
int height = Math.max(leftInfo.height, rightInfo.height) + 1;
return new Info(isFull, isComplete, height);
}
(3)主函數調用遞歸方法獲取結果
/**
* 遞歸套路解法
*
* @author Java和算法學習:週一
*/
public static boolean isCompleteBinaryTree2(Node head) {
if (head == null) {
return true;
}
return process(head).isComplete;
}
所有代碼地址:
https://github.com/monday-pro...
判斷二叉樹是否是平衡二叉樹
平衡二叉樹定義:二叉樹每個子樹中,左樹最大高度和右樹最大高度差小於等於1。
1、遞歸套路思路
分析對於任意一個節點,滿足以此節點為頭的子樹是平衡二叉樹的條件(列出所有可能性)
(1)左樹是平衡二叉樹
(2)右樹是平衡二叉樹
(3)左樹高度、右樹高度 差值小於等於1
滿足這三個條件才能説以此節點為頭的子樹是平衡二叉樹。
也就是每次從左子樹和右子樹中我們都需要 是否平衡、高度 兩個數據,儘管我們最後只返回是否平衡,但是我們需要高度來輔助我們判斷是否平衡,所以可以定義如下的Info類
public static class Info{
public boolean isBalanced;
public int height;
public Info(boolean b, int h) {
this.isBalanced = b;
this.height = h;
}
}
2、遞歸套路代碼
(1)首先判斷為空時好不好設置,此時也是好設置的,節點為空時new Info(true, 0),即認為空節點是平衡二叉樹、高度為0。
(2)然後根據列出的所有可能性,編寫遞歸套路的代碼,因為要整個形成遞歸,所以每一步都要返回Info類。(拿到左右子樹的Info、拼湊自己的Info、返回自己的Info)
/**
* 判斷以某個節點為頭的子樹是否是平衡二叉樹
*
* @author Java和算法學習:週一
*/
public static Info process(Node x) {
if (x == null) {
return new Info(true, 0);
}
// 1.拿到左右子樹的信息
Info leftInfo = process(x.left);
Info rightInfo = process(x.right);
// 2.拼湊我自己的信息
// 默認是平衡的
boolean isBalanced = true;
// 哪些情況會造成不平衡:1.左樹不平衡 2.右樹不平衡 3.左右子樹的高度差大於1
if (!leftInfo.isBalanced || !rightInfo.isBalanced || Math.abs(leftInfo.height - rightInfo.height) > 1) {
isBalanced = false;
}
// 左右子樹中最大高度,加上到自己的高度
int height = Math.max(leftInfo.height, rightInfo.height) + 1;
// 3.返回自己的信息
return new Info(isBalanced, height);
}
(3)主函數調用遞歸方法獲取結果
/**
* @author Java和算法學習:週一
*/
public static boolean isBalancedBinaryTree(Node head) {
if (head == null) {
return true;
}
return process(head).isBalanced;
}
所有代碼地址:
https://github.com/monday-pro...
是不是發現用遞歸套路來解瞬間難度降低了許多,別急,二叉樹的遞歸套路遠不止這點,這才套路入門呢,後面還有好幾篇介紹遞歸套路技巧的。