2025-11-30：樹中找到帶權中位節點。用go語言，給出一個含 n 個節點（編號 0 到 n-1）的帶權無向樹，樹的根定為節點 0。樹用長度為 n-1 的數組 edges 描述，每個 edges[ 詳情 - include,數組,bc,Go語言,後端開發福大大架構師每日一題博客

2025-11-30：樹中找到帶權中位節點。用go語言，給出一個含 n 個節點（編號 0 到 n-1）的帶權無向樹，樹的根定為節點 0。樹用長度為 n-1 的數組 edges 描述，每個 edges[i] = [ui, vi, wi] 表示 ui 與 vi 之間有一條權值為 wi 的邊。

在兩節點間的路徑上，把從起點累積經過的邊權和視作距離。所謂“帶權中位節點”是指沿從起點 ui 到終點 vi 的路徑，從 ui 出發第一個使得累計邊權達到（或超過）整條路徑總權重一半的節點 x。

現在給出若干查詢 queries，每個 queries[j] = [uj, vj] 要求找出 uj 到 vj 路徑上的帶權中位節點。輸出一個數組 ans，其中 ans[j] 是對應查詢的帶權中位節點編號。

2 <= n <= 100000。

edges.length == n - 1。

edges[i] == [ui, vi, wi]。

0 <= ui, vi < n。

1 <= wi <= 1000000000。

1 <= queries.length <= 100000。

queries[j] == [uj, vj]。

0 <= uj, vj < n。

輸入保證 edges 表示一棵合法的樹。

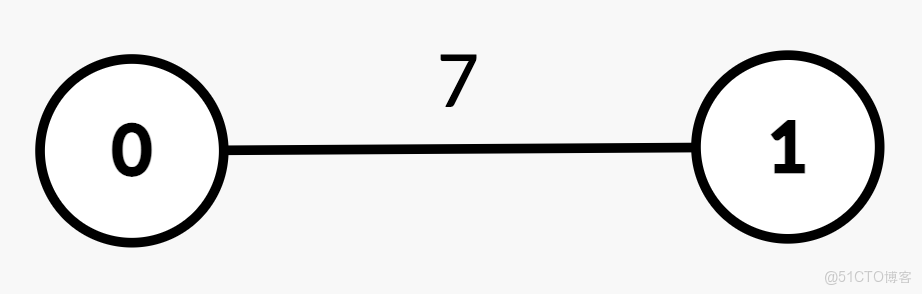
輸入： n = 2, edges = [[0,1,7]], queries = [[1,0],[0,1]]。

輸出： [0,1]。

解釋：

在這裏插入圖片描述

查詢	路徑	邊權	總路徑權值和	一半	解釋	答案
[1, 0]	1 → 0	[7]	7	3.5	從 1 → 0 的權重和為 7 ≥ 3.5，中位節點是 0。
[0, 1]	0 → 1	[7]	7	3.5	從 0 → 1 的權重和為 7 ≥ 3.5，中位節點是 1。	1

題目來自力扣3585。

步驟概述

圖的構建：將邊列表轉換為鄰接表表示的樹結構。
LCA預處理：通過DFS計算節點深度和距離，並構建倍增表以支持快速祖先查詢。
查詢處理：對每個查詢，計算路徑總權值、確定中位點位置，並利用倍增跳躍定位節點。
時間複雜度：預處理階段O(n log n)，查詢階段O(q log n)，總複雜度O((n + q) log n)。
空間複雜度：主要開銷來自存儲樹結構和倍增表，為O(n log n)。

詳細分步過程

步驟1: 構建樹結構（鄰接表）

輸入：邊列表edges，每條邊包含兩個節點和邊權值。
過程：
- 初始化一個大小為n的鄰接表g，每個節點對應一個列表，存儲相鄰節點及邊權。
- 遍歷所有邊，由於樹是無向的，每條邊在鄰接表中雙向添加（例如，邊(u, v, w)會同時添加到g[u]和g[v]的列表中）。
目的：為後續DFS遍歷提供高效的鄰接關係查詢。

步驟2: LCA預處理（DFS和倍增表構建）

**DFS遍歷（計算深度和距離）**：
- 從根節點0開始遞歸遍歷樹。
- 維護三個數組：
  - dep[]：記錄每個節點到根節點的深度（根節點深度為0）。
  - dis[]：記錄每個節點到根節點的路徑權值累加和（根節點距離為0）。
  - pa[][]：倍增表，pa[x][i]表示節點x的2^i級祖先節點。
- 對於當前節點x，遍歷其所有鄰居節點y（跳過父節點避免循環）。更新y的深度dep[y] = dep[x] + 1，距離dis[y] = dis[x] + 邊權。同時記錄y的直接父節點pa[y][0] = x。
構建倍增表：
- 計算最大跳躍層級mx = ceil(log₂(n))（例如n=100,000時，mx≈17）。
- 通過動態規劃填充pa數組：對於每個層級i（從1到mx-1），遍歷所有節點x，若pa[x][i-1]存在，則pa[x][i] = pa[pa[x][i-1]][i-1]（即x的2^i祖先等於x的2^{i-1}祖先的2^{i-1}祖先）。
目的：將任意兩點路徑查詢轉化為O(log n)時間的跳躍操作。

步驟3: 處理查詢（定位帶權中位節點）

對每個查詢queries[j] = [u, v]，執行以下子步驟：

特判相同節點：若u == v，直接返回u作為中位節點（路徑權值為0，節點自身即中點）。
計算LCA和路徑總權值：
- 調用getLCA(u, v)找到最近公共祖先lca（算法：先將u和v調整到同一深度，然後同步向上跳躍直至相遇）。
- 路徑總權值dist = dis[u] + dis[v] - 2*dis[lca]（利用到根節點距離的差值計算）。
- 計算半權值閾值half = (dist + 1) / 2（向上取整，確保累計權值≥一半）。
確定中位節點位置：
- 判斷u到lca的子路徑權值是否足夠覆蓋half：
  - 若dis[u] - dis[lca] ≥ half：
    - 中位節點位於u到lca的路徑上。
    - 從u向上回溯至多half-1權值（通過uptoDis函數）：沿倍增表從高位到低位嘗試跳躍，確保跳躍後累計距離不超過half-1。
    - 此時到達節點to，中位節點是to的父節點pa[to][0]（再跳一步即超過half）。
  - 否則中位節點位於v到lca的路徑上：
    - 從v向上回溯權值dist - half（即從v出發走剩餘路徑達到half）。
    - 直接調用uptoDis(v, dist - half)定位節點，該節點即為中位節點。
輸出結果：將每個查詢的結果存入答案數組ans。

示例驗證（針對輸入n=2, edges=[[0,1,7]], queries=[[1,0],[0,1]]）

**查詢[1,0]**：
- LCA為0，路徑總權值=7，half=4。
- dis[1]-dis[0]=7≥4，中位在1→0路徑。從1回溯min(4-1,7)=3權值（實際回溯0權值，因半路已超），跳至父節點0，輸出0。
**查詢[0,1]**：
- 路徑相同，half=4。dis[0]-dis[0]=0<4，中位在1→0路徑。從1回溯7-4=3權值（實際回溯至1本身），輸出1。

時間複雜度和空間複雜度

時間複雜度：
- 預處理：DFS遍歷O(n)，倍增表構建O(n log n)。
- 每個查詢：LCA計算O(log n)，路徑權值計算O(1)，跳躍操作O(log n)。
- 總時間：O(n log n + q log n)，適用於n, q ≤ 100,000。
空間複雜度：
- 鄰接表O(n)，倍增表O(n log n)，dep/dis數組O(n)。
- 總空間：O(n log n)。

Go完整代碼如下：

package main

import (
	"fmt"
	"math/bits"
)

func findMedian(n int, edges [][]int, queries [][]int) []int {
	type edge struct{ to, wt int }
	g := make([][]edge, n)
	for _, e := range edges {
		x, y, wt := e[0], e[1], e[2]
		g[x] = append(g[x], edge{y, wt})
		g[y] = append(g[y], edge{x, wt})
	}

	// 17 可以替換成 bits.Len(uint(n))，但數組內存連續性更好
	pa := make([][17]int, n)
	dep := make([]int, n)
	dis := make([]int, n)

	var dfs func(int, int)
	dfs = func(x, p int) {
		pa[x][0] = p
		for _, e := range g[x] {
			y := e.to
			if y == p {
				continue
			}
			dep[y] = dep[x] + 1
			dis[y] = dis[x] + e.wt
			dfs(y, x)
		}
	}
	dfs(0, -1)

	mx := bits.Len(uint(n))
	for i := range mx - 1 {
		for x := range pa {
			p := pa[x][i]
			if p != -1 {
				pa[x][i+1] = pa[p][i]
			} else {
				pa[x][i+1] = -1
			}
		}
	}

	uptoDep := func(x, d int) int {
		for k := uint(dep[x] - d); k > 0; k &= k - 1 {
			x = pa[x][bits.TrailingZeros(k)]
		}
		return x
	}

	// 返回 x 和 y 的最近公共祖先（節點編號從 0 開始）
	getLCA := func(x, y int) int {
		if dep[x] > dep[y] {
			x, y = y, x
		}
		y = uptoDep(y, dep[x]) // 使 y 和 x 在同一深度
		if y == x {
			return x
		}
		for i := mx - 1; i >= 0; i-- {
			px, py := pa[x][i], pa[y][i]
			if px != py {
				x, y = px, py // 同時往上跳 2^i 步
			}
		}
		return pa[x][0]
	}

	// 從 x 往上跳【至多】d 距離，返回最遠能到達的節點
	uptoDis := func(x, d int) int {
		dx := dis[x]
		for i := mx - 1; i >= 0; i-- {
			p := pa[x][i]
			if p != -1 && dx-dis[p] <= d { // 可以跳至多 d
				x = p
			}
		}
		return x
	}

	// 以上是 LCA 模板

	ans := make([]int, len(queries))
	for i, q := range queries {
		x, y := q[0], q[1]
		if x == y {
			ans[i] = x
			continue
		}
		lca := getLCA(x, y)
		disXY := dis[x] + dis[y] - dis[lca]*2
		half := (disXY + 1) / 2
		if dis[x]-dis[lca] >= half { // 答案在 x-lca 路徑中
			// 先往上跳至多 half-1，然後再跳一步，就是至少 half
			to := uptoDis(x, half-1)
			ans[i] = pa[to][0] // 再跳一步
		} else { // 答案在 y-lca 路徑中
			// 從 y 出發至多 disXY-half，就是從 x 出發至少 half
			ans[i] = uptoDis(y, disXY-half)
		}
	}
	return ans
}

func main() {
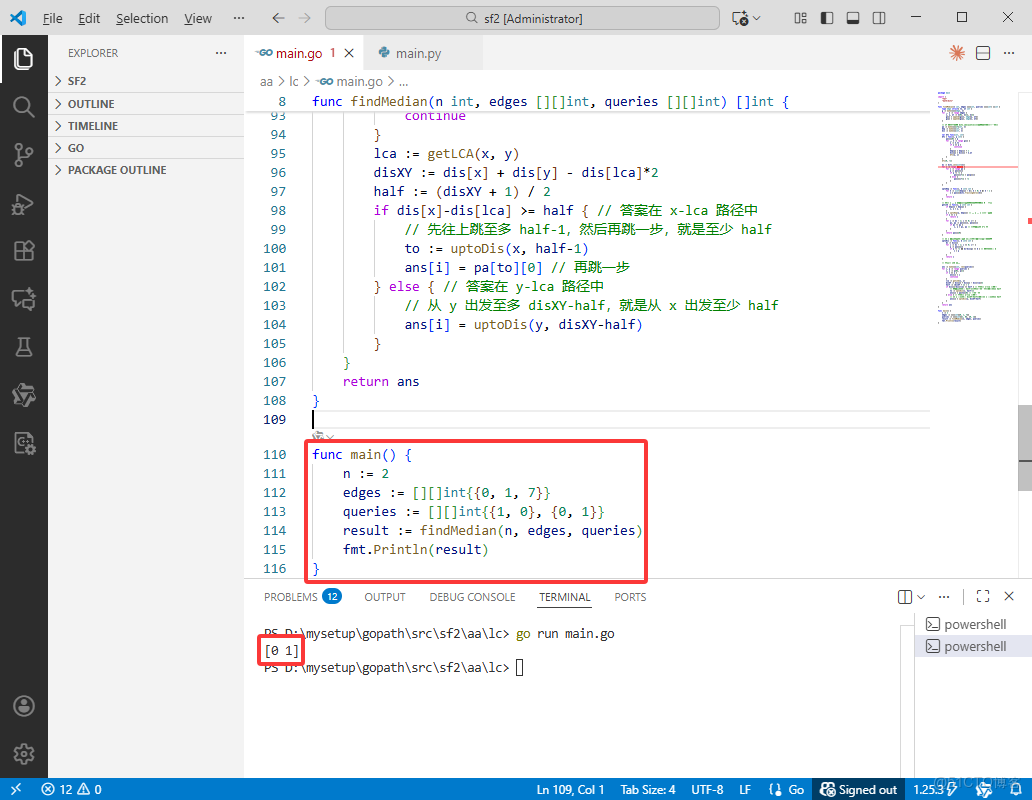
	n := 2
	edges := [][]int{{0, 1, 7}}
	queries := [][]int{{1, 0}, {0, 1}}
	result := findMedian(n, edges, queries)
	fmt.Println(result)
}

在這裏插入圖片描述

Python完整代碼如下：

# -*-coding:utf-8-*-

import math
from typing import List

def findMedian(n: int, edges: List[List[int]], queries: List[List[int]]) -> List[int]:
    # 構建圖的鄰接表
    graph = [[] for _ in range(n)]
    for e in edges:
        x, y, wt = e
        graph[x].append((y, wt))
        graph[y].append((x, wt))
    
    # 計算倍增數組的深度
    mx = n.bit_length()
    
    # 初始化數組
    parent = [[-1] * mx for _ in range(n)]
    depth = [0] * n
    distance = [0] * n
    
    # DFS預處理
    def dfs(x: int, p: int):
        parent[x][0] = p
        for y, wt in graph[x]:
            if y == p:
                continue
            depth[y] = depth[x] + 1
            distance[y] = distance[x] + wt
            dfs(y, x)
    
    dfs(0, -1)
    
    # 構建倍增數組
    for i in range(mx - 1):
        for x in range(n):
            p = parent[x][i]
            if p != -1:
                parent[x][i + 1] = parent[p][i]
            else:
                parent[x][i + 1] = -1
    
    # 將節點x提升到深度d
    def upto_depth(x: int, d: int) -> int:
        k = depth[x] - d
        while k > 0:
            step = k & -k  # 獲取最低位的1
            x = parent[x][step.bit_length() - 1]
            k -= step
        return x
    
    # 獲取最近公共祖先
    def get_lca(x: int, y: int) -> int:
        if depth[x] > depth[y]:
            x, y = y, x
        y = upto_depth(y, depth[x])
        if y == x:
            return x
        
        for i in range(mx - 1, -1, -1):
            px, py = parent[x][i], parent[y][i]
            if px != py:
                x, y = px, py
        return parent[x][0]
    
    # 從x向上跳至多d距離
    def upto_distance(x: int, d: int) -> int:
        dx = distance[x]
        for i in range(mx - 1, -1, -1):
            p = parent[x][i]
            if p != -1 and dx - distance[p] <= d:
                x = p
        return x
    
    # 處理查詢
    result = []
    for q in queries:
        x, y = q
        if x == y:
            result.append(x)
            continue
            
        lca = get_lca(x, y)
        dis_xy = distance[x] + distance[y] - 2 * distance[lca]
        half = (dis_xy + 1) // 2
        
        if distance[x] - distance[lca] >= half:
            # 答案在x到lca的路徑上
            to = upto_distance(x, half - 1)
            result.append(parent[to][0])
        else:
            # 答案在y到lca的路徑上
            result.append(upto_distance(y, dis_xy - half))
    
    return result

# 測試代碼
if __name__ == "__main__":
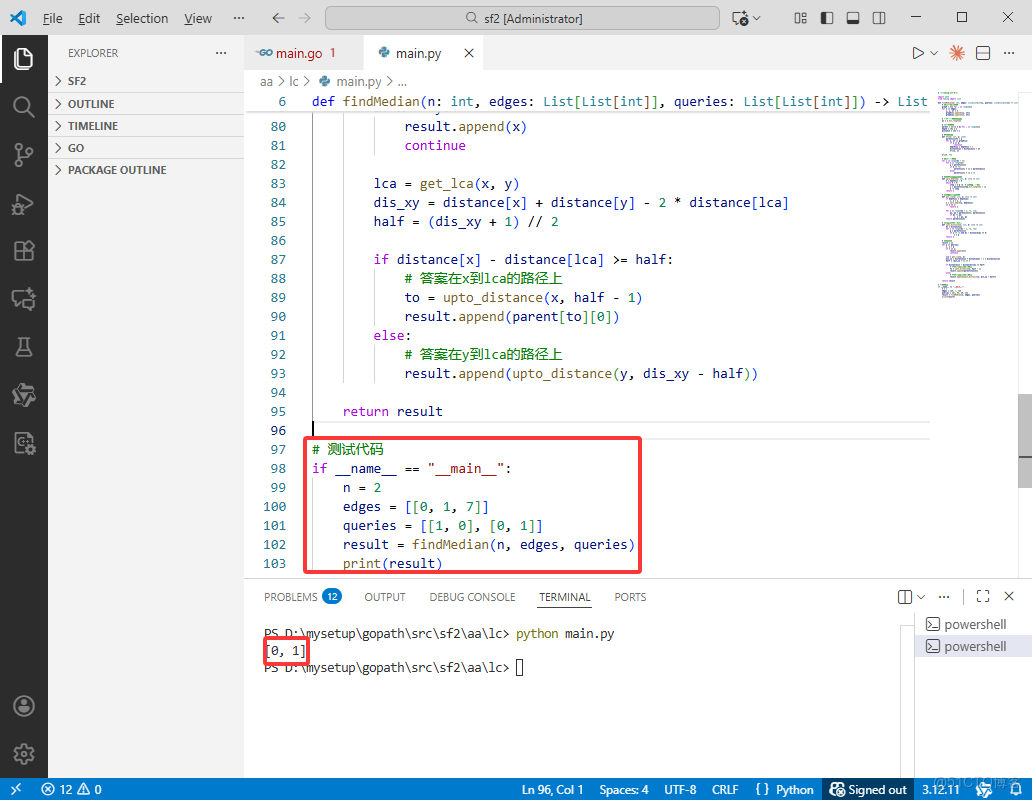
    n = 2
    edges = [[0, 1, 7]]
    queries = [[1, 0], [0, 1]]
    result = findMedian(n, edges, queries)
    print(result)

在這裏插入圖片描述

C++完整代碼如下：

#include <iostream>
#include <vector>
#include <cmath>
#include <cstring>
using namespace std;

struct Edge {
    int to, wt;
};

class TreeMedianFinder {
public:
    int n, mx;
    vector<vector<Edge>> g;
    vector<vector<int>> pa; // pa[x][i]：x 的 2^i 級祖先
    vector<int> dep, dis;

    TreeMedianFinder(int n, const vector<vector<int>>& edges) : n(n) {
        g.assign(n, {});
        for (auto& e : edges) {
            int x = e[0], y = e[1], wt = e[2];
            g[x].push_back({y, wt});
            g[y].push_back({x, wt});
        }
        mx = 32 - __builtin_clz(n); // bits.Len(n)
        pa.assign(n, vector<int>(mx, -1));
        dep.assign(n, 0);
        dis.assign(n, 0);

        dfs(0, -1);

        // 倍增預處理
        for (int i = 0; i < mx - 1; i++) {
            for (int x = 0; x < n; x++) {
                if (pa[x][i] != -1)
                    pa[x][i + 1] = pa[pa[x][i]][i];
                else
                    pa[x][i + 1] = -1;
            }
        }
    }

    void dfs(int x, int p) {
        pa[x][0] = p;
        for (auto& e : g[x]) {
            int y = e.to;
            if (y == p) continue;
            dep[y] = dep[x] + 1;
            dis[y] = dis[x] + e.wt;
            dfs(y, x);
        }
    }

    // 跳到指定深度
    int uptoDep(int x, int d) {
        int diff = dep[x] - d;
        while (diff > 0) {
            int k = __builtin_ctz(diff); // 低位 1 的位置
            x = pa[x][k];
            diff &= diff - 1;
        }
        return x;
    }

    // 最近公共祖先
    int getLCA(int x, int y) {
        if (dep[x] > dep[y]) swap(x, y);
        y = uptoDep(y, dep[x]);
        if (x == y) return x;
        for (int i = mx - 1; i >= 0; i--) {
            if (pa[x][i] != pa[y][i]) {
                x = pa[x][i];
                y = pa[y][i];
            }
        }
        return pa[x][0];
    }

    // 從 x 往上跳至多 d 距離
    int uptoDis(int x, int d) {
        int dx = dis[x];
        for (int i = mx - 1; i >= 0; i--) {
            int p = pa[x][i];
            if (p != -1 && dx - dis[p] <= d) {
                x = p;
            }
        }
        return x;
    }

    vector<int> solveQueries(const vector<vector<int>>& queries) {
        vector<int> ans;
        ans.reserve(queries.size());
        for (auto& q : queries) {
            int x = q[0], y = q[1];
            if (x == y) {
                ans.push_back(x);
                continue;
            }
            int lca = getLCA(x, y);
            int disXY = dis[x] + dis[y] - 2 * dis[lca];
            int half = (disXY + 1) / 2;
            if (dis[x] - dis[lca] >= half) {
                // 在 x-lca 路徑中
                int to = uptoDis(x, half - 1);
                ans.push_back(pa[to][0]);
            } else {
                // 在 y-lca 路徑中
                ans.push_back(uptoDis(y, disXY - half));
            }
        }
        return ans;
    }
};

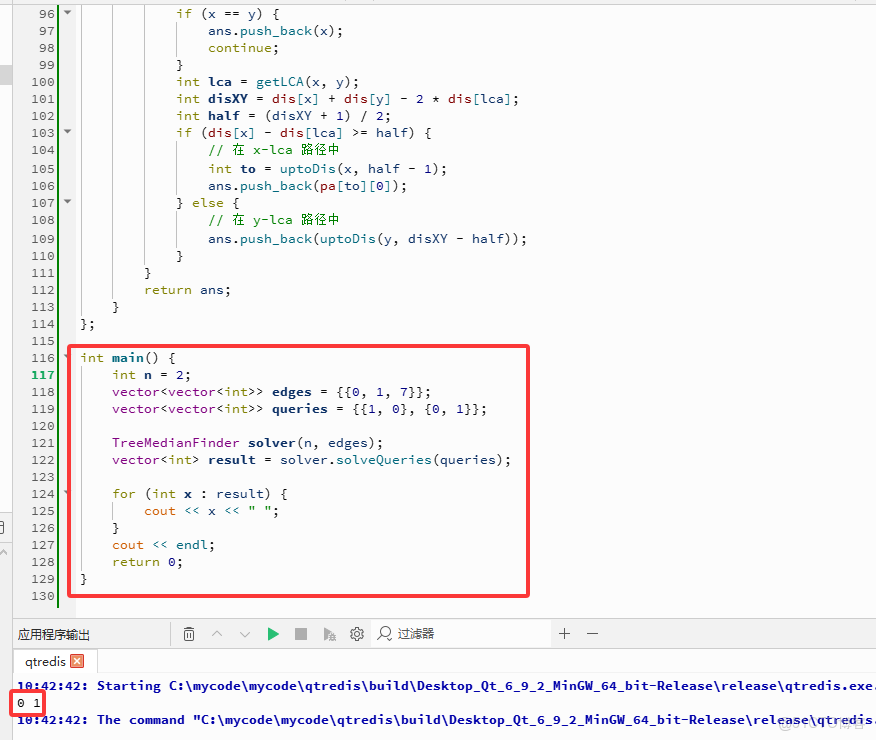
int main() {
    int n = 2;
    vector<vector<int>> edges = {{0, 1, 7}};
    vector<vector<int>> queries = {{1, 0}, {0, 1}};

    TreeMedianFinder solver(n, edges);
    vector<int> result = solver.solveQueries(queries);

    for (int x : result) {
        cout << x << " ";
    }
    cout << endl;
    return 0;
}

在這裏插入圖片描述

福大大架構師每日一題博客

福大大架構師每日一題博客

博客 / 詳情