2025-11-25:統計極差最大為 K 的分割方式數。用go語言,給定一個整數數組 nums 和一個整數 k。
要求把 nums 劃分成若干個相鄰且非空的子數組(分段),使得每一段內元素的最大值與最小值之差不超過 k。
求符合條件的所有劃分方案的數量。結果可能很大,請對 1000000007 取模後輸出。
2 <= nums.length <= 50000。
1 <= nums[i] <= 1000000000。
0 <= k <= 1000000000。
輸入: nums = [9,4,1,3,7], k = 4。
輸出: 6。
解釋:
共有 6 種有效的分割方式,使得每個子段中的最大值與最小值之差不超過 k = 4:
[[9], [4], [1], [3], [7]]
[[9], [4], [1], [3, 7]]
[[9], [4], [1, 3], [7]]
[[9], [4, 1], [3], [7]]
[[9], [4, 1], [3, 7]]
[[9], [4, 1, 3], [7]]
題目來自力扣3578。
📝 程序運行步驟分解
-
初始化
- 創建一個DP數組
f,其中f[i]表示數組前i個元素(即nums[0]到nums[i-1])的有效分割方案數量。初始時,f[0]被設置為1,這表示一個空數組有一種分割方式(即不進行任何分割的基礎情況)。 - 初始化兩個空的單調隊列
minQ和maxQ,分別用於維護當前窗口內的最小值和最大值的索引。這兩個隊列是保證高效計算極差的關鍵。 - 變量
sumF用於記錄當前滑動窗口內有效的DP值之和。變量left作為滑動窗口的左邊界指針,初始為0。
- 創建一個DP數組
-
遍歷數組並處理每個元素 程序從左到右遍歷數組,對於每個當前位置
i(對應元素x = nums[i]),執行以下三個主要操作:-
A. 元素入隊並維護單調隊列
- 將
f[i]的值加到sumF中。這相當於為後續計算積累以i-1位置結尾的分割方案數。 - 將當前索引
i加入到單調隊列中,並維護隊列的單調性:minQ(遞增隊列):從隊尾開始,移除所有其對應元素值大於或等於當前元素x的索引。然後將i加入隊尾。這確保了隊頭始終是當前窗口內最小值的索引。maxQ(遞減隊列):從隊尾開始,移除所有其對應元素值小於或等於當前元素x的索引。然後將i加入隊尾。這確保了隊頭始終是當前窗口內最大值的索引。
- 這個過程保證了隊列是單調的,且隊首元素就是當前窗口的極值。
- 將
-
B. 調整窗口左邊界(出隊)
- 計算當前窗口
[left, i]的極差,即nums[maxQ[0]] - nums[minQ[0]]。 - 如果該極差大於給定的
k,則意味着當前窗口不符合條件。需要不斷將左邊界left向右移動,以縮小窗口範圍,直到極差小於等於k。- 在移動
left時,從sumF中減去f[left],因為以left為結尾的分割方案不再適用於新的窗口。 - 同時,檢查兩個單調隊列的隊首索引是否已經小於新的
left。如果是,則將該隊首出隊,因為它已經不在當前窗口內了。
- 在移動
- 此步驟確保了窗口
[left, i]是滿足極差條件的、以i為右端點的最長子數組。
- 計算當前窗口
-
C. 更新動態規劃數組
- 在確保了窗口
[left, i]的有效性後,當前的sumF就代表了所有能夠有效分割到當前位置i的方案總數。 - 因此,將
f[i+1]更新為sumF % mod。這表示,所有能夠有效分割到i的方案,都可以通過在其末尾添加一個以i結尾的合法子段來形成一種新的分割方案。
- 在確保了窗口
-
-
返回結果
- 當遍歷完整個數組後,DP數組
f的最後一個元素f[n]就是整個數組nums的有效分割方案總數,將其返回即可。
- 當遍歷完整個數組後,DP數組
⏱️ 複雜度分析
-
總的時間複雜度:O(n)。 整個算法只對數組進行了一次遍歷。雖然內部有循環,但每個元素最多被壓入和彈出單調隊列各一次,因此所有操作的平均時間複雜度是常數級別的。所以,總時間複雜度是線性的 O(n)。
-
總的額外空間複雜度:O(n)。 主要的空間開銷來自於DP數組
f(大小為 n+1)以及兩個單調隊列minQ和maxQ(最壞情況下各需要 O(n) 空間)。因此,總的空間複雜度是 O(n)。
Go完整代碼如下:
package main
import (
"fmt"
)
func countPartitions(nums []int, k int) int {
const mod = 1_000_000_007
n := len(nums)
var minQ, maxQ []int
f := make([]int, n+1)
f[0] = 1
sumF := 0 // 窗口中的 f[i] 之和
left := 0
for i, x := range nums {
// 1. 入
sumF += f[i]
for len(minQ) > 0 && x <= nums[minQ[len(minQ)-1]] {
minQ = minQ[:len(minQ)-1]
}
minQ = append(minQ, i)
for len(maxQ) > 0 && x >= nums[maxQ[len(maxQ)-1]] {
maxQ = maxQ[:len(maxQ)-1]
}
maxQ = append(maxQ, i)
// 2. 出
for nums[maxQ[0]]-nums[minQ[0]] > k {
sumF -= f[left]
left++
if minQ[0] < left {
minQ = minQ[1:]
}
if maxQ[0] < left {
maxQ = maxQ[1:]
}
}
// 3. 更新答案
f[i+1] = sumF % mod
}
return f[n]
}
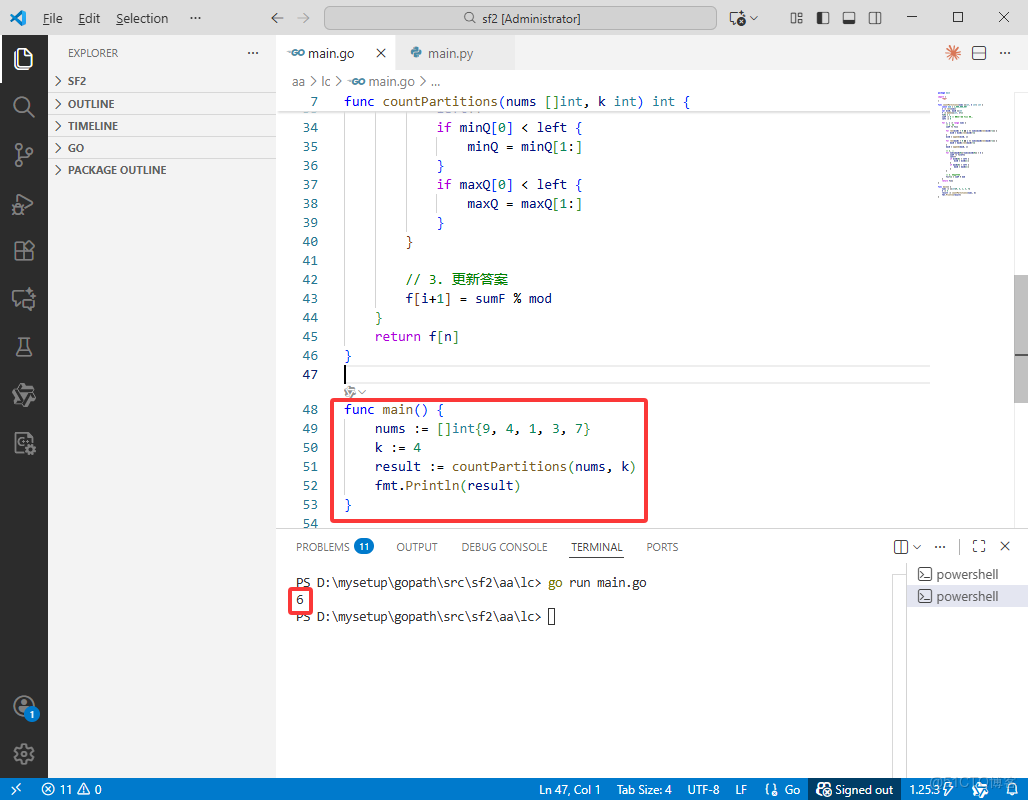
func main() {
nums := []int{9, 4, 1, 3, 7}
k := 4
result := countPartitions(nums, k)
fmt.Println(result)
}
Python完整代碼如下:
# -*-coding:utf-8-*-
from collections import deque
def countPartitions(nums, k):
mod = 1_000_000_007
n = len(nums)
min_q = deque()
max_q = deque()
f = [0] * (n + 1)
f[0] = 1
sum_f = 0 # 窗口中的 f[i] 之和
left = 0
for i, x in enumerate(nums):
# 1. 入
sum_f = (sum_f + f[i]) % mod
# 維護最小值的單調隊列
while min_q and x <= nums[min_q[-1]]:
min_q.pop()
min_q.append(i)
# 維護最大值的單調隊列
while max_q and x >= nums[max_q[-1]]:
max_q.pop()
max_q.append(i)
# 2. 出
while nums[max_q[0]] - nums[min_q[0]] > k:
sum_f = (sum_f - f[left]) % mod
left += 1
if min_q[0] < left:
min_q.popleft()
if max_q[0] < left:
max_q.popleft()
# 3. 更新答案
f[i + 1] = sum_f % mod
return f[n]
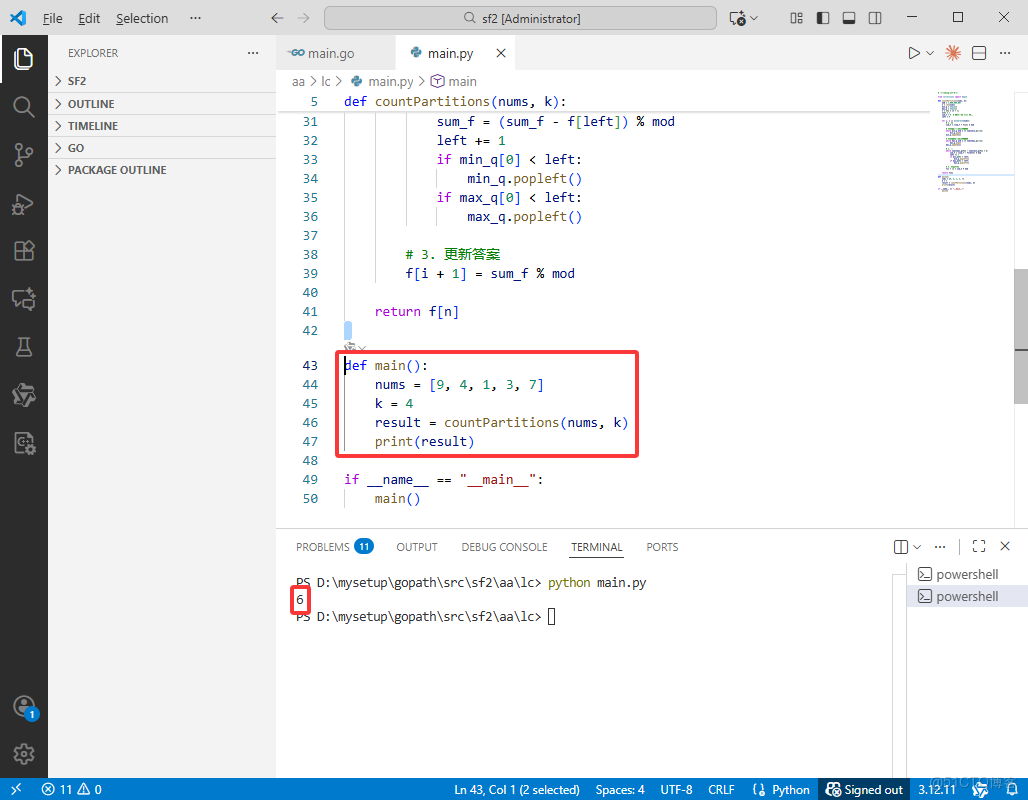
def main():
nums = [9, 4, 1, 3, 7]
k = 4
result = countPartitions(nums, k)
print(result)
if __name__ == "__main__":
main()
C++完整代碼如下:
#include <iostream>
#include <vector>
#include <deque>
using namespace std;
class Solution {
public:
int countPartitions(vector<int>& nums, int k) {
const int mod = 1'000'000'007;
int n = nums.size();
deque<int> minQ, maxQ;
vector<int> f(n + 1, 0);
f[0] = 1;
long long sumF = 0; // 窗口中的 f[i] 之和
int left = 0;
for (int i = 0; i < n; i++) {
int x = nums[i];
// 1. 入
sumF = (sumF + f[i]) % mod;
// 維護最小值的單調隊列
while (!minQ.empty() && x <= nums[minQ.back()]) {
minQ.pop_back();
}
minQ.push_back(i);
// 維護最大值的單調隊列
while (!maxQ.empty() && x >= nums[maxQ.back()]) {
maxQ.pop_back();
}
maxQ.push_back(i);
// 2. 出
while (nums[maxQ.front()] - nums[minQ.front()] > k) {
sumF = (sumF - f[left] + mod) % mod;
left++;
if (minQ.front() < left) {
minQ.pop_front();
}
if (maxQ.front() < left) {
maxQ.pop_front();
}
}
// 3. 更新答案
f[i + 1] = sumF % mod;
}
return f[n];
}
};
int main() {
vector<int> nums = {9, 4, 1, 3, 7};
int k = 4;
Solution solution;
int result = solution.countPartitions(nums, k);
cout << result << endl;
return 0;
}