2025-11-15：等積子集的劃分方案。用go語言，給定一個只包含不同正整數的數組 nums 和一個整數 target。要求把 nums 的所有元素分成兩組（每個元素只能屬於其中一組，且兩組都不能為空），使得每一組中所有數相乘的結果都等於 target。若存在這樣的分組返回 true，否則返回 false。

3 <= nums.length <= 12。

1 <= target <= 1000000000000000。

1 <= nums[i] <= 100。

nums 中的所有元素互不相同。

輸入： nums = [3,1,6,8,4], target = 24。

輸出： true。

解釋：子集 [3, 8] 和 [1, 6, 4] 的乘積均為 24。因此，輸出為 true 。

題目來自力扣3566。

分步驟詳細過程

  1. 整體乘積驗證

    • 首先，計算整個數組 nums 中所有元素的乘積。如果整個數組的乘積不等於 target 的平方（即 target * target），則直接返回 false。這是因為問題要求將數組劃分為兩個子集後，每個子集的乘積都等於 target，因此整個數組的乘積必須恰好為 target²。
    • 例如，在示例 nums = [3,1,6,8,4] 和 target = 24 中，整個數組的乘積為 3*1*6*8*4 = 576，而 24² = 576，因此通過驗證。

  2. 分治分割數組

    • 將數組 nums 近似分成兩半：前半部分為 nums[:m]，後半部分為 nums[m:]，其中 m 是 len(nums) / 2（例如，當 n=5 時，前半部分包含前2個或3個元素，具體取決於實現）。這種分治策略的目的是將指數級複雜度的枚舉問題分解為兩個規模減半的子問題。
    • 分治後，前半部分和後半部分分別獨立處理，減少需要枚舉的狀態數。

  3. 生成前半部分的乘積比例集合（使用DFS）

    • 對前半部分數組執行DFS，遞歸地枚舉每個元素被劃分到第一個子集（記為乘積 a）或第二個子集（記為乘積 b）的所有可能方式。DFS的起點為 a=1 和 b=1（乘法的單位元）。
    • 當處理完前半部分所有元素後，計算 a 和 b 的最簡分數比例：即計算 a 和 b 的最大公約數（GCD），然後將比例簡化為 (a/gcd, b/gcd)。這個比例表示兩個子集乘積的相對大小，而非具體值，從而避免數值溢出並簡化匹配。
    • 所有最簡比例被存儲在一個集合 set1 中（例如，使用Map結構，鍵為比例對）。如果DFS過程中 a 或 b 超過 target，則剪枝提前返回，因為後續乘法只會使乘積更大。

  4. 生成後半部分的乘積比例集合（同樣使用DFS）

    • 對後半部分數組執行相同的DFS過程：枚舉每個元素劃分到第一個子集（乘積記為 c）或第二個子集（乘積記為 d）的所有情況。
    • 處理完後半部分後，同樣計算 c 和 d 的最簡比例 (c/gcd, d/gcd)，並存儲在另一個集合 set2 中。

  5. 合併檢查比例匹配

    • 檢查 set1 和 set2 中是否存在相同的比例對。如果存在這樣的比例，則表明可以將前半部分和後半部分的劃分組合成一個有效解：
      • 具體來説，如果前半部分的比例為 (p, q)，後半部分的比例為 (q, p)，則組合後整個數組的第一個子集乘積為 p * q = target，第二個子集乘積為 q * p = target（因為整個數組乘積為 target²）。
    • 例如，示例中前半部分可能生成比例 (3, 1)（對應子集乘積為3和1），後半部分生成比例 (8, 2)，但需注意實際匹配時比例需互補。代碼中通過集合查找直接驗證是否存在公共比例。
    • 如果找到匹配，返回 true；否則返回 false。

總時間複雜度和總額外空間複雜度

  • 時間複雜度：

    • 整個過程的核心是DFS枚舉。數組長度 n 最大為12，分治後每半部分長度約為 n/2（即最多6）。DFS枚舉每半部分的所有劃分方式，每個元素有2種選擇（分配給第一個或第二個子集），因此每半部分的DFS狀態數為 O(2^{n/2})。
    • 計算GCD的時間可視為常數（因為數字乘積受 target ≤ 10^15 和 nums[i] ≤ 100 限制，數值範圍有限）。
    • 總時間複雜度為 O(2^{n/2})，分治策略將指數基數減半，優於直接枚舉的 O(2^n)。

  • 總額外空間複雜度：

    • 主要空間開銷用於存儲兩個比例集合 set1 和 set2。每個集合最多包含 O(2^{n/2}) 個比例對（每個比例對是兩個整數）。
    • DFS遞歸棧的深度為 O(n)，空間可忽略。
    • 因此，總額外空間複雜度為 O(2^{n/2})。

該方法通過分治和比例匹配巧妙降低了計算複雜度，適用於題目中的小規模約束（n ≤ 12）。

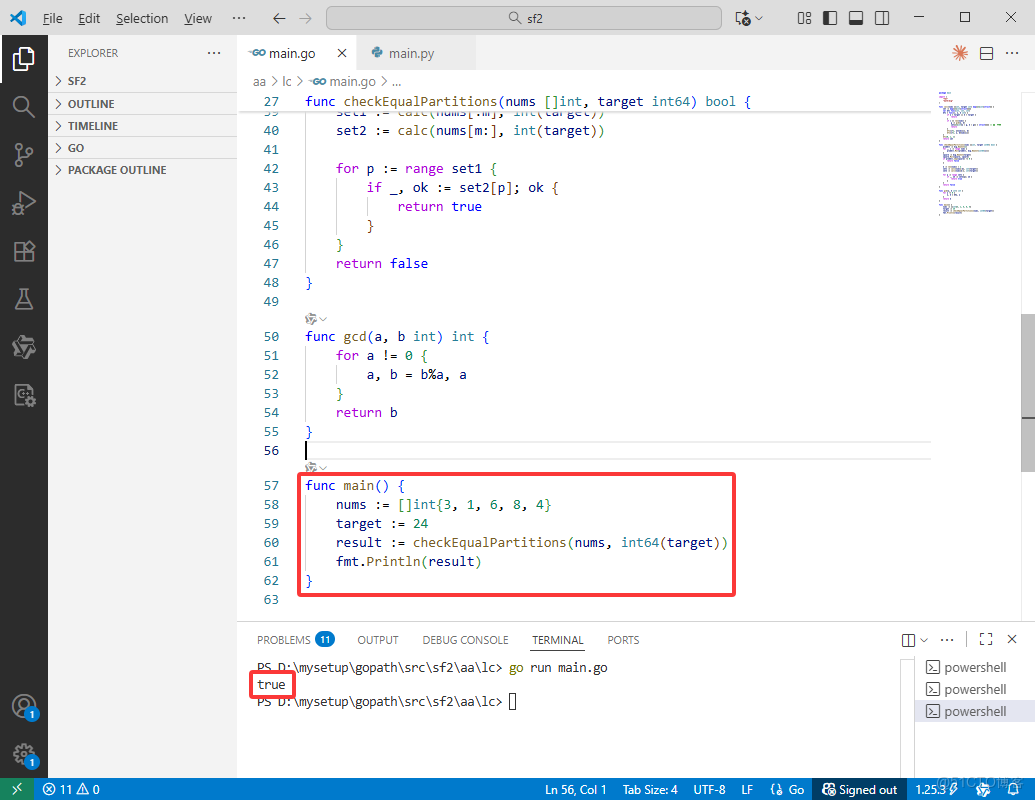
Go完整代碼如下：

package main

import (
	"fmt"
	"math/big"
)

func calc(nums []int, target int) map[[2]int]struct{} {
	set := map[[2]int]struct{}{}
	var dfs func(int, int, int)
	dfs = func(i, a, b int) {
		if a > target || b > target {
			return
		}
		if i == len(nums) {
			g := gcd(a, b)
			set[[2]int{a / g, b / g}] = struct{}{} // 最簡分數
			return
		}
		dfs(i+1, a*nums[i], b)
		dfs(i+1, a, b*nums[i])
	}
	dfs(0, 1, 1)
	return set
}

func checkEqualPartitions(nums []int, target int64) bool {
	prodAll := big.NewInt(1)
	for _, x := range nums {
		prodAll.Mul(prodAll, big.NewInt(int64(x)))
	}
	square := big.NewInt(target)
	square.Mul(square, square)
	if prodAll.Cmp(square) != 0 {
		return false
	}

	m := len(nums) / 2
	set1 := calc(nums[:m], int(target))
	set2 := calc(nums[m:], int(target))

	for p := range set1 {
		if _, ok := set2[p]; ok {
			return true
		}
	}
	return false
}

func gcd(a, b int) int {
	for a != 0 {
		a, b = b%a, a
	}
	return b
}

func main() {
	nums := []int{3, 1, 6, 8, 4}
	target := 24
	result := checkEqualPartitions(nums, int64(target))
	fmt.Println(result)
}

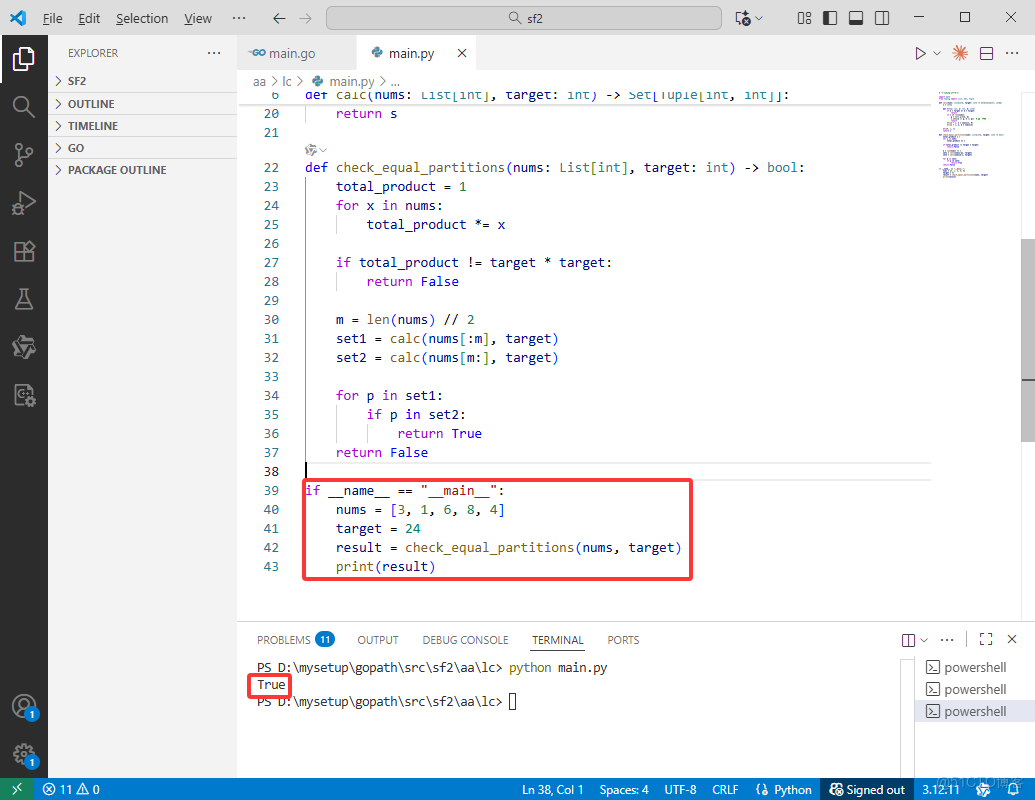
在這裏插入圖片描述

Python完整代碼如下：

# -*-coding:utf-8-*-

import math
from typing import List, Set, Tuple

def calc(nums: List[int], target: int) -> Set[Tuple[int, int]]:
    s = set()
    
    def dfs(i: int, a: int, b: int):
        if a > target or b > target:
            return
        if i == len(nums):
            g = math.gcd(a, b)
            s.add((a // g, b // g))  # 最簡分數
            return
        dfs(i + 1, a * nums[i], b)
        dfs(i + 1, a, b * nums[i])
    
    dfs(0, 1, 1)
    return s

def check_equal_partitions(nums: List[int], target: int) -> bool:
    total_product = 1
    for x in nums:
        total_product *= x
    
    if total_product != target * target:
        return False
    
    m = len(nums) // 2
    set1 = calc(nums[:m], target)
    set2 = calc(nums[m:], target)
    
    for p in set1:
        if p in set2:
            return True
    return False

if __name__ == "__main__":
    nums = [3, 1, 6, 8, 4]
    target = 24
    result = check_equal_partitions(nums, target)
    print(result)

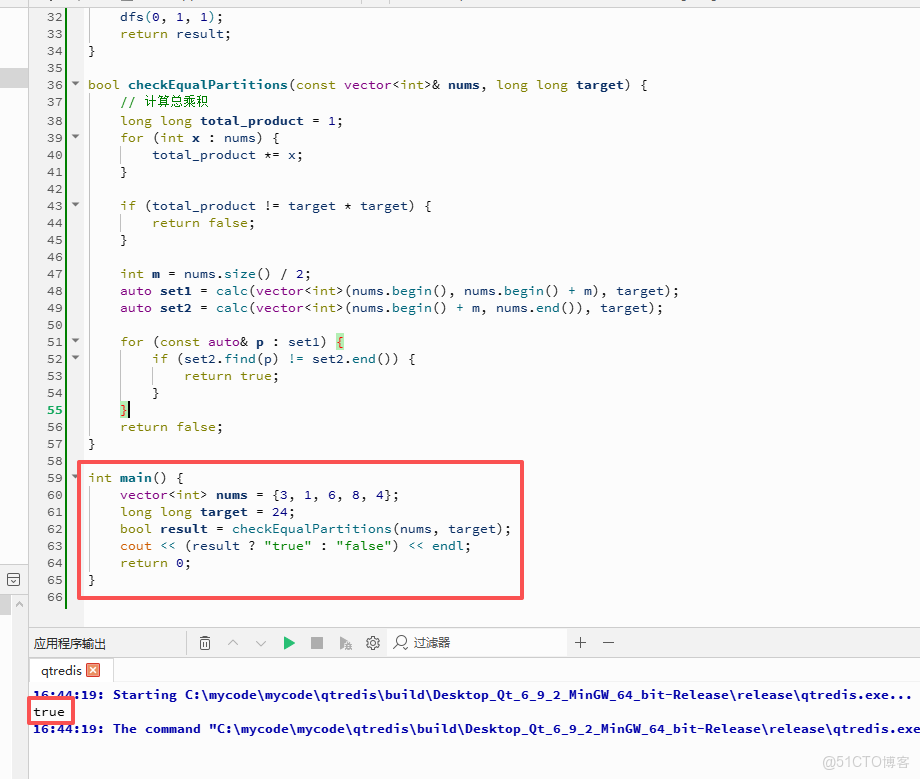
在這裏插入圖片描述

C++完整代碼如下：

#include <iostream>
#include <vector>
#include <set>
#include <functional>
#include <numeric>

using namespace std;

int gcd(int a, int b) {
    while (a != 0) {
        int temp = a;
        a = b % a;
        b = temp;
    }
    return b;
}

set<pair<int, int>> calc(const vector<int>& nums, int target) {
    set<pair<int, int>> result;

    function<void(int, int, int)> dfs = [&](int i, int a, int b) {
        if (a > target || b > target) return;
        if (i == nums.size()) {
            int g = gcd(a, b);
            result.insert({a / g, b / g}); // 最簡分數
            return;
        }
        dfs(i + 1, a * nums[i], b);
        dfs(i + 1, a, b * nums[i]);
    };

    dfs(0, 1, 1);
    return result;
}

bool checkEqualPartitions(const vector<int>& nums, long long target) {
    // 計算總乘積
    long long total_product = 1;
    for (int x : nums) {
        total_product *= x;
    }

    if (total_product != target * target) {
        return false;
    }

    int m = nums.size() / 2;
    auto set1 = calc(vector<int>(nums.begin(), nums.begin() + m), target);
    auto set2 = calc(vector<int>(nums.begin() + m, nums.end()), target);

    for (const auto& p : set1) {
        if (set2.find(p) != set2.end()) {
            return true;
        }
    }
    return false;
}

int main() {
    vector<int> nums = {3, 1, 6, 8, 4};
    long long target = 24;
    bool result = checkEqualPartitions(nums, target);
    cout << (result ? "true" : "false") << endl;
    return 0;
}

在這裏插入圖片描述