背景
密態計算能夠支持多方聯合建模而不泄漏數據價值。該方案是基於螞蟻密算隱語團隊開發的 Secret Sharing - Generalized Linear Model (SS-GLM) 算法完成了聯合建模的步驟。
很多業務小夥伴們多次詢問我們是否可以進一步提升該算法的性能。
通過分析 SS-GLM 算法的性能,我們發現 exp 算子佔用了40%以上的計算時間,高於其他任何單一操作。
根據德摩根定律,如果能夠改進 exp 算子,將會帶來最大的性能提升。此外,exp 算子廣泛應用於機器學習模型中的激活函數,甚至在大型模型如 Transformer 中也有大量的 exp 計算。
過去的方法往往犧牲精度,或者為特定模型提供特定的啓發式算子來提高性能。雖然這些方法在少數場景中可以獲得顯著提升,但其影響力和適用範圍較為有限。儘管難度高,改進 exp 算子收益太大了,必須要迎難而上。
通過我們的研究,發現在 exp prime 方向上的算法工作具有理論實現的可能性,並且有潛在的巨大收益。
因此,我們團隊決定將其適配到SPU 的 SEMI2K[1] 協議中。
我們實現了新版的 exp 計算方法,稱為 exp prime[2]。
然而,由於理論細節非常複雜,我們的改進在算法理論和工程實現上都進行了大量的微創新,因此我們無法直接預測 exp prime 在實際業務中的表現,特別是不確定它的精度和穩定性(是否能在較大範圍內完成高精度計算)。評估密態算子的性能本身非常困難。
MPC (Secure Multi Party Computation 多方安全計算) 算子設計需要多方通信和複雜的密碼學交互,並且受網絡條件的影響很大。
目前 SPU 的 MPC 算子基於定點數實現,因此新算子的精度是否能達到業務需求仍是未知數。
開發一個新的算子,特別是基於複雜理論和工程實踐的算子,業務團隊能否放心使用,計算時間能否減少,內存消耗是否會增加,模型精度是否會受到影響,適配新算法能否帶來顯著收益,投資回報率是否高,這些都是難以回答的問題。
與我們長期合作的業務團隊尚且對密態算子的性能缺乏直觀感受,而對密態計算感興趣的潛在合作方可能對這種性能評估更加陌生。
因此,本文系統地評估了 exp 算子的性能,旨在為當前的業務方和未來的合作方提供參考。本文的測評方法[3]將全部開源,以確保結果的可復現性。
測評定義
根據 MPC 算子的計算模式,以下維度能夠影響算子執行的耗時和消耗的資源,以及效果:
- 通訊量
- 輪數
- 內存
- 有效模擬範圍
- 誤差大小
- 耗時
在固定場景 SEMI2K FM128 下進行測試,因為 exp prime 目前僅支持該場景。
我們選擇了在 SPU 中現有的所有 exp 方法進行比較:
- exp pade 方法:初版高精度的 exp 模擬方法,強制啓用了下限和上限的 clamping。代號為 mod 1。
- exp taylor 方法:基於泰勒級數的模擬方法,可以通過調節迭代次數控制精度。迭代次數越多,性能越差。本次測試使用泰勒-8參數。預期性能大大優於 pade 方法,但精度較差,沒有 clamping。代號為 mod 2。
- exp prime 方法:最新實現的 exp 計算方法,clamping 可配置,默認啓用下限 clamping。代號為 mod 3。
注:
- clamping 指的是限制輸入數值的範圍。例如,合適的範圍為 [-10, 10],那麼輸入為-100時,我們將其處理為-10。
- clamping 在密態計算中開銷很大,應儘量避免。
- clamping 設置為一般訓練時能跑通的最快設置(經驗設置)。
結果前瞻
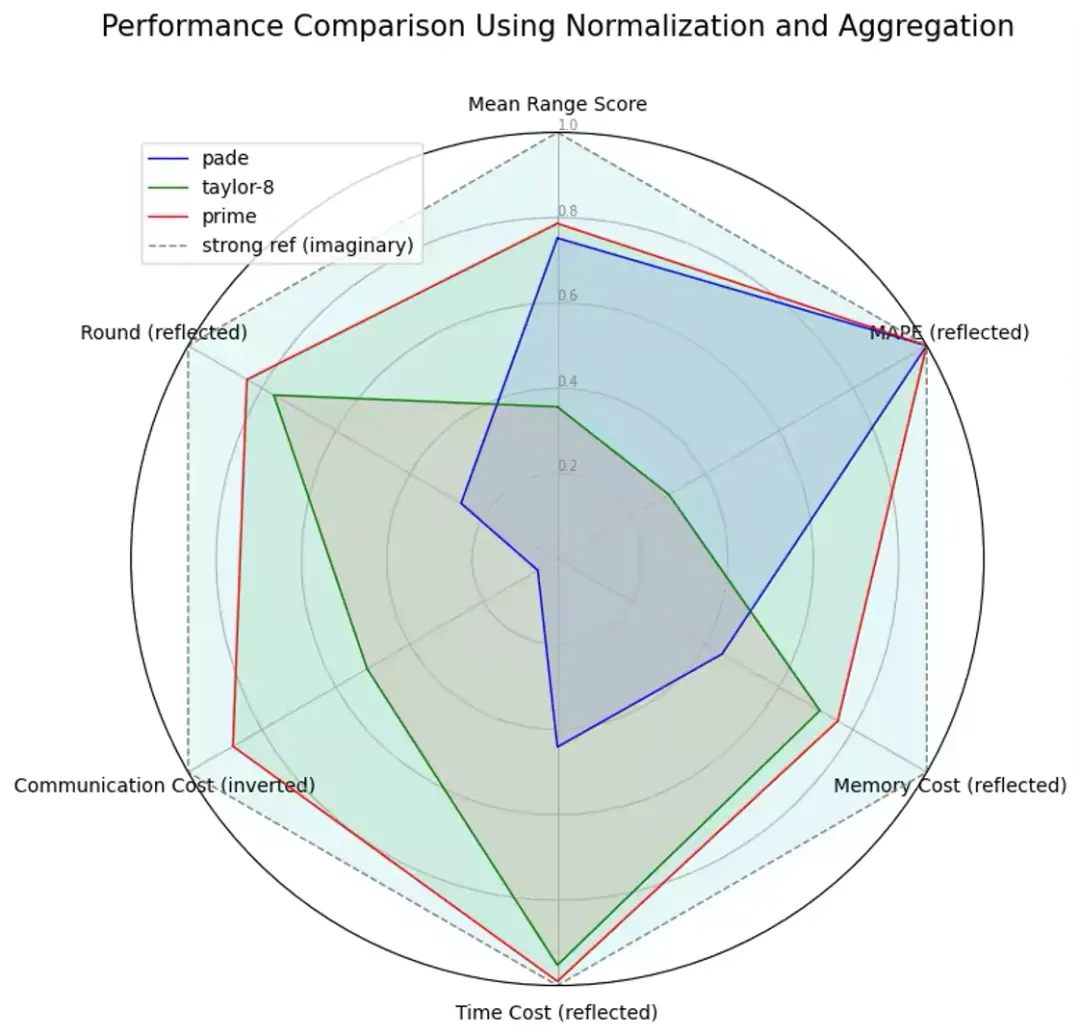
exp prime 能力六個測評維度上,都有優勢,屬於硬核突破。exp prime 在任何維度對於原有方法都具有優勢。
各維度分析
1. 通訊量
MPC 算子網絡性能的首要考慮因素。在實際業務落地中,MPC 算子的最大瓶頸在於帶寬需求。
由於計算過程中需要大量通信,增加 CPU 數量和性能並不能有效地減少計算耗時,而提升帶寬則可以。
提升帶寬的問題則在於,一般的業務場景下,帶寬並不像購買 CPU 那樣容易提升。因此,在其他條件不變的情況下,MPC算子的通訊量越低,其計算耗時越短,且帶寬越小,這種效應就越明顯。
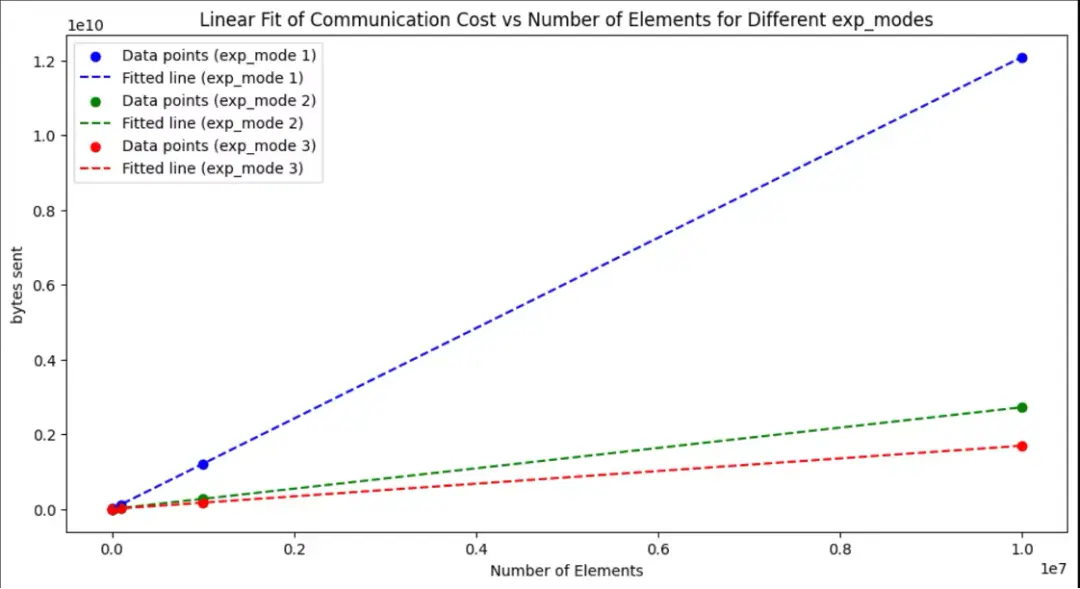
假設x為n個元素的數組,則exp(x)消耗的通訊量為平均通訊量乘以n。傳輸耗時與通訊量成反比。
例子:a, b, c 為 SEMI2K 下被秘密分享的3個數字。假如 pade 模式下 exp([a, b, c]) 消耗的通訊量為 1208 * 3 = 3624 bytes。假設帶寬為 每秒1024 bytes,那麼,不考慮其他計算,單單傳輸上述通訊量需要 3624/1024 = 3.54s。
結果
| exp mod | 平均通訊量 bytes |
|---|---|
| pade | 1208 |
| taylor-8 | 272 |
| prime | 169 |
數據 - exp 通訊量和輪數測量結果
num\_elements,exp\_mode,bytes_sent,round
10,1,12080,52
10,2,2720,17
10,3,1690,12
100,1,120800,52
100,2,27200,17
100,3,16900,12
1000,1,1208000,52
1000,2,272000,17
1000,3,169000,12
10000,1,12080000,52
10000,2,2720000,17
10000,3,1690000,12
100000,1,120800000,52
100000,2,27200000,17
100000,3,16900000,12
1000000,1,1208000000,52
1000000,2,272000000,17
1000000,3,169000000,12
10000000,1,12080000000,52
10000000,2,2720000000,17
10000000,3,1690000000,12
小結
exp prime (單方clip)通訊量比高精度pade 方法低7倍,為taylor-8方法的2/3, 是當前通訊量消耗最低的SEMI2K exp計算方法。網絡條件越惡劣,exp prime 優勢越大。
2. 輪數
MPC 算子網絡性能的次要因素。MPC 算子實現一次計算通常需要多次交互,如果網絡延遲高,則輪數越高的算子受延遲影響越大。
若網絡延遲為 10ms,exp(x) 通訊的輪數為 r。受延遲影響的傳輸耗時為 10r ms。但是不論 exp 要計算的元素數據量有多大,輪數是固定的。
結果
| exp mod | 輪數 |
|---|---|
| pade | 52 |
| taylor-8 | 17 |
| prime | 12 |
小結
exp prime (單方clip)通訊輪數比高精度pade 方法低4倍,為taylor-8方法的2/3, 是當前輪數消耗最低的SEMI2K exp計算方法。網絡條件越惡劣,exp prime 優勢越大。
3. 內存
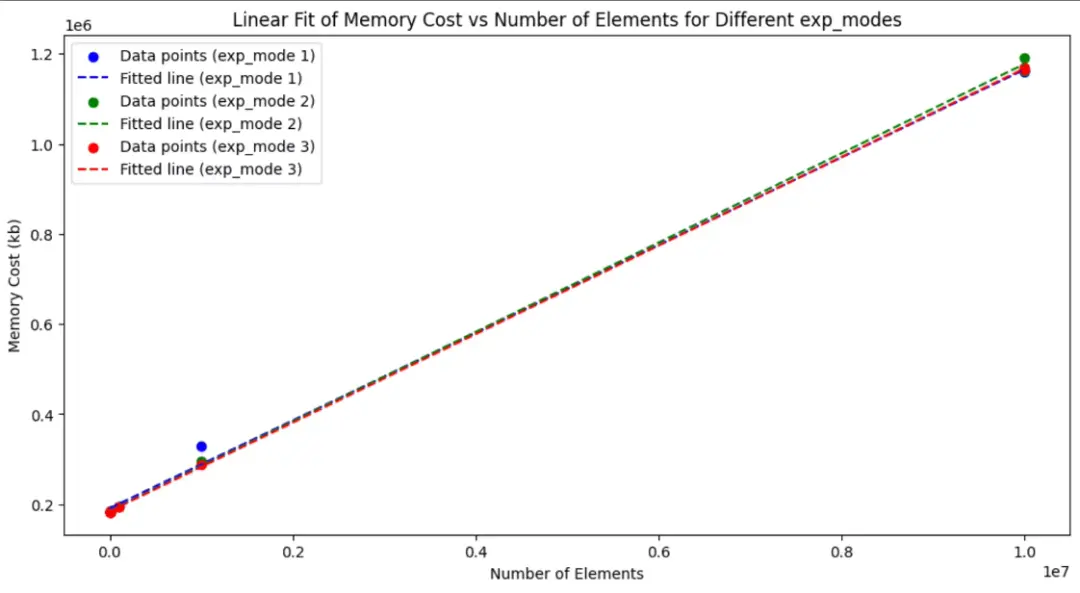
計算數據時候存在內存消耗, 如果最大內存(Peak Memory) 超過了計算機的 RAM, 則會報錯終止進程。
我們對於內存消耗建模為 y = a n+ b;y 為內存峯值,n 為需要計算的元素數量,a 為平均一個元素的內存消耗,b 為程序與元素數量無關的內存開銷。
結果
| exp mod | 平均內存消耗(kb) | 其他內存開銷(kb) |
|---|---|---|
| pade | 0.1 | 191083 |
| taylor-8 | 0.1 | 185784 |
| prime | 0.1 | 184807 |
數據 - exp 內存消耗測量結果
num\_elements,exp\_mode,mem_cost(kb)
10,1,183296
10,2,183808
10,3,183808
100,1,183296
100,2,183808
100,3,183808
1000,1,183296
1000,2,183808
1000,3,183296
10000,1,183808
10000,2,184832
10000,3,184320
100000,1,195756
100000,2,194716
100000,3,194968
1000000,1,329248
1000000,2,294868
1000000,3,288316
10000000,1,1160468
10000000,2,1161496
10000000,3,1168996
10000000,1,1164852
10000000,2,1191800
10000000,3,1164632
小結
exp prime 邊際內存消耗和pade, taylor 相當, 總消耗不高於前兩種方法。
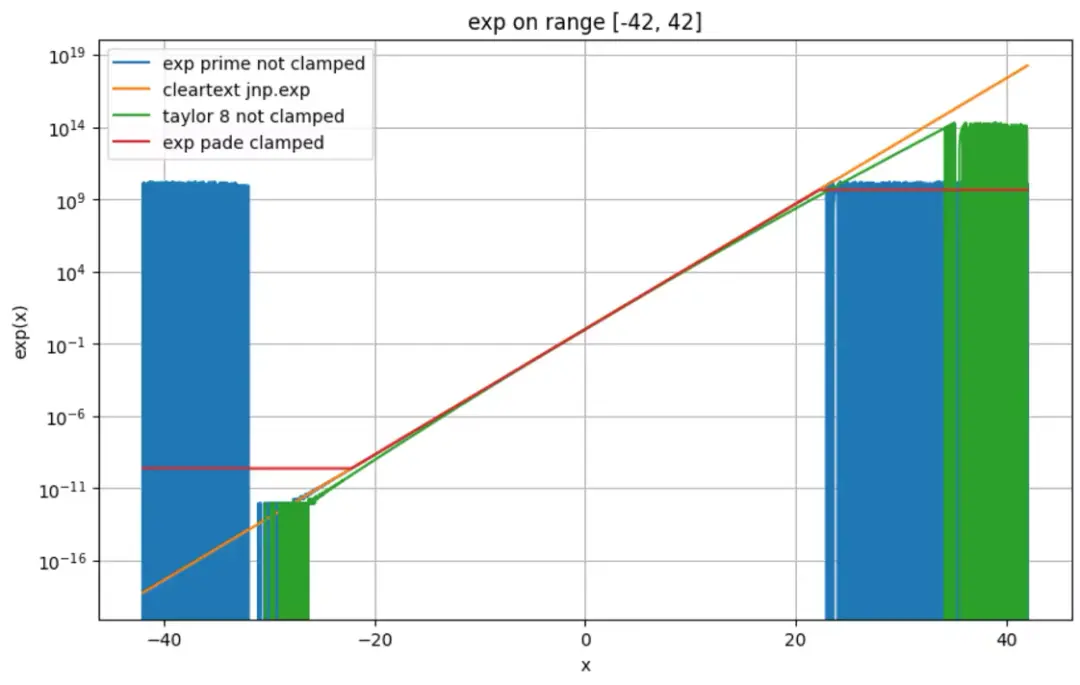
4. 有效模擬範圍
MPC 下的 exponential 算子和明文相比有差距。若 exp(x) MPC 計算的模擬誤差和明文差距不大,則在 MPC 下計算 exp(x) 是有實際意義的,若誤差過大比如則不能視為有效的模擬計算。
如果告訴你一個算法,速度很快,精度很高,但是它要求輸入必須是[-10, 10]之間的數字,那麼它是一個好算法嗎?如果輸入範圍以外的數字,答案會錯得離譜。
例如,業務場景下輸入的數字範圍是[-10, 30]怎麼辦?業務大概率不能使用這個算法。有效範圍越大,可運用的業務範圍就越廣,場景就越多。
默認參數下的有效模擬範圍:
對於 [-40,40] 中等距採樣10000個數,精準模擬的數 / 10000 = 精準模擬的比例。
精準模擬的標準:
絕對誤差 Absolute Error = |x_true - x|
相對誤差 Absolute Percentage Error : |x\_true - x| / |x\_true|
下表中AE < 5 的含義是 絕對誤差< 5 視作精準模擬。下表中的數值為精準模擬比例,明文參考值為1。
結果
exp prime 平均有效模擬比例為0.629, 在長度為[-40, 40]的範圍內能有效模擬接近2/3的數值。有效範圍高於exp pade 方法,大大高於taylor-8方法。
但是一旦不在有效模擬範圍,無clamping exp prime 的誤差也許會大到離譜。
數據
| exp mode | ape < 5% | ape < 1% | ape < 0.05% | ae < 5 | ae < 1 | ae < 0.05 | mean range score |
|---|---|---|---|---|---|---|---|
| prime | 0.6177 | 0.5981 | 0.5607 | 0.7074 | 0.6925 | 0.6561 | 0.629 |
| taylor-8 | 0.1285 | 0.0568 | 0.0126 | 0.5595 | 0.5458 | 0.5242 | 0.285 |
| pade | 0.5557 | 0.5548 | 0.5439 | 0.6811 | 0.6624 | 0.626 | 0.602 |
一旦不在有效模擬範圍,無 clamping exp prime 的誤差也許會大到離譜。根據該結果,我們在工程實踐中使用了可配置的 clamping, 本文所有測評都是基於默認參數啓用lower clamping 完成的 (因為常用輸入總是超過下界,而不超過上界)。
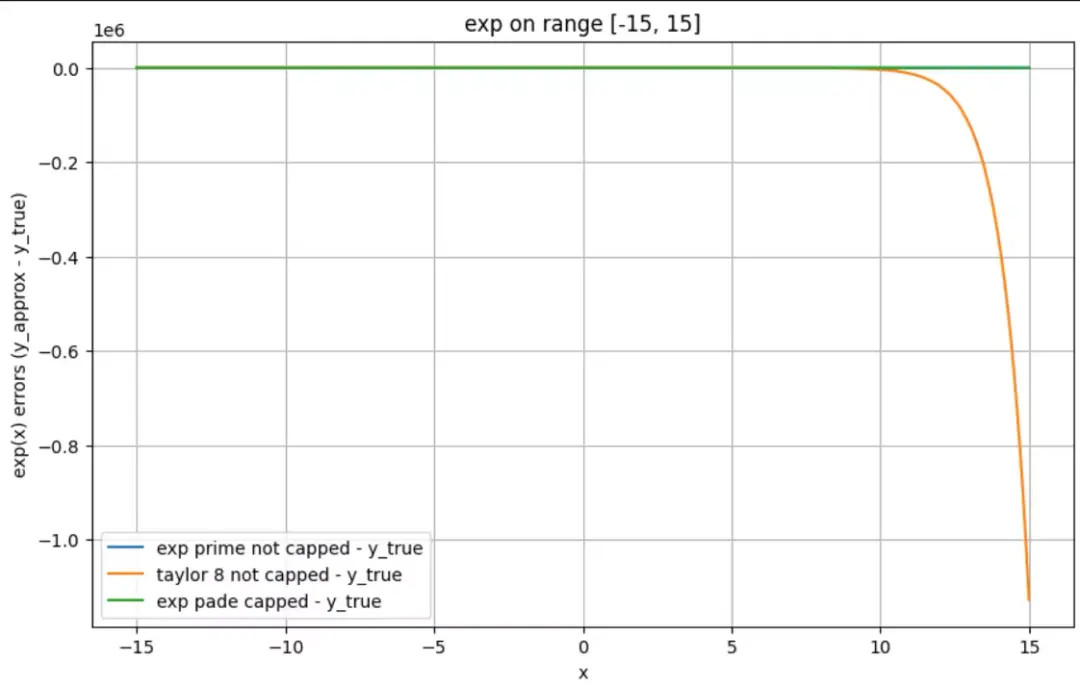
taylor-8 看起來模擬範圍更大?其問題是表面看起來差距不大,但是實際誤差已經很大了(上圖為 log scale)。上圖中 taylor-8, ape < 5% 的範圍可能比肉眼感覺的要小的多。
通過下圖 exp 和明文的誤差來演示這一點,注意 y軸 為 10^6 。
小結
exp prime 使用場景大概率廣於pade和taylor-8 算法,如果過去taylor和pade方法能滿足需求,則可以放心使用exp prime 方法。
大部分場景下使用默認參數即可,輸入過大時需要啓用upper clamping。
5. 誤差大小
即使所有計算都在常用且能夠有效模擬的範圍內進行,我們仍然希望 exp 計算的誤差儘可能低,以接近明文計算的精度。
在離線 MPC 訓練和在線聯邦預測的場景下,在線預測使用的是明文計算的 exp。如果誤差較大,那麼在線預測與離線訓練之間的差異也會隨之增大。
想象一下,在一個二分類場景中,你訓練了一個AUC達0.97的模型,為了將AUC從0.94提升到0.97,你花費了大量精力進行優化(離線預測測試)。
然而,僅僅是訓練和預測之間的exp計算誤差就可能使在線預測的AUC降到0.965。更糟糕的是,你本可以達到0.98的AUC,但由於MPC exp計算誤差,你只能達到0.97的AUC。
精度誤差可以導致AUC下降0.025!這正是使用MPC建模的算法工程師在聯合建模效果上的一大困擾。因此,我們一定希望exp計算的誤差越低越好!
結果
exp prime 的平均絕對誤差, 平均相對誤差,平均誤差平方都是現有方法中最低的。比過去高精度的方法精度要高1-3個數量級。
數據
在x 為[-20, 20] 的數字中我們比較 exp模擬的 Mean Squared Error, Mean Absolute Error 和 Mean Absolute Percentage Error
| exp mode | mse | mae | mape |
|---|---|---|---|
| prime | 1075.37 | 6.12 | 3.898e-06 |
| taylor-8 | 759747514271408.9 | 5943857.74 | 0.209 |
| pade | 1322195.69 | 153.83 | 1.605e-05 |
小結
exp prime 的精度最高,十分接近明文,能滿足絕大部分場景的精度需要,遠超過去方法。
6. 耗時
計算耗時是算法工程師、業務方都高度關注的一個指標,也是過去性能benchmark中唯一各方關注的指標,打榜就靠它了。
- 對於算法工程師來説,如果跑一個聯合建模算法要8小時,一條只能調參1次,如果聯合建模耗時5小時,那麼一天能夠調參2次,效率提高1倍。
- 對於業務來説,以前更新一次數據,完全新的聯合建模要15天,現在如果能10天上線,那麼提早5天上線,多創造的這部分價值就是收益。可以想象一下,若有幾十個機構,平均每半年就要更新一次更新數據聯合建模,服務數億級別的客户,降低耗時創造的價值是巨大的。
但是,MPC 場景的耗時測量受很大的網絡參數影響。LAN 網絡下,所有 MPC 計算好像都挺快,WAN 網絡下,MPC 計算耗時能長到令人懷疑人生。
我們採取以下場景進行耗時評測:
net level specification
0) net_rate="100000mbit" net_latency="0ms";;
1) net_rate="1000mbit" net_latency="1ms";;
2) net_rate="100mbit" net_latency="10ms";;
3) net_rate="10mbit" net_latency="100ms";;
我們對於時間消耗建模 為 y = a n+ b,y 為耗時,n 為需要計算的元素數量,a 為平均一個元素的時間消耗 (邊際耗時),b 為程序與元素數量無關的時間開銷。
結果
net level 2,100Mb 帶寬,10ms 延時,是一個最常用的評測場景。
| exp mod | net_level 2 邊際耗時(s) |
|---|---|
| pade | 12.065e-05 |
| taylor-8 | 2.86e-05 |
| prime | 2.18e-05 |
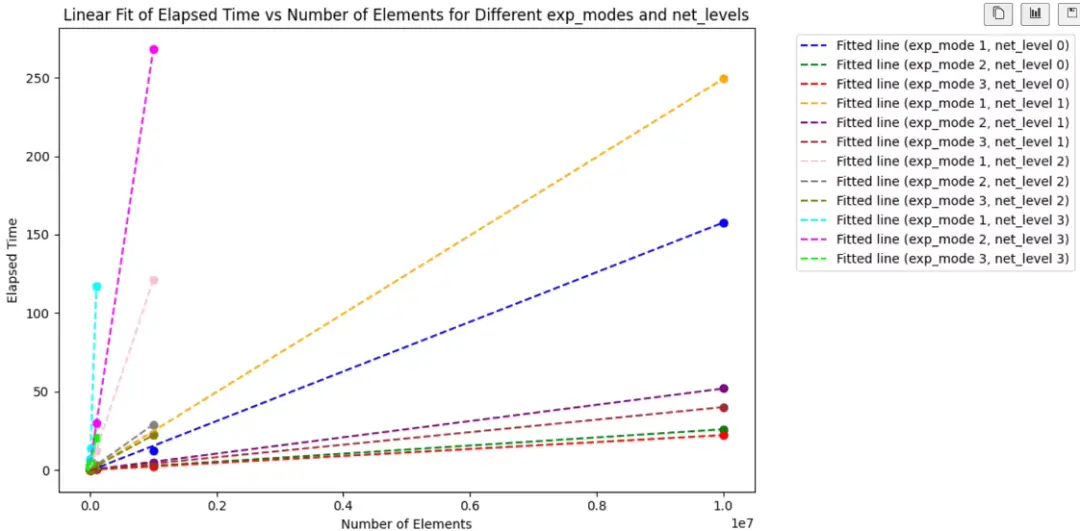
其他耗時可參考下圖
數據 - exp 時間消耗測量結果
num\_elements,exp\_mode,elapsed\_time,net\_level
10000,3,0.10899242595769465,0
100000,1,1.5562007201369852,0
100000,2,0.3806668110191822,0
100000,3,0.36923978198319674,0
1000000,1,12.413455325877294,0
1000000,2,2.3289378818590194,0
1000000,3,2.0647744049783796,0
10000000,1,157.84879399999045,0
10000000,2,25.858311526011676,0
10000000,3,22.179473932133988,0
10,1,0.13805793807841837,1
10,2,0.09943982097320259,1
10,3,0.10655678412877023,1
100,1,0.15299400803633034,1
100,2,0.10206696693785489,1
100,3,0.09619212592951953,1
1000,1,0.17369073489680886,1
1000,2,0.11150461691431701,1
1000,3,0.10390148684382439,1
10000,1,0.3839655520860106,1
10000,2,0.1682215000037104,1
10000,3,0.17196061299182475,1
100000,1,2.7040774549823254,1
100000,2,0.6501772250048816,1
100000,3,0.5786988700274378,1
1000000,1,23.041077816160396,1
1000000,2,4.713096359046176,1
1000000,3,3.8042779518291354,1
10000000,1,249.34486315306276,1
10000000,2,51.86276936996728,1
10000000,3,40.010631297016516,1
10,1,0.7347624329850078,2
10,2,0.3620553209912032,2
10,3,0.335803555091843,2
100,1,0.7282703381497413,2
100,2,0.3660985380411148,2
100,3,0.3254895710851997,2
1000,1,0.8166786769870669,2
1000,2,0.441350911045447,2
1000,3,0.3981817150488496,2
10000,1,1.6240983819589019,2
10000,2,0.6257592940237373,2
10000,3,0.5846053399145603,2
100000,1,12.155489874072373,2
100000,2,3.043655260000378,2
100000,3,2.4608653138857335,2
1000000,1,121.23415710008703,2
1000000,2,28.960522881010547,2
1000000,3,22.12015020288527,2
10,1,6.521644555963576,3
10,2,2.888359455158934,3
10,3,2.4858575160615146,3
100,1,6.515798039967194,3
100,2,2.910730817820877,3
100,3,2.4944541668519378,3
1000,1,7.144702007062733,3
1000,2,3.7519471780397,3
1000,3,3.115263829007745,3
10000,1,13.943796247942373,3
10000,2,5.395836747949943,3
10000,3,4.7630465012043715,3
100000,1,117.0330176721327,3
100000,2,29.69434425421059,3
100000,3,20.770910662133247,3
1000000,2,268.1107207580935,3
小結
exp prime 邊際耗時在所有場景下都是最低的,且網絡條件越惡劣,相對優勢越大。應證了之前根據網絡條件的推理。
總體分析
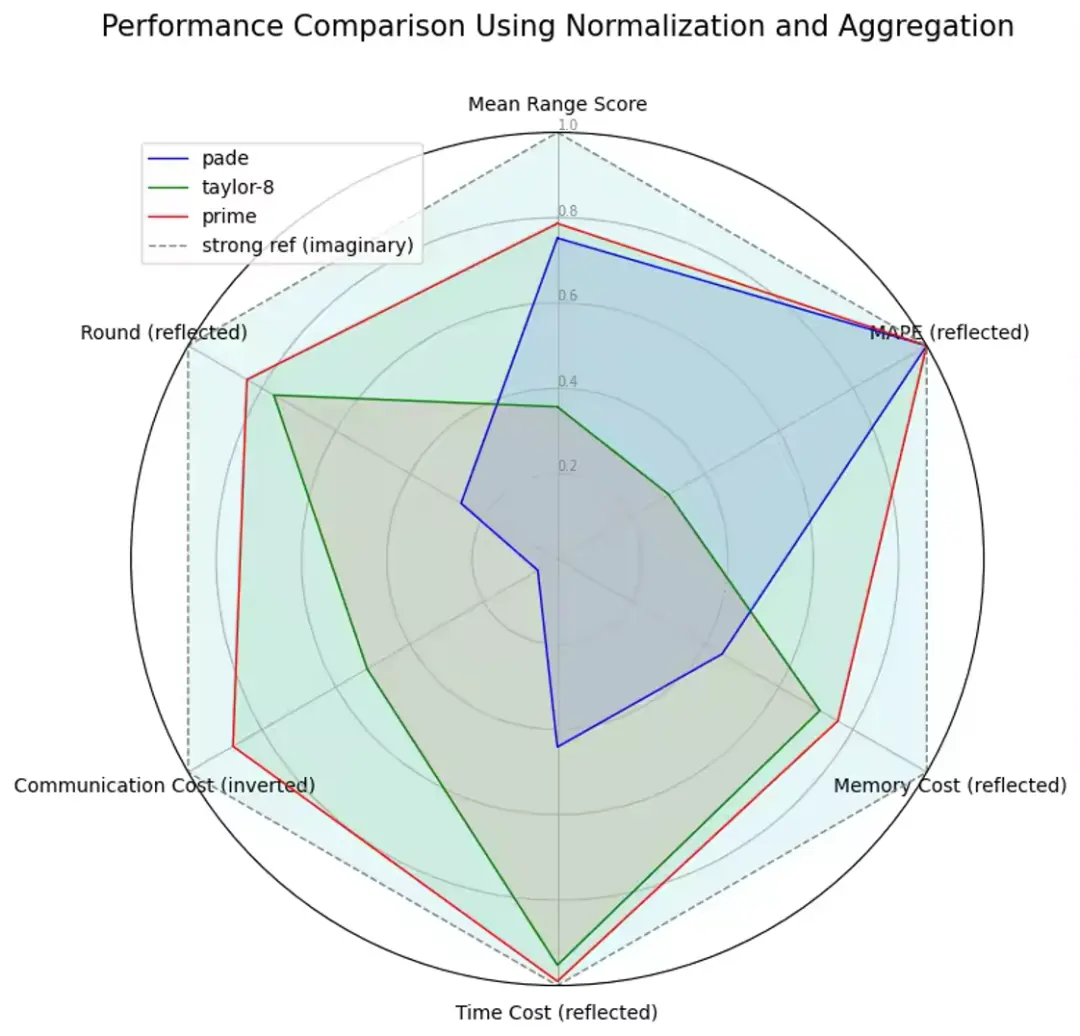
各個維度上,exp prime 都是目前最優的指數計算方法。
我們選取了各個維度的指標,並進行了轉換處理,以可視化其相對優勢。具體而言:
- 通訊量:採用 ( 1/邊際通訊量 ) 的標準來打分,通訊量越高分數越低。
- 輪數:採用(-輪數)的標準來打分,輪數越低分數越高。
- 有效模擬範圍:採用平均有效比例的標準來打分,平均有效比例越高分數越高。
- 誤差大小:採用 (-MAPE) 的標準來打分,MAPE越高分數越低。
- 內存:採用 (-邊際內存消耗}) 的標準來打分,邊際內存消耗越高分數越低。
- 耗時:採用 (-net_level 2 邊際耗時) 的標準來打分,邊際耗時越高分數越低。
總結
exp prime 新方法在各方面的模擬計算性能均優於之前的方法,適用範圍更廣,效果更好,耗時更低,同時保持了相同的安全性。
在不做任何妥協的情況下,exp prime 顯著提升了 exp 的性能,精度和有效模擬範圍也大大超出了預期。
作為一個基礎算子,exponential 在眾多算法中都扮演着重要角色。無論是樹模型還是線性模型,無論是聯合分析還是 MPC 大模型訓練,只要算法中使用了 exp prime,都能獲得顯著的性能提升和表現改善,預計將創造巨大的價值。
復現
exp prime 方法已經遞交了專利,且相應代碼已經開源,暫時實驗性地支持了 SEMI2K FM128 場景。
[1] SPU SEMI2K 協議:(歡迎 star 🌟 ,關注更多技術更新動態~
https://github.com/secretflow/spu/blob/main/src/libspu/mpc/semi2k
[2] exp prime 方法代碼:
https://github.com/secretflow/spu/blob/main/libspu/mpc/semi2k/exp.h
[3] 測評思路:具體流程 -- 起 Docker、限制帶寬、RUN、收集數據、分析
https://github.com/secretflow/spu/tree/atc23_ae
參考
該方法參考了以下論文進行改造實現:
- 《Secure Poisson Regression》:https://www.usenix.org/system/files/sec22summer_kelkar.pdf
- 《A Framework for Secure Two-Party Computation through Efficient Modulus Conversion and Mixed-Mode Protocols》 (no publication yet)