概述

圖是一種較為複雜的非線性結構。 為啥説其較為複雜呢？

根據前面的內容，我們知道：

• 線性數據結構的元素滿足唯一的線性關係，每個元素(除第一個和最後一個外)只有一個直接前趨和一個直接後繼。
• 樹形數據結構的元素之間有着明顯的層次關係。

但是，圖形結構的元素之間的關係是任意的。

何為圖呢？ 簡單來説，圖就是由頂點的有窮非空集合和頂點之間的邊組成的集合。通常表示為：G(V,E)，其中，G 表示一個圖，V 表示頂點的集合，E 表示邊的集合。

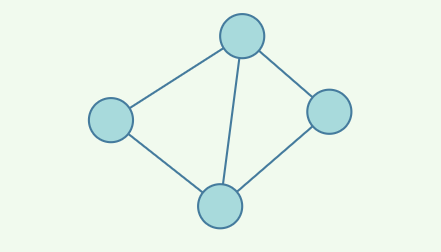
下圖所展示的就是圖這種數據結構

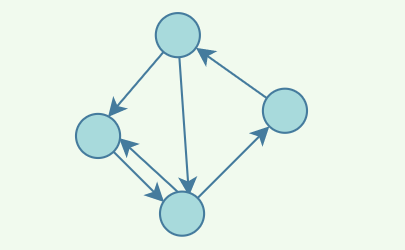
同時圖⼜分為有向圖與⽆向圖，上⾯的是⽆向圖，因為邊沒有指明⽅向，只是表示兩者關聯關係，⽽有向圖則是這樣：

圖在我們日常生活中的例子很多！比如我們在社交軟件上好友關係就可以用圖來表示。

圖的基本概念

頂點

圖中的數據元素，我們稱之為頂點，圖至少有一個頂點（非空有窮集合）

對應到好友關係圖，每一個用户就代表一個頂點。

邊

頂點之間的關係用邊表示。

對應到好友關係圖，兩個用户是好友的話，那兩者之間就存在一條邊。

度

度表示一個頂點包含多少條邊，在有向圖中，還分為出度和入度，出度表示從該頂點出去的邊的條數，入度表示進入該頂點的邊的條數。

對應到好友關係圖，度就代表了某個人的好友數量。

無向圖和有向圖

邊表示的是頂點之間的關係，有的關係是雙向的，比如同學關係，A 是 B 的同學，那麼 B 也肯定是 A 的同學，那麼在表示 A 和 B 的關係時，就不用關注方向，用不帶箭頭的邊表示，這樣的圖就是無向圖。

有的關係是有方向的，比如父子關係，師生關係，微博的關注關係，A 是 B 的爸爸，但 B 肯定不是 A 的爸爸，A 關注 B，B 不一定關注 A。在這種情況下，我們就用帶箭頭的邊表示二者的關係，這樣的圖就是有向圖。

無權圖和帶權圖

對於一個關係，如果我們只關心關係的有無，而不關心關係有多強，那麼就可以用無權圖表示二者的關係。

對於一個關係，如果我們既關心關係的有無，也關心關係的強度，比如描述地圖上兩個城市的關係，需要用到距離，那麼就用帶權圖來表示，帶權圖中的每一條邊一個數值表示權值，代表關係的強度。

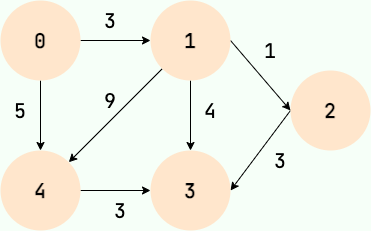
下圖就是一個帶權有向圖。

圖的存儲

鄰接矩陣存儲

鄰接矩陣將圖用二維矩陣存儲，是一種較為直觀的表示方式。

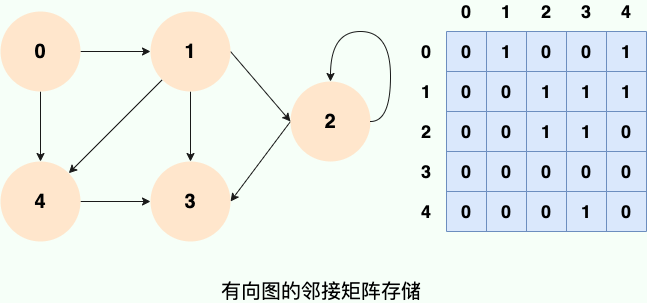
如果第 i 個頂點和第 j 個頂點之間有關係，且關係權值為 n，則 A[i][j]=n 。

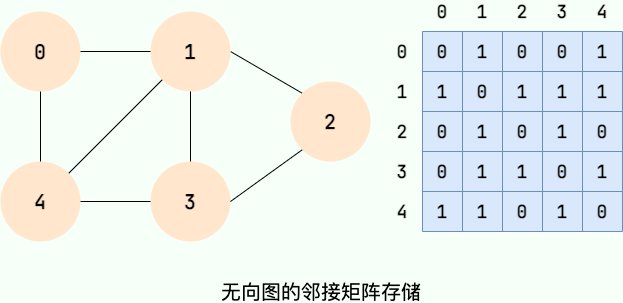
在無向圖中，我們只關心關係的有無，所以當頂點 i 和頂點 j 有關係時，A[i][j]=1，當頂點 i 和頂點 j 沒有關係時，A[i][j]=0。如下圖所示：

值得注意的是：無向圖的鄰接矩陣是一個對稱矩陣，因為在無向圖中，頂點 i 和頂點 j 有關係，則頂點 j 和頂點 i 必有關係。

鄰接矩陣存儲的方式優點是簡單直接（直接使用一個二維數組即可），並且，在獲取兩個定點之間的關係的時候也非常高效（直接獲取指定位置的數組元素的值即可）。但是，這種存儲方式的缺點也比較明顯，那就是比較浪費空間，

鄰接表存儲

針對上面鄰接矩陣比較浪費內存空間的問題，誕生了圖的另外一種存儲方法—鄰接表 。

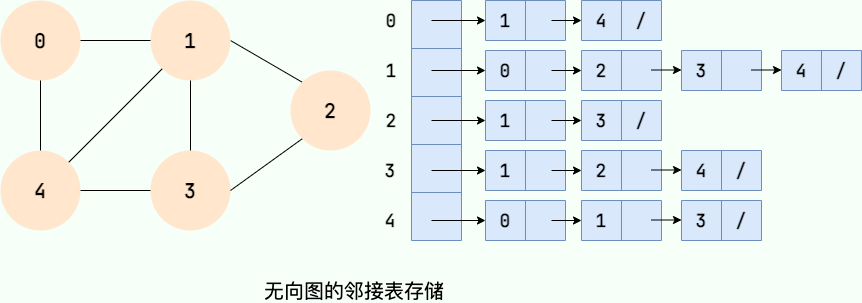
鄰接鏈表使用一個鏈表來存儲某個頂點的所有後繼相鄰頂點。對於圖中每個頂點 Vi，把所有鄰接於 Vi 的頂點 Vj 鏈成一個單鏈表，這個單鏈表稱為頂點 Vi 的 鄰接表。如下圖所示：

大家可以數一數鄰接表中所存儲的元素的個數以及圖中邊的條數，你會發現：

• 在無向圖中，鄰接表元素個數等於邊的條數的兩倍，如左圖所示的無向圖中，邊的條數為 7，鄰接表存儲的元素個數為 14。
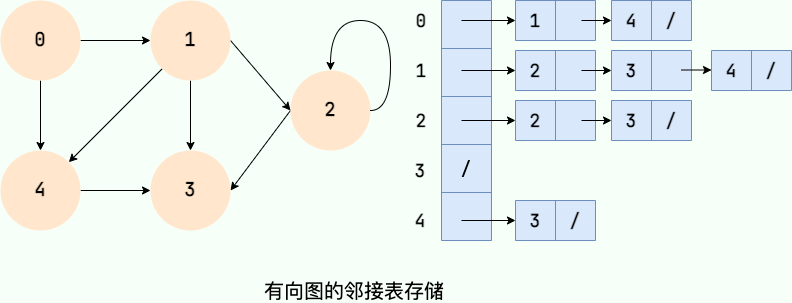
• 在有向圖中，鄰接表元素個數等於邊的條數，如右圖所示的有向圖中，邊的條數為 8，鄰接表存儲的元素個數為 8。

圖的搜索

圖⾥⾯遍歷⼀般分為⼴度優先遍歷和深度優先遍歷，⼴度優先遍歷是指優先遍歷與當前頂點直接相關的頂點，⼀般藉助隊列實現。⽽深度優先遍歷則是往⼀個⽅向⼀直⾛到不能再⾛，有點不撞南牆不回頭的意思，⼀般使⽤遞歸實現。

廣度優先搜索

廣度優先搜索就像水面上的波紋一樣一層一層向外擴展，如下圖所示：

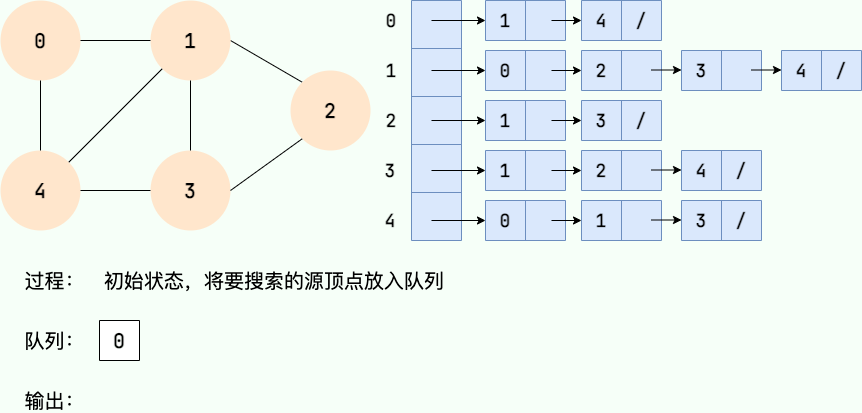
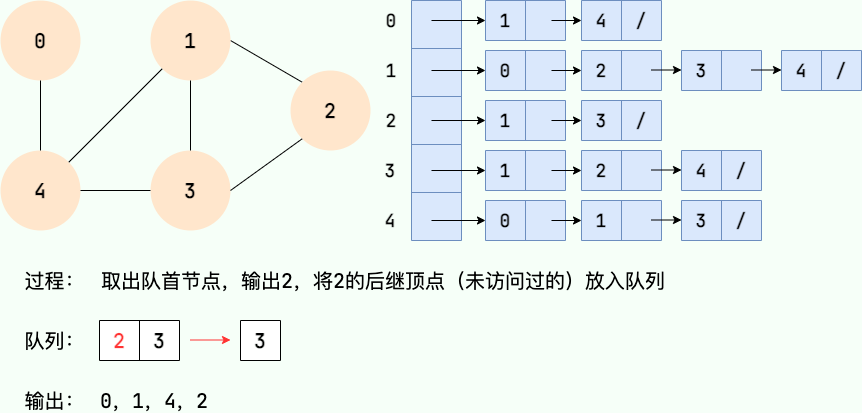
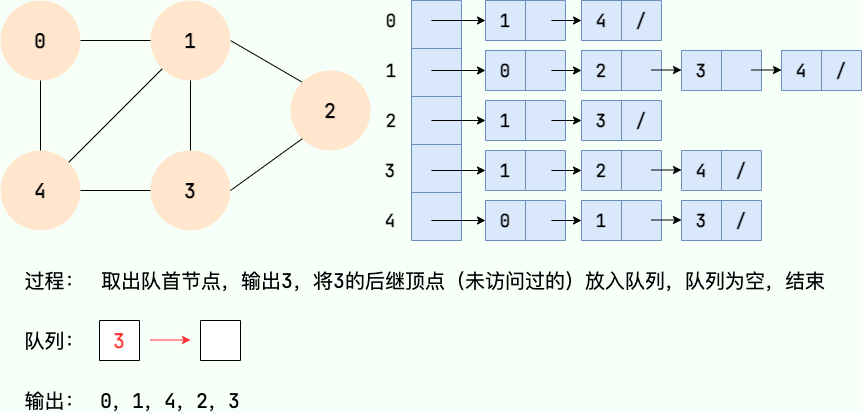
廣度優先搜索的具體實現方式用到了之前所學過的線性數據結構——隊列 。具體過程如下圖所示：

第 1 步：

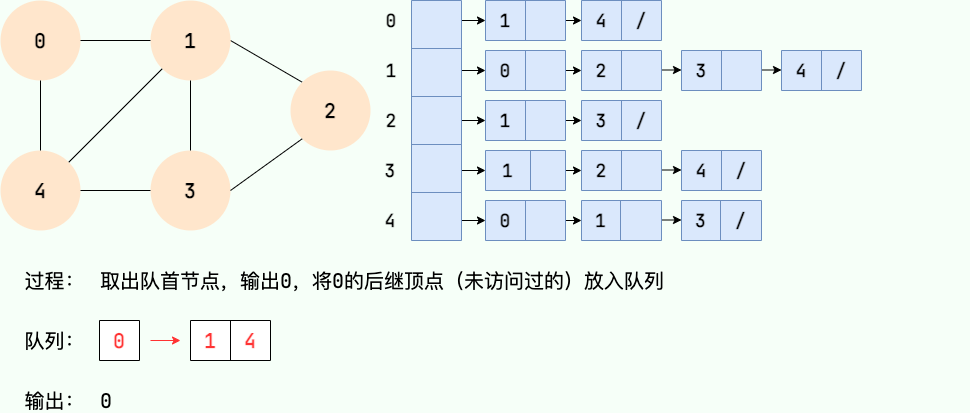
第 2 步：

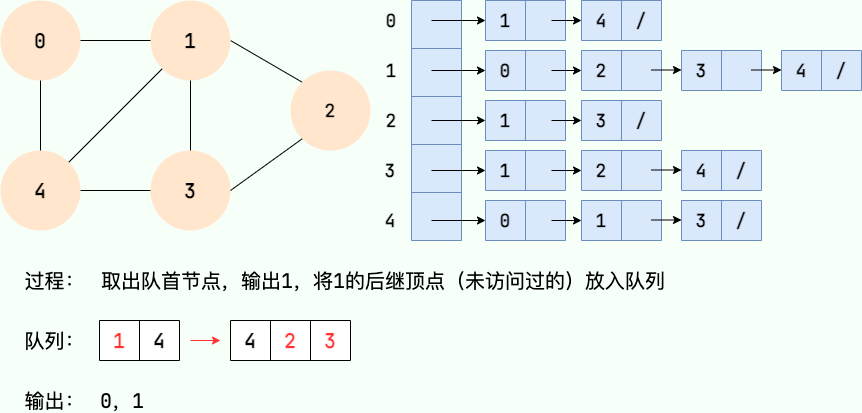
第 3 步：

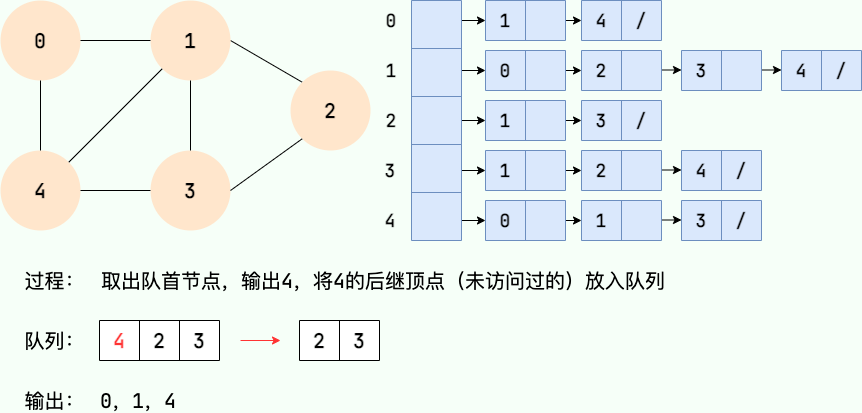
第 4 步：

第 5 步：

第 6 步：

深度優先搜索

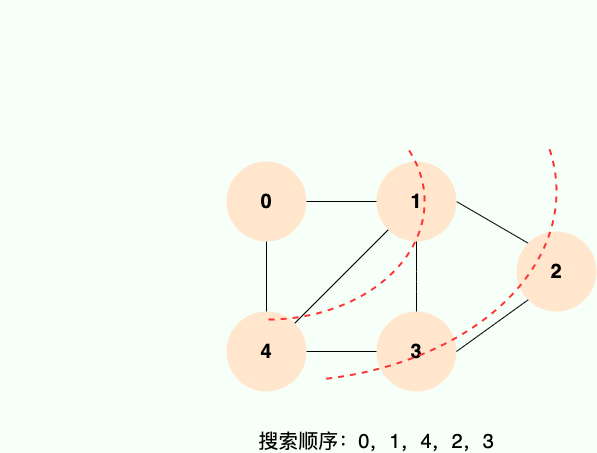
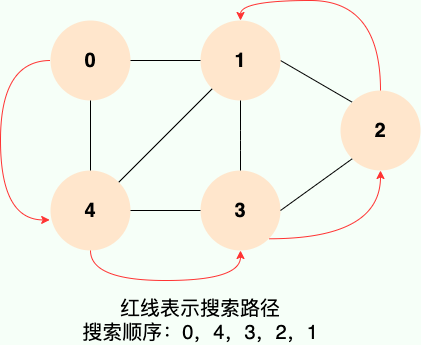
深度優先搜索就是“一條路走到黑”，從源頂點開始，一直走到沒有後繼節點，才回溯到上一頂點，然後繼續“一條路走到黑”，如下圖所示：

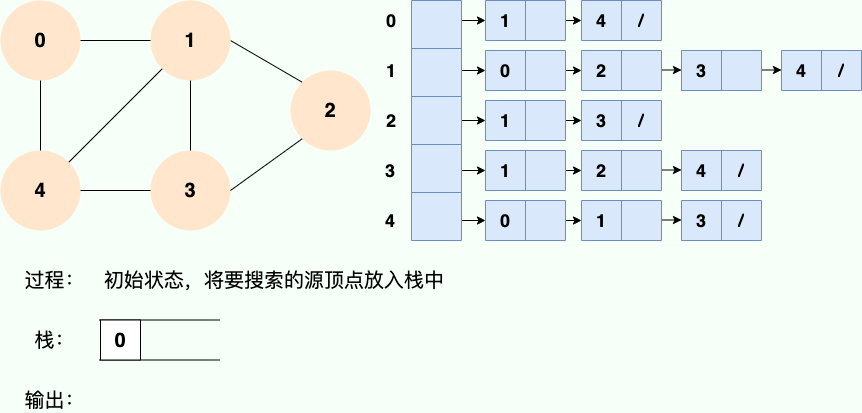
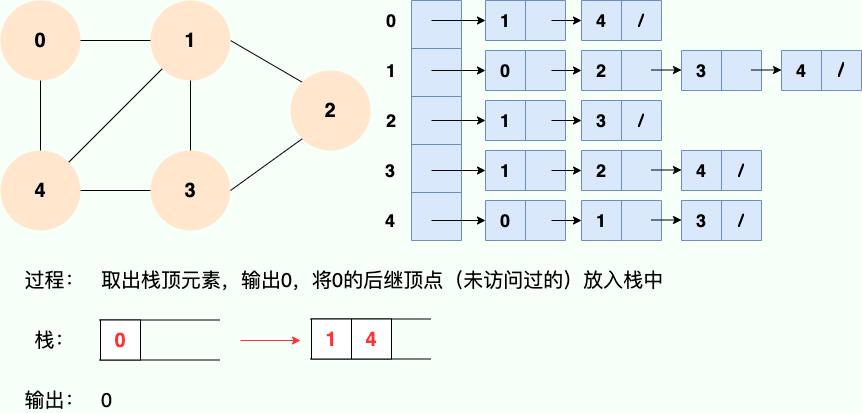
和廣度優先搜索類似，深度優先搜索的具體實現用到了另一種線性數據結構——棧 。具體過程如下圖所示：

第 1 步：

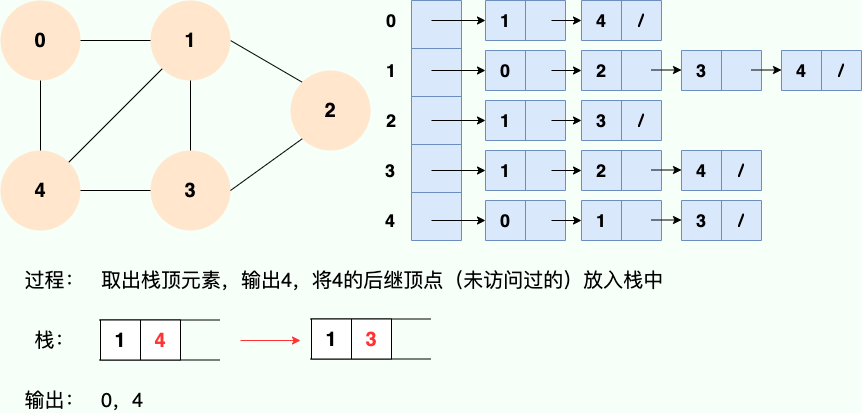
第 2 步：

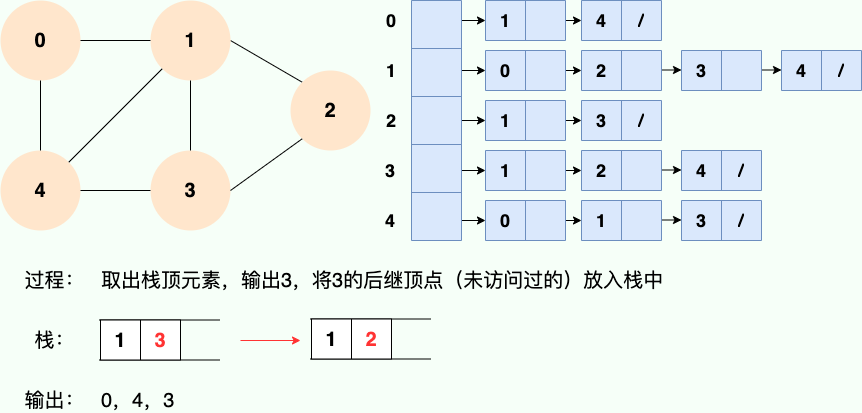
第 3 步：

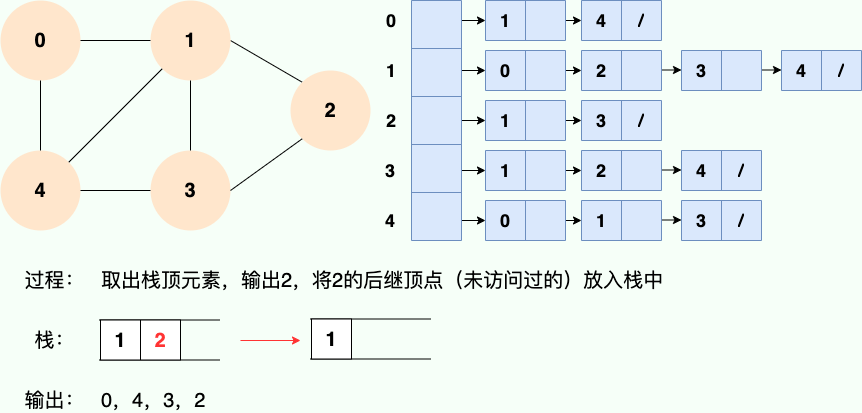
第 4 步：

第 5 步：

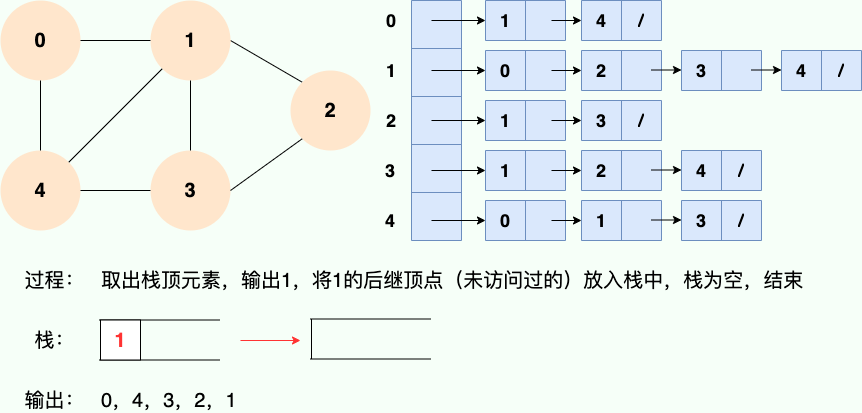
第 6 步：

算法框架如下：

// 記錄被遍歷過的節點
boolean[] visited;
// 記錄從起點到當前節點的路徑
boolean[] onPath;

/* 圖遍歷框架 */
void traverse(Graph graph, int s) {
    if (visited[s]) return;
    // 經過節點 s，標記為已遍歷
    visited[s] = true;
    // 做選擇：標記節點 s 在路徑上
    onPath[s] = true;
    for (int neighbor : graph.neighbors(s)) {
        traverse(graph, neighbor);
    }
    // 撤銷選擇：節點 s 離開路徑
    onPath[s] = false;
}