題⽬描述

給定⼀個數組和滑動窗⼝的⼤⼩，找出所有滑動窗⼝⾥數值的最⼤值。例如，如果輸⼊數組 {2,3,4,2,6,2,5,1} 及滑動窗⼝的⼤⼩ 3 ，那麼⼀共存在 6 個滑動窗⼝，他們的最⼤值分別為 {4,4,6,6,6,5} ；

針對數組 {2,3,4,2,6,2,5,1} 的滑動窗⼝有以下6個： {[2,3,4],2,6,2,5,1} ， {2,[3,4,2],6,2,5,1} ， {2,3,[4,2,6],2,5,1} ， {2,3,4, [2,6,2],5,1} ， {2,3,4,2,[6,2,5],1} ， {2,3,4,2,6,[2,5,1]} 。 窗⼝⼤於數組⻓度的時候，返回空。

思路及解答

暴力法

遍歷每個可能的窗口起始位置，計算窗口內的最大值

public class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        // 處理邊界情況
        if (nums == null || nums.length == 0 || k <= 0 || k > nums.length) {
            return new int[0];
        }
        
        int n = nums.length;
        int[] result = new int[n - k + 1]; // 結果數組
        
        // 遍歷每個窗口的起始位置
        for (int i = 0; i <= n - k; i++) {
            int max = Integer.MIN_VALUE;
            
            // 計算當前窗口內的最大值
            for (int j = i; j < i + k; j++) {
                if (nums[j] > max) {
                    max = nums[j];
                }
            }
            result[i] = max;
        }
        
        return result;
    }
}

• 時間複雜度：O(n×k)，需要處理n-k+1個窗口，每個窗口需要k次比較
• 空間複雜度：O(1)，除結果數組外只使用常數空間

雙端隊列法（最優解）

⾸先進⾏⾮空判斷，以及數組⻓度是否不為 0 ，是否不⼩於窗⼝⻓度。

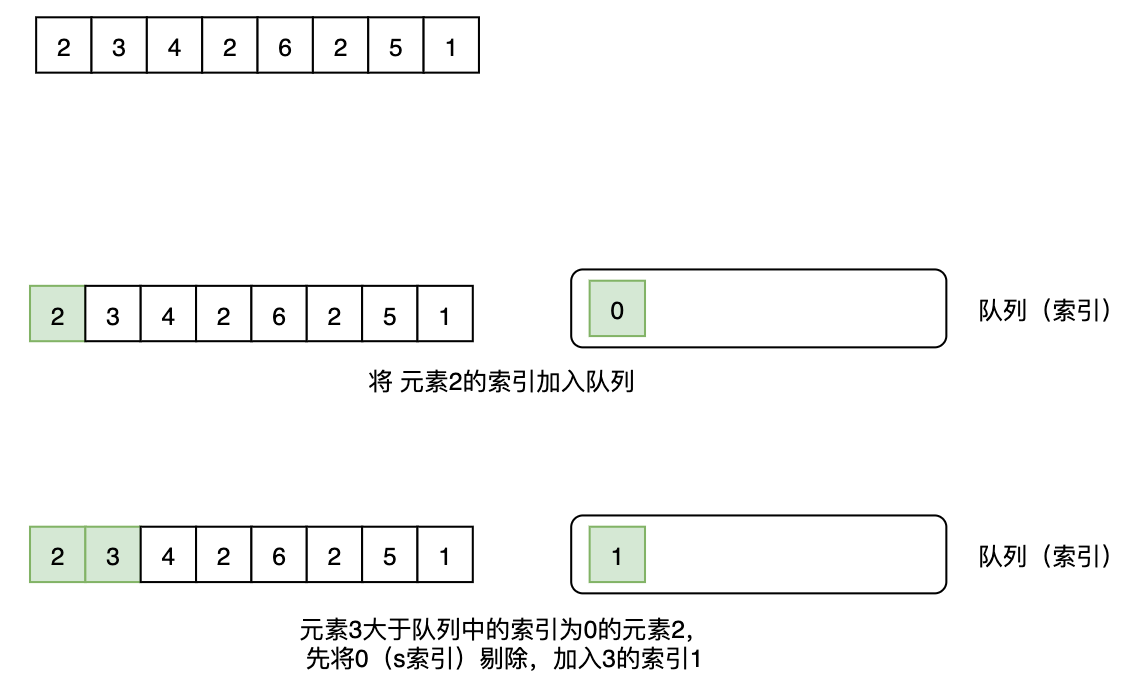
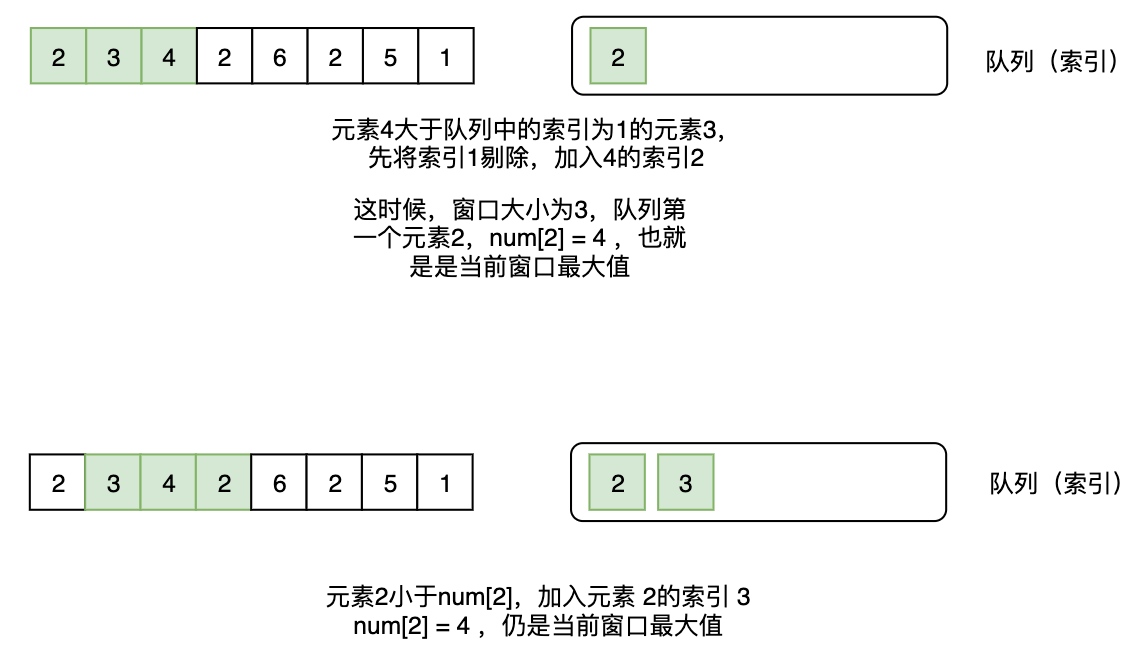
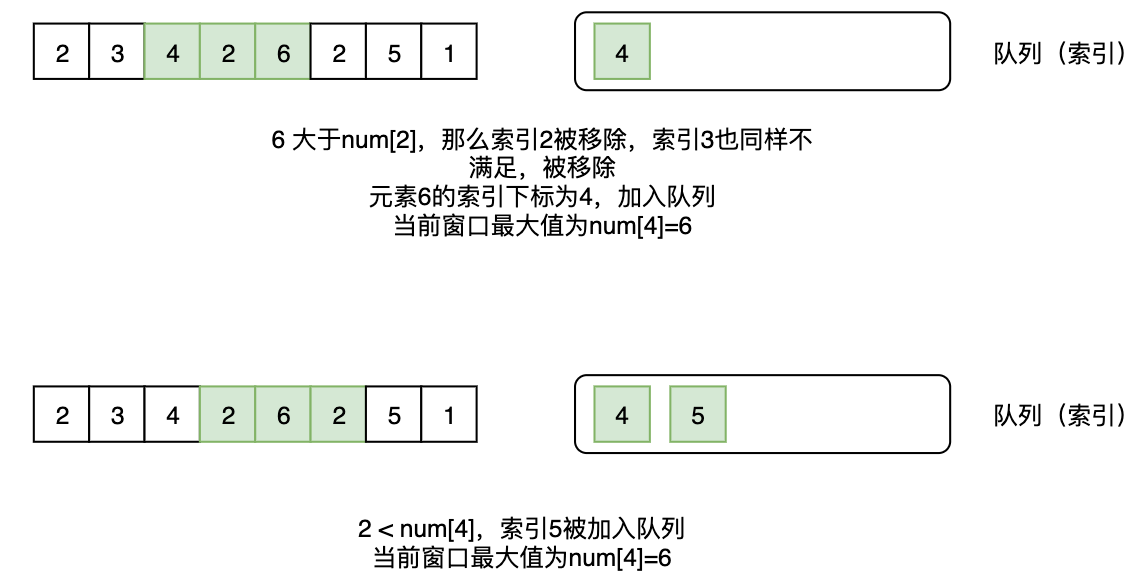
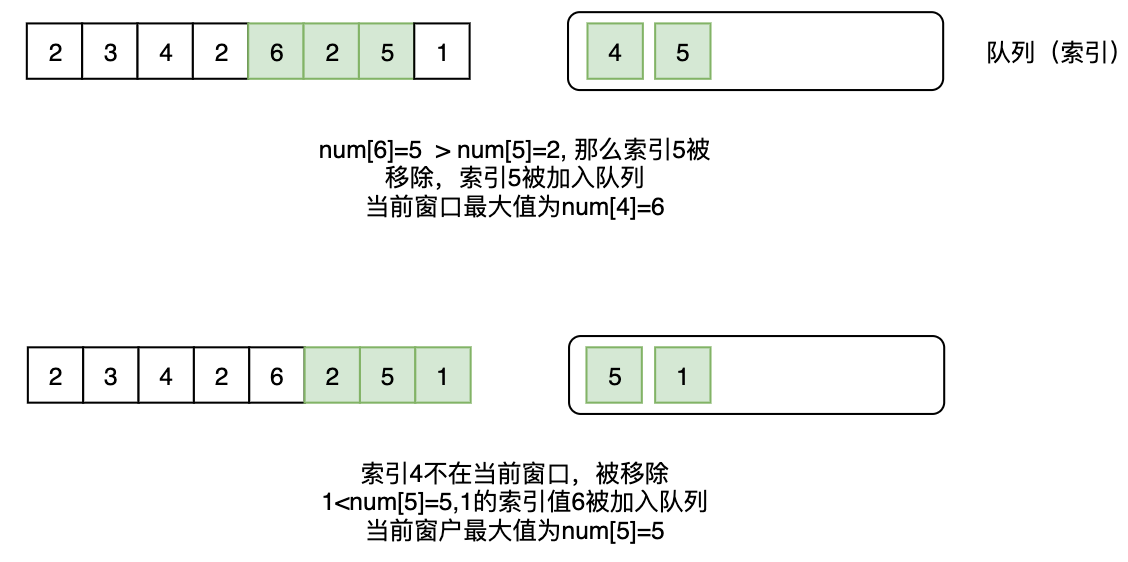
其次，使⽤⼀個雙向鏈表，⾥⾯保存的是索引，遍歷每⼀個元素，如果雙向隊列不為空且最後的元素作為索引的數值⼩於當前的元素，就把當前的元素的索引加到隊列的後⾯。（這樣可以保證隊列從頭到尾是單調遞減的，也就是隊尾的元素就是最⼩的元素）。

然後把當前的元素加進去隊列尾部。判斷隊列前⾯的元素是不是索引位置不符合，如果不符合，就移除隊列頭部的元素。

那麼此時的隊列⾸部肯定就是滑動窗⼝的最⼤值。（此處應該判斷滑動窗⼝⽣效的索引）

以 2, 3, 4, 2, 6, 2, 5, 1 為例：

所有的窗⼝最⼤值⾄此已經收集完成。

public class Solution64 {
     public static void main(String[] args) {
         int[] nums = {2, 3, 4, 2, 6, 2, 5, 1};
         System.out.println(new Solution64().maxInWindows(nums, 3));
     }
    
     public ArrayList<Integer> maxInWindows(int[] num, int size) {
         ArrayList<Integer> results = new ArrayList<>();
         if (num == null || num.length == 0 || num.length < size || size <= 0) {
         	return results;
         }
         
         LinkedList<Integer> integers = new LinkedList<>();
         for (int i = 0; i < num.length; i++) {
             while (!integers.isEmpty() && num[integers.peekLast()] < num[i]) {
             	integers.removeLast();
             }
             integers.addLast(i);
             while (i - integers.peekFirst() >= size) {
             	integers.removeFirst();
             }
             if (i >= size - 1) {
             	results.add(num[integers.peekFirst()]);
             }
         }
         return results;
     }
}

• 時間複雜度：O（n）,所有的元素都進⼊隊列，再出隊列
• 空間複雜度：O(n)，使⽤額外的隊列空間存儲索引以及窗⼝最⼤值。

動態規劃法（分塊思想）

將數組分成大小為k的塊，預處理每個位置的左右最大值

分塊思想：

• 將數組劃分為大小為k的塊（最後一塊可能不滿）
• left[i]：從當前塊開始到位置i的最大值
• right[i]：從位置i到當前塊結束的最大值

窗口最大值計算：

對於窗口[i, i+k-1]：

• 如果窗口完全在一個塊內：right[i]或left[i+k-1]就是最大值
• 如果窗口跨越兩個塊：最大值 = max(右塊的左最大值, 左塊的右最大值)

public class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums == null || nums.length == 0 || k <= 0) {
            return new int[0];
        }
        
        int n = nums.length;
        if (k == 1) return nums; // 窗口大小為1，直接返回原數組
        
        int[] left = new int[n];  // 從左到右的塊最大值
        int[] right = new int[n]; // 從右到左的塊最大值
        int[] result = new int[n - k + 1];
        
        // 構建left數組：從左到右的塊內最大值
        left[0] = nums[0];
        for (int i = 1; i < n; i++) {
            if (i % k == 0) {
                // 塊的首元素，重新開始計算
                left[i] = nums[i];
            } else {
                // 與前一個位置比較取最大值
                left[i] = Math.max(left[i - 1], nums[i]);
            }
        }
        
        // 構建right數組：從右到左的塊內最大值
        right[n - 1] = nums[n - 1];
        for (int i = n - 2; i >= 0; i--) {
            if ((i + 1) % k == 0) {
                // 塊的尾元素，重新開始計算
                right[i] = nums[i];
            } else {
                // 與後一個位置比較取最大值
                right[i] = Math.max(right[i + 1], nums[i]);
            }
        }
        
        // 計算每個窗口的最大值
        for (int i = 0; i <= n - k; i++) {
            // 窗口最大值 = max(右端點的左最大值, 左端點的右最大值)
            result[i] = Math.max(right[i], left[i + k - 1]);
        }
        
        return result;
    }
}

算法分析：

• 時間複雜度：O(n)，三次線性遍歷
• 空間複雜度：O(n)，需要兩個輔助數組