什麼是堆

堆是一種滿足以下條件的樹：

堆中的每一個節點值都大於等於（或小於等於）子樹中所有節點的值。或者説，任意一個節點的值都大於等於（或小於等於）所有子節點的值。

大家可以把堆(最大堆)理解為一個公司，這個公司很公平，誰能力強誰就當老大，不存在弱的人當老大，老大手底下的人一定不會比他強。這樣有助於理解後續堆的操作。

!!!特別提示：

• 很多博客説堆是完全二叉樹，其實並非如此，堆不一定是完全二叉樹，只是為了方便存儲和索引，我們通常用完全二叉樹的形式來表示堆，事實上，廣為人知的斐波那契堆和二項堆就不是完全二叉樹，它們甚至都不是二叉樹。
• （二叉）堆是一個數組，它可以被看成是一個 近似的完全二叉樹。——《算法導論》第三版

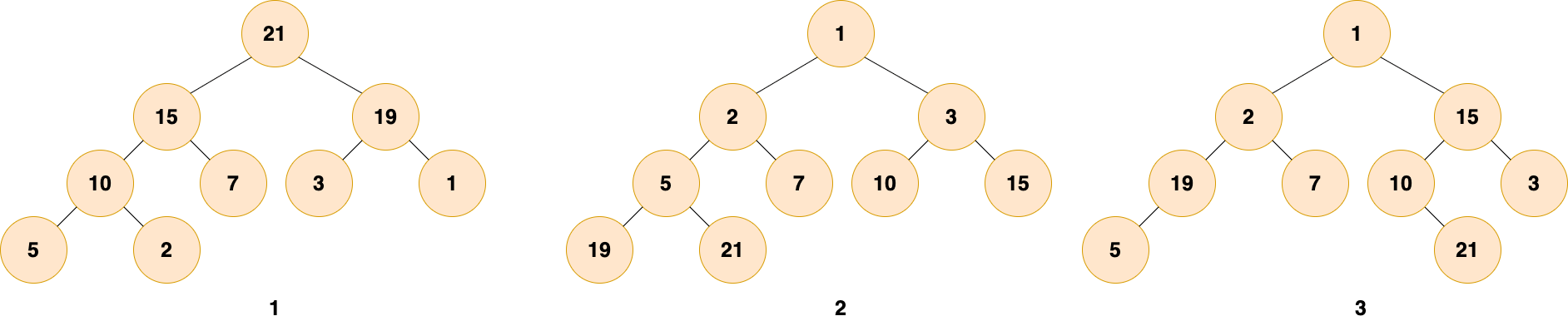
大家可以嘗試判斷下面給出的圖是否是堆？

第 1 個和第 2 個是堆。第 1 個是最大堆，每個節點都比子樹中所有節點大。第 2 個是最小堆，每個節點都比子樹中所有節點小。

第 3 個不是，第三個中，根結點 1 比 2 和 15 小，而 15 卻比 3 大，19 比 5 大，不滿足堆的性質。

堆的用途

當我們只關心所有數據中的最大值或者最小值，存在多次獲取最大值或者最小值，多次插入或刪除數據時，就可以使用堆。例如Top K問題

有小夥伴可能會想到用有序數組，初始化一個有序數組時間複雜度是 O(nlog(n))，查找最大值或者最小值時間複雜度都是 O(1)，但是，涉及到更新（插入或刪除）數據時，時間複雜度為 O(n)，即使是使用複雜度為 O(log(n)) 的二分法找到要插入或者刪除的數據，在移動數據時也需要 O(n) 的時間複雜度。

相對於有序數組而言，堆的主要優勢在於插入和刪除數據效率較高。 因為堆是基於完全二叉樹實現的，所以在插入和刪除數據時，只需要在二叉樹中上下移動節點，時間複雜度為 O(log(n))，相比有序數組的 O(n)，效率更高。

不過，需要注意的是：Heap 初始化的時間複雜度為 O(n)，而非O(nlogn)。

堆的分類

堆分為 最大堆 和 最小堆。二者的區別在於節點的排序方式。

• 最大堆：堆中的每一個節點的值都大於等於子樹中所有節點的值
• 最小堆：堆中的每一個節點的值都小於等於子樹中所有節點的值

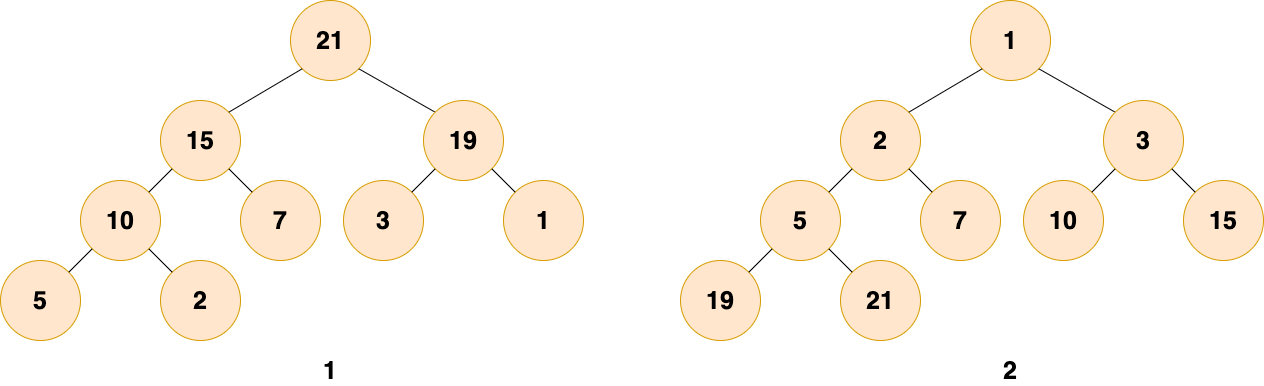
如下圖所示，圖 1 是最大堆，圖 2 是最小堆

堆的存儲

之前介紹樹的時候説過，由於完全二叉樹的優秀性質，利用數組存儲二叉樹即節省空間，又方便索引（若根結點的序號為 1，那麼對於樹中任意節點 i，其左子節點序號為 2*i，右子節點序號為 2*i+1）。

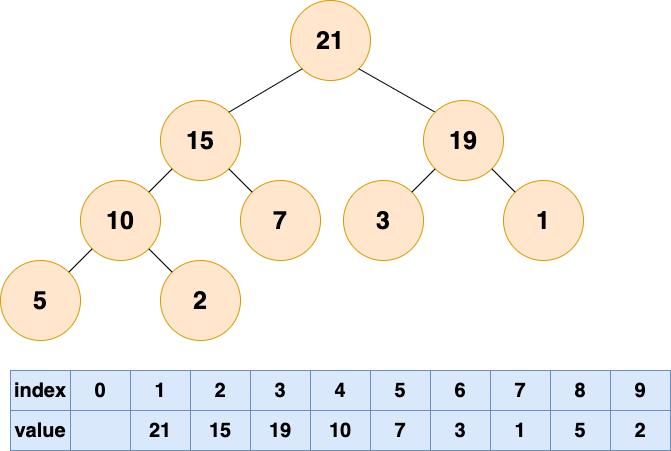
為了方便存儲和索引，（二叉）堆可以用完全二叉樹的形式進行存儲。存儲的方式如下圖所示：

堆的操作

堆的更新操作主要包括兩種 : 插入元素 和 刪除堆頂元素。操作過程需要着重掌握和理解。

在進入正題之前，再重申一遍，堆是一個公平的公司，有能力的人自然會走到與他能力所匹配的位置

插入元素

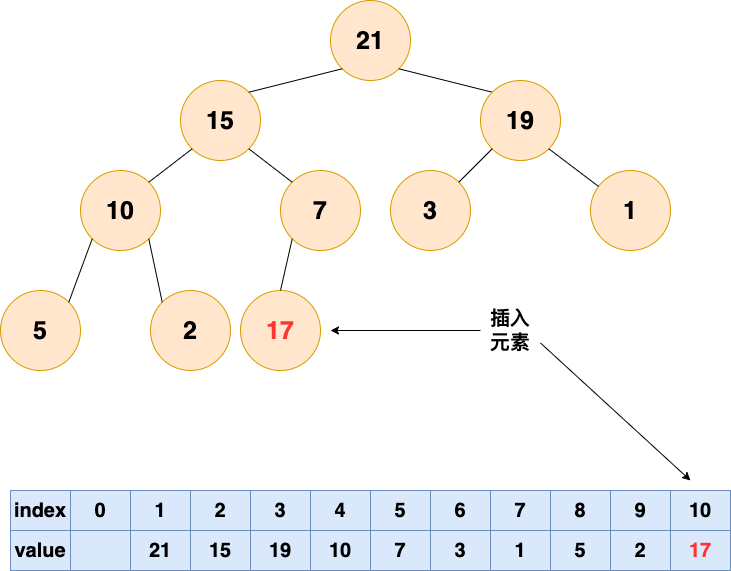
插入元素，作為一個新入職的員工，初來乍到，這個員工需要從基層做起

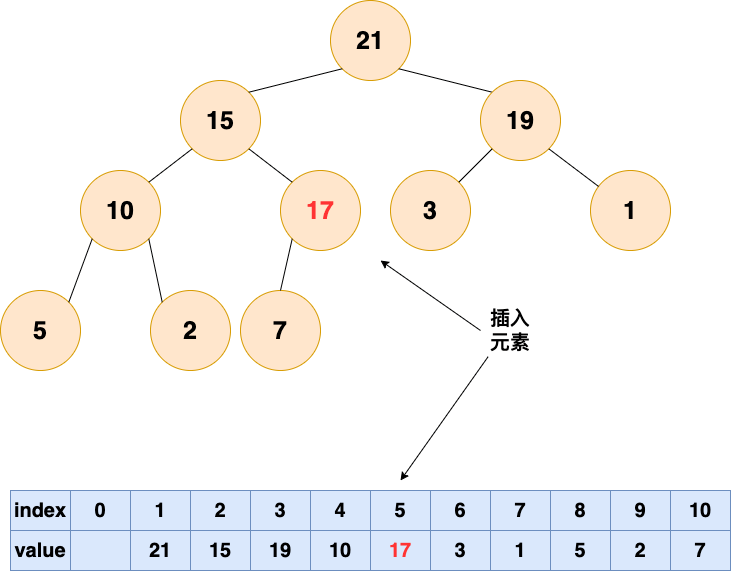
1.將要插入的元素放到最後

有能力的人會逐漸升職加薪，是金子總會發光的！！！

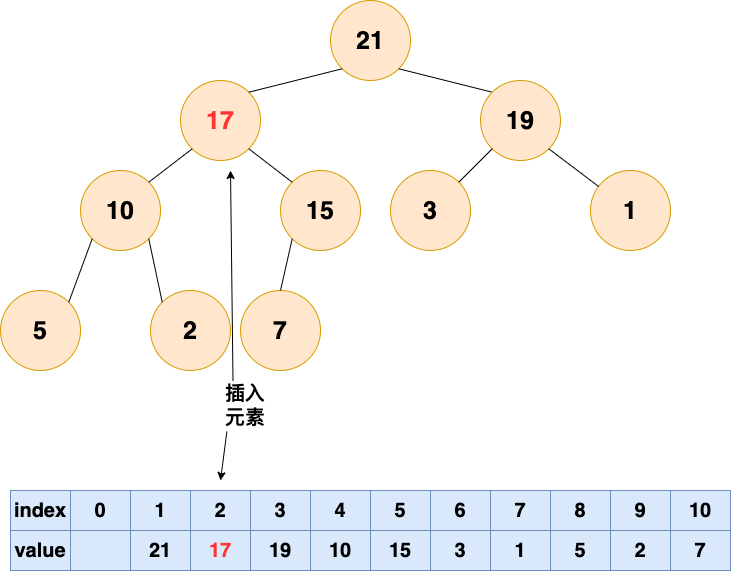
2.從底向上，如果父結點比該元素小，則該節點和父結點交換，直到無法交換

刪除堆頂元素

根據堆的性質可知，最大堆的堆頂元素為所有元素中最大的，最小堆的堆頂元素是所有元素中最小的。當我們需要多次查找最大元素或者最小元素的時候，可以利用堆來實現。

刪除堆頂元素後，為了保持堆的性質，需要對堆的結構進行調整，我們將這個過程稱之為"堆化"，堆化的方法分為兩種：

• 一種是自底向上的堆化，上述的插入元素所使用的就是自底向上的堆化，元素從最底部向上移動。
• 另一種是自頂向下堆化，元素由最頂部向下移動。在講解刪除堆頂元素的方法時，我將闡述這兩種操作的過程，大家可以體會一下二者的不同。

自底向上堆化

在堆這個公司中，會出現老大離職的現象，老大離職之後，他的位置就空出來了

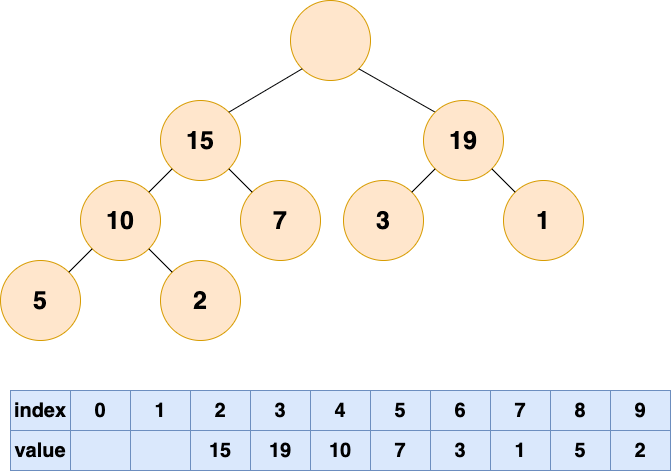
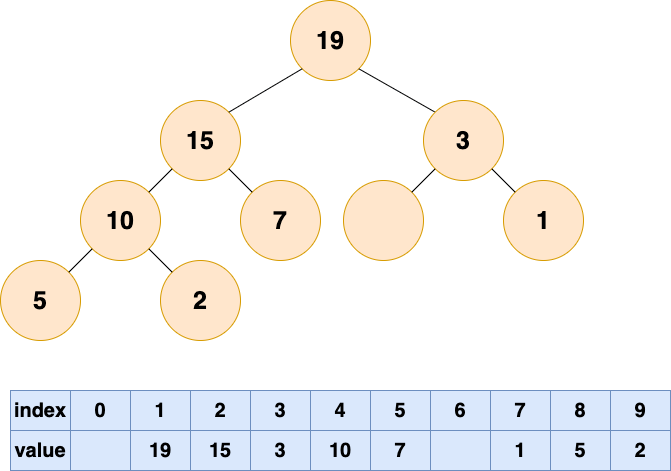
首先刪除堆頂元素，使得數組中下標為 1 的位置空出。

那麼他的位置由誰來接替呢，當然是他的直接下屬了，誰能力強就讓誰上唄

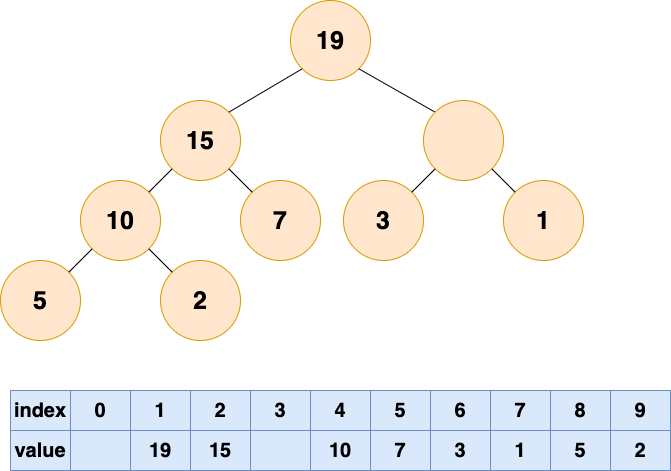
比較根結點的左子節點和右子節點，也就是下標為 2,3 的數組元素，將較大的元素填充到根結點(下標為 1)的位置。

這個時候又空出一個位置了，老規矩，誰有能力誰上

一直循環比較空出位置的左右子節點，並將較大者移至空位，直到堆的最底部

這個時候已經完成了自底向上的堆化，沒有元素可以填補空缺了，但是，我們可以看到數組中出現了“氣泡”，這會導致存儲空間的浪費。接下來我們試試自頂向下堆化。

自頂向下堆化

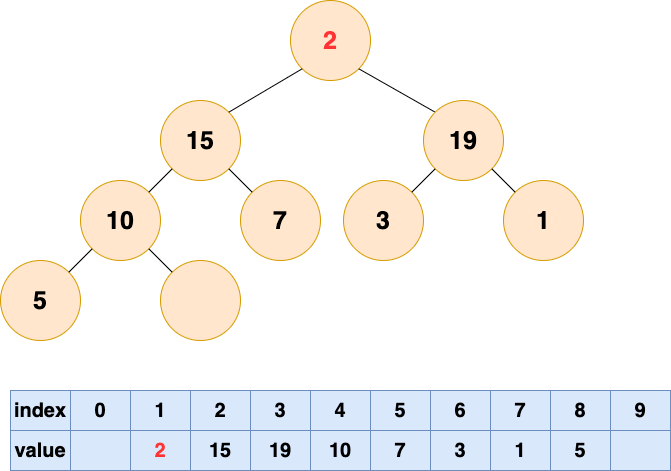
自頂向下的堆化用一個詞形容就是“石沉大海”，那麼第一件事情，就是把石頭抬起來，從海面扔下去。這個石頭就是堆的最後一個元素，我們將最後一個元素移動到堆頂。

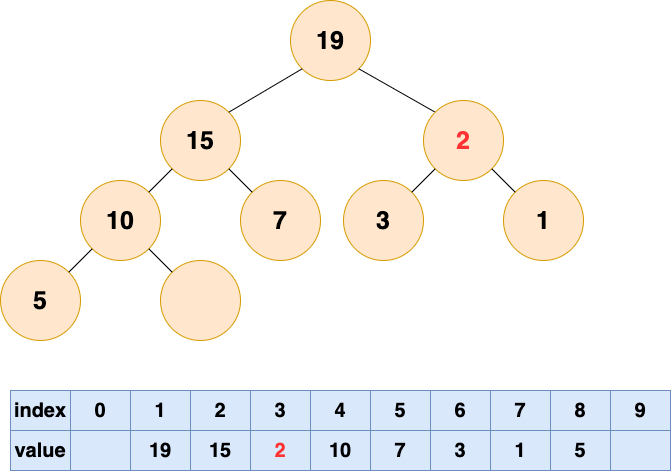
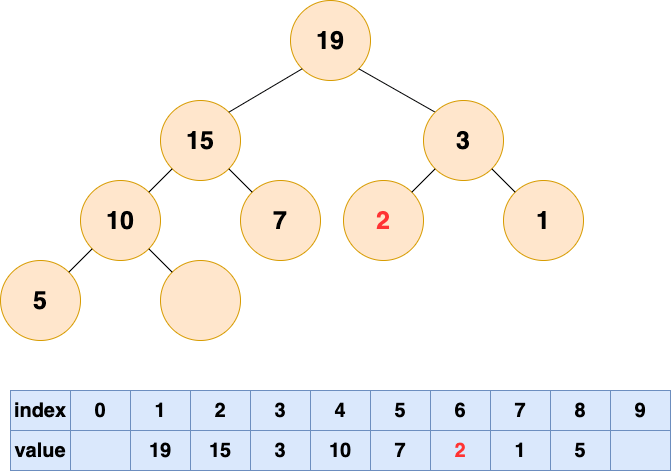
然後開始將這個石頭沉入海底，不停與左右子節點的值進行比較，和較大的子節點交換位置，直到無法交換位置。

堆的操作總結

• 插入元素：先將元素放至數組末尾，再自底向上堆化，將末尾元素上浮
• 刪除堆頂元素：刪除堆頂元素，將末尾元素放至堆頂，再自頂向下堆化，將堆頂元素下沉。也可以自底向上堆化，只是會產生“氣泡”，浪費存儲空間。最好採用自頂向下堆化的方式。

堆排序

堆排序的過程分為兩步：

• 第一步是建堆，將一個無序的數組建立為一個堆
• 第二步是排序，將堆頂元素取出，然後對剩下的元素進行堆化，反覆迭代，直到所有元素被取出為止。

建堆

如果你已經足夠了解堆化的過程，那麼建堆的過程掌握起來就比較容易了。建堆的過程就是一個對所有非葉節點的自頂向下堆化過程。

首先要了解哪些是非葉節點，最後一個節點的父結點及它之前的元素，都是非葉節點。也就是説，如果節點個數為 n，那麼我們需要對 n/2 到 1 的節點進行自頂向下（沉底）堆化。

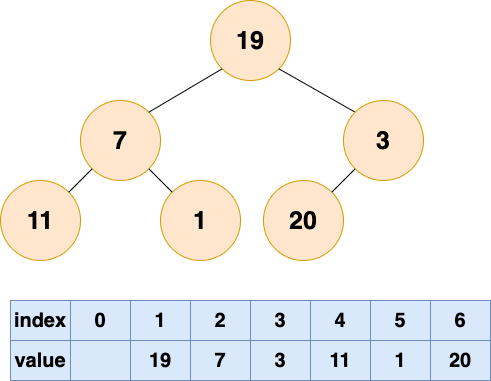
具體過程如下圖：

將初始的無序數組抽象為一棵樹，圖中的節點個數為 6，所以 4,5,6 節點為葉節點，1,2,3 節點為非葉節點，所以要對 1-3 號節點進行自頂向下（沉底）堆化，注意，順序是從後往前堆化，從 3 號節點開始，一直到 1 號節點。
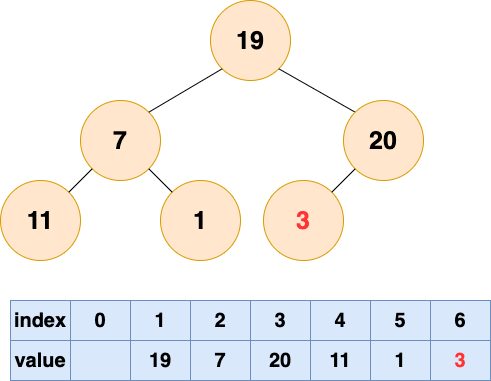
3 號節點堆化結果：

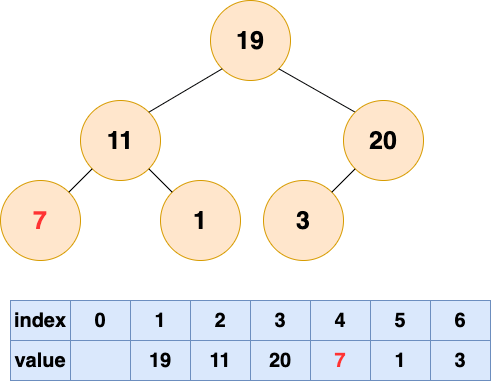
2 號節點堆化結果：

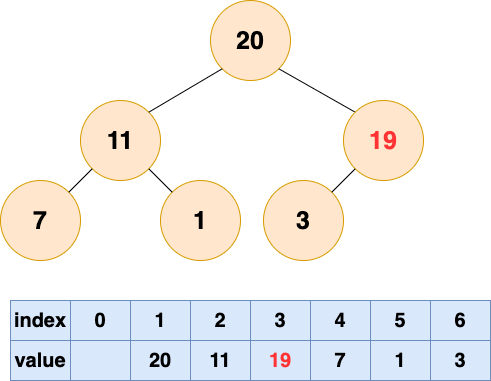
1 號節點堆化結果：

至此，數組所對應的樹已經成為了一個最大堆，建堆完成！

排序

由於堆頂元素是所有元素中最大的，所以我們重複取出堆頂元素，將這個最大的堆頂元素放至數組末尾，並對剩下的元素進行堆化即可。

現在思考兩個問題：

• 刪除堆頂元素後需要執行自頂向下（沉底）堆化還是自底向上（上浮）堆化？
• 取出的堆頂元素存在哪，新建一個數組存？

先回答第一個問題，我們需要執行自頂向下（沉底）堆化，這個堆化一開始要將末尾元素移動至堆頂，這個時候末尾的位置就空出來了，由於堆中元素已經減小，這個位置不會再被使用，所以我們可以將取出的元素放在末尾。

機智的小夥伴已經發現了，這其實是做了一次交換操作，將堆頂和末尾元素調換位置，從而將取出堆頂元素和堆化的第一步(將末尾元素放至根結點位置)進行合併。

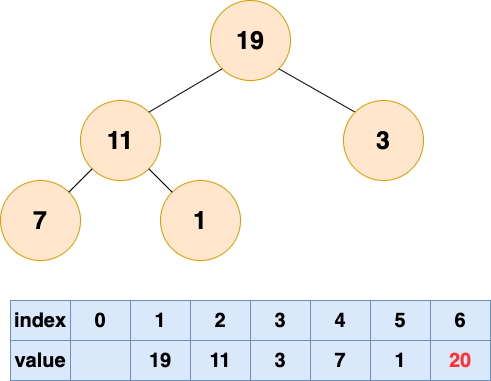
詳細過程如下圖所示：

取出第一個元素並堆化：

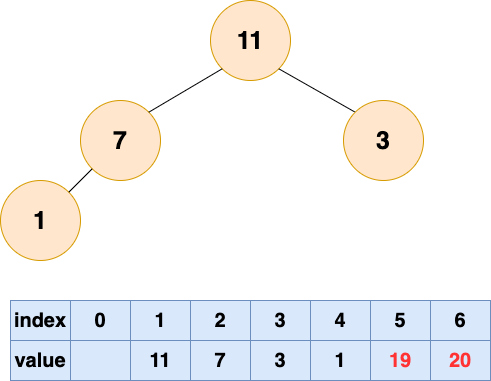
取出第二個元素並堆化：

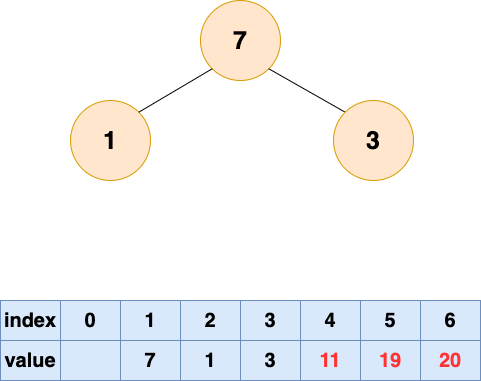
取出第三個元素並堆化：

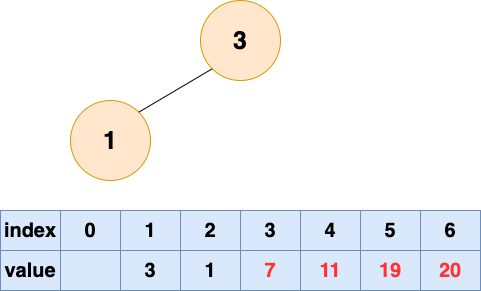
取出第四個元素並堆化：

取出第五個元素並堆化：

取出第六個元素並堆化：

堆排序完成！