題⽬描述

輸⼊⼀個⻓度為n 的整型數組array ，數組中的⼀個或連續多個整數組成⼀個⼦數組，找到⼀個具有
最⼤和的連續⼦數組。

1. ⼦數組是連續的，⽐如[1,3,5,7,9] 的⼦數組有[1,3] ， [3,5,7] 等等，但是[1,3,7] 不是⼦數組
2. 如果存在多個最⼤和的連續⼦數組，那麼返回其中⻓度最⻓的，該題數據保證這個最⻓的只存在⼀個
3. 該題定義的⼦數組的最⼩⻓度為1 ，不存在為空的⼦數組，即不存在[]是某個數組的⼦數組
4. 返回的數組不計⼊空間複雜度計算

示例 1
輸⼊：[1,-2,3,10,-4,7,2,-5]
返回值：[3,10,-4,7,2]
説明：經分析可知，輸⼊數組的⼦數組[3,10,-4,7,2]可以求得最⼤和為18，故返回[3,10,-4,7,2]

示例 2
輸⼊：[1]
返回值：[1]

思路及解答

暴力枚舉

通過三重循環枚舉所有可能的子數組，使用三重循環枚舉所有可能的子數組起始和結束位置，計算每個子數組的和

public class Solution {
    public int[] findMaxSubarray(int[] array) {
        if (array == null || array.length == 0) {
            return new int[0];
        }
        
        int n = array.length;
        int maxSum = Integer.MIN_VALUE;
        int start = 0, end = 0;
        
        // 第一重循環：子數組起始位置
        for (int i = 0; i < n; i++) {
            // 第二重循環：子數組結束位置
            for (int j = i; j < n; j++) {
                int currentSum = 0;
                // 第三重循環：計算子數組和
                for (int k = i; k <= j; k++) {
                    currentSum += array[k];
                }
                
                // 更新最大和及位置（優先選擇長度更長的）
                if (currentSum > maxSum || (currentSum == maxSum && (j - i) > (end - start))) {
                    maxSum = currentSum;
                    start = i;
                    end = j;
                }
            }
        }
        
        // 構建結果數組
        int[] result = new int[end - start + 1];
        System.arraycopy(array, start, result, 0, result.length);
        return result;
    }
}

• 時間複雜度：O(n³)，三重循環嵌套
• 空間複雜度：O(1)，除結果外只使用常數空間

優化枚舉法（前綴和思想）

在暴力法基礎上優化，利用前綴和在計算子數組和時複用之前的結果，減少一層循環

public class Solution {
    public int[] findMaxSubarray(int[] array) {
        if (array == null || array.length == 0) {
            return new int[0];
        }
        
        int n = array.length;
        int maxSum = Integer.MIN_VALUE;
        int start = 0, end = 0;
        
        // 外層循環：子數組起始位置
        for (int i = 0; i < n; i++) {
            int currentSum = 0;
            // 內層循環：從起始位置向後累加
            for (int j = i; j < n; j++) {
                currentSum += array[j]; // 複用之前計算的結果
                
                // 更新最大和（優先選擇長度更長的）
                if (currentSum > maxSum || (currentSum == maxSum && (j - i) > (end - start))) {
                    maxSum = currentSum;
                    start = i;
                    end = j;
                }
            }
        }
        
        return buildResult(array, start, end);
    }
    
    private int[] buildResult(int[] array, int start, int end) {
        int[] result = new int[end - start + 1];
        System.arraycopy(array, start, result, 0, result.length);
        return result;
    }
}

• 時間複雜度：O(n²)，減少了一層循環
• 空間複雜度：O(1)，常數級別空間複雜度

分治法（遞歸思維）

採用分治思想，將問題分解為更小的子問題

將問題分解為左半部分、右半部分和跨越中間的三部分

即遞歸求解左右子數組，合併時處理跨越中間的情況

public class Solution {
    public int[] findMaxSubarray(int[] array) {
        if (array == null || array.length == 0) {
            return new int[0];
        }
        Result result = findMaxSubarrayHelper(array, 0, array.length - 1);
        return buildResult(array, result.start, result.end);
    }
    
    private Result findMaxSubarrayHelper(int[] array, int left, int right) {
        // 基準情況：單個元素
        if (left == right) {
            return new Result(left, right, array[left]);
        }
        
        int mid = left + (right - left) / 2;
        
        // 遞歸求解左右兩部分
        Result leftResult = findMaxSubarrayHelper(array, left, mid);
        Result rightResult = findMaxSubarrayHelper(array, mid + 1, right);
        Result crossResult = findMaxCrossingSubarray(array, left, mid, right);
        
        // 返回三者中的最大值（長度優先）
        return getMaxResult(leftResult, rightResult, crossResult);
    }
    
    private Result findMaxCrossingSubarray(int[] array, int left, int mid, int right) {
        // 向左擴展找最大和
        int leftSum = Integer.MIN_VALUE;
        int sum = 0;
        int maxLeft = mid;
        for (int i = mid; i >= left; i--) {
            sum += array[i];
            if (sum > leftSum) {
                leftSum = sum;
                maxLeft = i;
            }
        }
        
        // 向右擴展找最大和
        int rightSum = Integer.MIN_VALUE;
        sum = 0;
        int maxRight = mid + 1;
        for (int i = mid + 1; i <= right; i++) {
            sum += array[i];
            if (sum > rightSum) {
                rightSum = sum;
                maxRight = i;
            }
        }
        
        return new Result(maxLeft, maxRight, leftSum + rightSum);
    }
    
    private Result getMaxResult(Result r1, Result r2, Result r3) {
        Result maxResult = r1;
        if (r2.sum > maxResult.sum || (r2.sum == maxResult.sum && (r2.end - r2.start) > (maxResult.end - maxResult.start))) {
            maxResult = r2;
        }
        if (r3.sum > maxResult.sum || (r3.sum == maxResult.sum && (r3.end - r3.start) > (maxResult.end - maxResult.start))) {
            maxResult = r3;
        }
        return maxResult;
    }
    
    private int[] buildResult(int[] array, int start, int end) {
        int[] result = new int[end - start + 1];
        System.arraycopy(array, start, result, 0, result.length);
        return result;
    }
    
    // 輔助類存儲子數組結果
    class Result {
        int start, end, sum;
        Result(int s, int e, int sum) {
            this.start = s;
            this.end = e;
            this.sum = sum;
        }
    }
}

• 時間複雜度：O(n log n)，遞歸深度為log n，每層處理時間為O(n)
• 空間複雜度：O(log n)，遞歸調用棧的深度

動態規劃-Kadane算法（最優解）

遍歷數組，維護當前子數組和，根據規則重置或擴展當前子數組

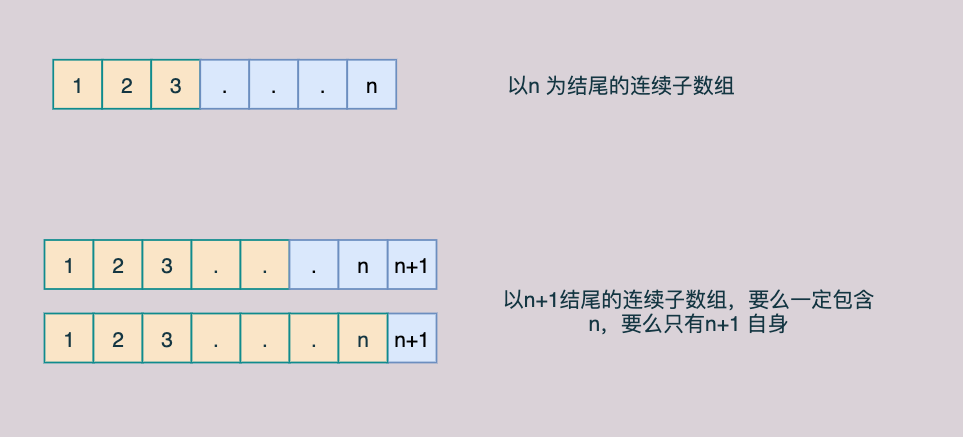
假設現在有 n 個元素，突然加上⼀個元素，變成 n+1 個元素，對連續⼦數組的最⼤和有什麼影響呢？

我們只需要知道以每⼀個元素結尾的最⼤連續⼦數組，再維護⼀個最⼤的值即可。

假設數組為num[] ，⽤ dp[i] 表示以下標 i 為終點的最⼤連續⼦數組和，遍歷每⼀個新的元素nums[i+1] ，以 num[i+1] 為連續⼦數組的情況只有兩種：

• dp[i] + num[i+1]
• 只有num[i+1]

所以以nums[n] 結尾的最⼤連續⼦數組和為： dp[i] = max( dp[i-1] + num[i], num[i])

在計算的過程中，需要維護⼀個最⼤的值，並且把該連續⼦數組的左邊界以及右邊界維護好，最後根據維護的區間返回。

public class Solution85 {
    public int[] FindGreatestSumOfSubArray(int[] array) {
        int[] dp = new int[array.length];
        dp[0] = array[0];
        int maxsum = dp[0];
        int left = 0, right = 0;
        int maxLeft = 0, maxRight = 0;
        for (int i = 1; i < array.length; i++) {
            right++;
            dp[i] = Math.max(dp[i - 1] + array[i], array[i]);
            if (dp[i - 1] + array[i] < array[i]) {
                left = right;
            }
            // 更新最⼤值以及更新最⼤和的⼦數組的邊界
            if (dp[i] > maxsum || dp[i] == maxsum && (right - left + 1) > (maxRight - maxLeft + 1)) {
                maxsum = dp[i];
                maxLeft = left;
                maxRight = right;
            }
        }
        // 保存結果
        int[] res = new int[maxRight - maxLeft + 1];
        for (int i = maxLeft, j = 0; i <= maxRight; i++, j++) {
            res[j] = array[i];
        }
        return res;
    }
}

• 時間複雜度：O(n)，單次遍歷數組
• 空間複雜度：O(1)，只使用常數變量