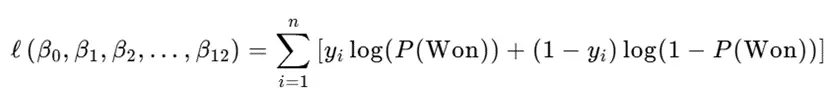全文鏈接：https://tecdat.cn/?p=44748
原文出處：拓端數據部落公眾號

關於分析師

在此對Xinpeng Wang對本文所作的貢獻表示誠摯感謝，他在浙江財經大學完成了應用統計學專業的學士學位，專注老年教育調查數據分析、奧運獎牌預測模型建立領域。擅長R語言、Python、數據預處理、統計分析、統計建模。曾參與老年教育調查數據的清洗與分析工作，主導完成奧運獎牌預測模型的搭建與驗證，憑藉紮實的統計理論基礎和編程實踐能力，為相關分析工作提供了精準的技術支撐。

專題名稱：奧運獎牌預測的多模型融合分析與因果關聯挖掘

引言

從1896年現代奧運會誕生至今，獎牌榜始終是衡量各國體育競技實力的核心標尺，其不僅承載着國民的體育榮譽感，更成為各國奧委會制定資源配置、項目佈局策略的重要依據。隨着全球體育競爭的日趨激烈，傳統依靠經驗判斷的獎牌預測方式已難以滿足精準決策的需求，如何通過數據建模的方式量化各類影響因素、挖掘獎牌數背後的潛在規律，成為體育數據分析領域的核心研究方向。
本文聚焦2028年洛杉磯夏季奧運會獎牌預測這一實際業務場景，整合多屆奧運會的獎牌數、運動員人數、項目參與情況、東道主信息等核心數據，構建了多模型融合的分析框架——既實現了各國金牌數、總獎牌數的精準預測，也完成了未獲獎國家首獎概率的估算，同時揭示了奧運項目設置與獎牌數量之間的深層因果關係。

本文內容改編自過往客户諮詢項目的技術沉澱並且已通過實際業務校驗，該項目完整代碼與數據已分享至交流社羣。閲讀原文進羣，可與800+行業人士交流成長；還提供人工答疑，拆解核心原理、代碼邏輯與業務適配思路，幫大家既懂 怎麼做，也懂 為什麼這麼做；遇代碼運行問題，更能享24小時調試支持。
本研究的創新點在於突破了傳統相關性分析的侷限，採用Liang-Kleeman信息流方法量化項目設置對獎牌數的因果影響，同時結合CNN神經網絡、Logistic迴歸、多元線性迴歸及隨機森林模型，形成“數值預測-概率估算-因果挖掘”三位一體的分析體系。下文將從數據預處理、模型構建、結果分析三個維度展開，結合實操代碼與可視化結果，讓讀者清晰掌握完整的分析流程與核心技術要點。

研究脈絡流程圖（豎版）

<pre data-index="0" name="code" style="color: rgb(0, 0, 0); font-size: 14px; font-style: normal; font-variant-ligatures: normal; font-variant-caps: normal; font-weight: 400; letter-spacing: normal; orphans: 2; text-align: left; text-indent: 0px; text-transform: none; widows: 2; word-spacing: 0px; -webkit-text-stroke-width: 0px; background-color: rgb(255, 255, 255); text-decoration-thickness: initial; text-decoration-style: initial; text-decoration-color: initial;"><img alt="" src="https://i-blog.csdnimg.cn/direct/eb428fc1e4264c909df92fbf78e3e0a2.png" style="border: 0px; max-width: 650px;">
</pre>

項目文件目錄結構

數據預處理與模型選擇基礎

數據來源與核心處理邏輯

本研究數據集涵蓋1896-2024年曆屆夏季奧運會的運動員信息、獎牌獲得情況、東道主標識等核心內容。數據處理需解決兩大核心問題：一是團體賽獎牌計數冗餘問題（團體賽中每位隊員均記獎導致與官方計數不一致），二是數據格式適配不同模型輸入要求的問題。
具體處理步驟如下：

1. 按年份、國家（NOC）、運動項目分類，統計各國各項目參賽人數、金銀銅牌獲得者人數、男女運動員數量及比例，並結合東道主數據標註當年各國是否為東道主；
2. 整合2004-2024年數據構建基礎數據集，依據2028年奧運會確定的比賽項目清單，篩選出有效數據；
3. 剔除1906年等異常年份數據，完成缺失值、異常值校驗，確保數據質量。

初始模型嘗試與優化方向

研究初期首先構建了多元線性迴歸模型分別用於金牌數（Gold模型）和總獎牌數（Total模型）預測，但模型擬合效果不佳——Gold模型的R²僅為0.469213，Total模型的R²僅為0.451534，表明線性模型難以捕捉變量間的複雜非線性關係。


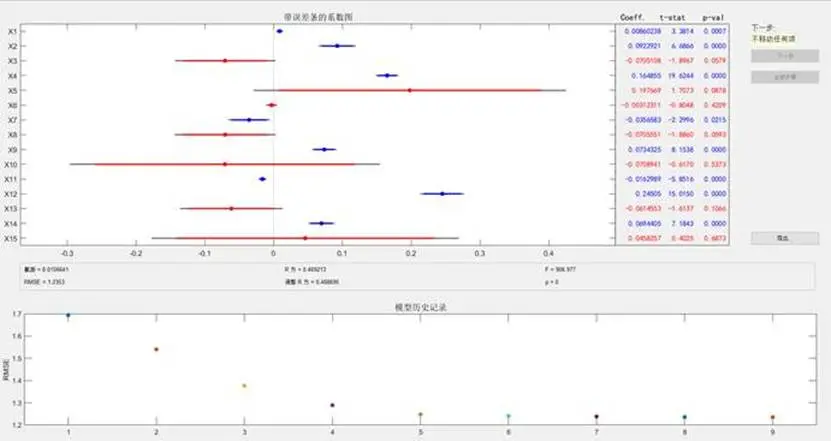
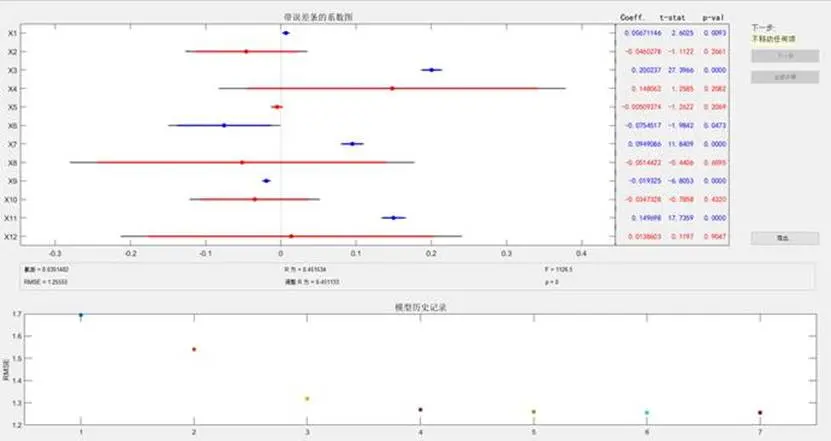
基於此，研究決定更換模型架構，選用卷積神經網絡（CNN）重構獎牌預測模型——CNN具備強大的特徵提取能力，且參數量相對可控，更適配本研究的大規模數據集分析場景，同時引入隨機森林模型作為對比驗證，提升結果可靠性。

相關文章

TCN時序卷積網絡、CNN、RNN、LSTM、GRU神經網絡工業設備運行監測、航空客運量時間數據集預測可視化|附代碼數據

原文鏈接：https://tecdat.cn/?p=43941

核心模型構建與代碼實操

CNN神經網絡實現獎牌數精準預測

模型背景與架構設計

卷積神經網絡（CNN）憑藉局部連接、權值共享的特性，能夠高效提取高維數據中的隱藏特徵，是處理結構化數據預測任務的優選模型。本研究構建的CNN模型以前三屆奧運會的核心特徵（獎牌數、參賽人數、男女比例、東道主標識等12維特徵）為輸入，經卷積層、激活層、池化層完成特徵提取與降維，最終通過全連接層輸出獎牌數預測值。

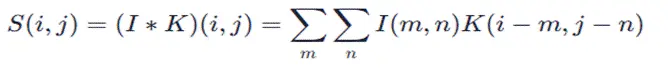
模型的核心架構設計如下：

• 輸入層：接收12維預處理後的特徵數據；
• 卷積層：設置2層卷積，分別生成16張、32張特徵圖，捕捉特徵間的關聯；
• 激活層：採用ReLU函數增強模型非線性擬合能力；
• 池化層：通過最大池化降低特徵維度，減少計算量；
• Dropout層：設置0.1的丟棄率，防止模型過擬合；
• 全連接層+迴歸層：輸出最終的獎牌數預測值。

關鍵代碼（MATLAB，變量名與語法優化）

% 清空環境變量，避免干擾warning off; close all; clear; clc;% 導入數據並隨機劃分訓練集（66.7%）和測試集（33.3%）medal_data = xlsread("Total.xlsx");random_idx = randperm(size(medal_data, 1)); % 隨機打亂數據索引train_feature = medal_data(random_idx(1:5478), 1:12)'; % 訓練集特徵train_target = medal_data(random_idx(1:5478), 13)'; % 訓練集目標值（獎牌數）test_feature = medal_data(random_idx(5479:end), 1:12)'; % 測試集特徵test_target = medal_data(random_idx(5479:end), 13)'; % 測試集目標值% 數據歸一化（映射至0-1區間，消除量綱影響）[train_feat_norm, norm_param_input] = mapminmax(train_feature, 0, 1);test_feat_norm = mapminmax('apply', test_feature, norm_param_input);[train_tar_norm, norm_param_output] = mapminmax(train_target, 0, 1);test_tar_norm = mapminmax('apply', test_target, norm_param_output);% 數據重塑為四維張量，適配CNN輸入格式

模型評估與結果可視化

模型評估結果顯示：訓練集R²為0.51512、MAE為0.35293、MBE為-0.00010978；測試集R²為0.29542、MAE為0.37414、MBE為0.0025216。MBE接近0表明模型無系統性偏差，MAE處於可接受範圍，説明模型具備實際應用價值。


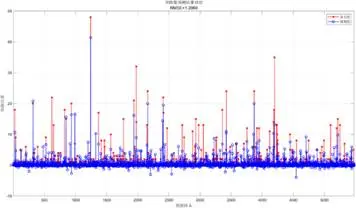
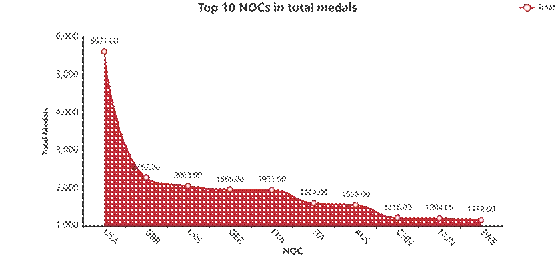
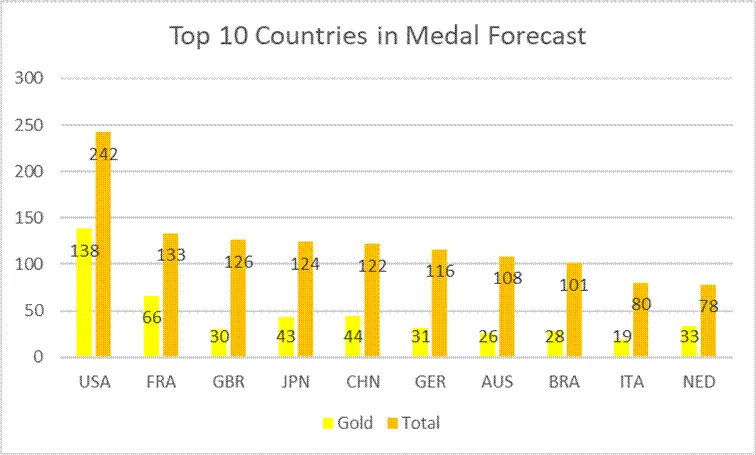
從可視化結果可見，預測值與真實值在低數值區間貼合度較高，模型能夠有效捕捉獎牌數的核心變化趨勢。2028年奧運會獎牌預測結果顯示，獎牌分佈呈現顯著的冪律特徵——體育強國與其他國家差距明顯，美國仍將保持絕對領先優勢，中日等國競爭趨於激烈。

Logistic迴歸估算未獲獎國家首獎概率

模型核心邏輯

針對76個從未獲得奧運獎牌的國家，本研究將“是否獲獎”定義為二分類變量（獲獎=1，未獲獎=0），選取前三屆參賽人數、項目數、東道主身份等為特徵，構建Logistic迴歸模型量化2028年首獎概率。模型核心公式為：

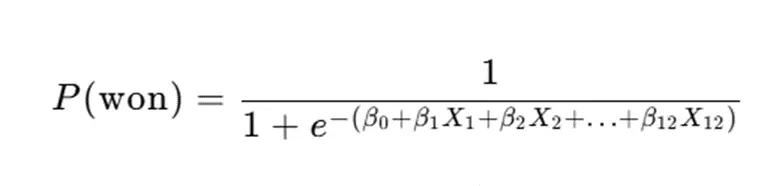
其中，P(won)為獲獎概率，β₀-β₁₂為迴歸係數，X為特徵變量，模型通過最大化似然函數求解最優係數：


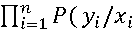
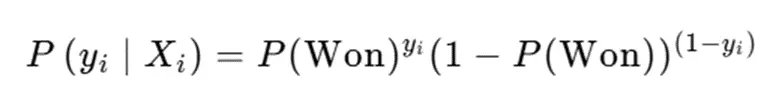
為簡化計算並提升數值穩定性，對似然函數取對數得到對數似然函數：

關鍵代碼（MATLAB，優化後）

% 導入數據並預處理logist_data = xlsread("logist.xlsx");feature_data = logist_data(:, 1:18); % 提取18維特徵變量label_data = logist_data(:, 21); % 提取二分類標籤（0/1）[feat_num, feat_dim] = size(feature_data);feature_data = [feature_data, ones(feat_num, 1)]; % 添加截距項% 梯度下降求解迴歸係數（省略迭代收斂判斷代碼）beta_coef = zeros(feat_dim + 1, 1);iter_times = 1500; % 迭代次數learn_rate = 0.01; % 學習率for iter = 1:iter_times z_value = feature_data * beta_coef; h_value = 1 ./ (1 + exp(-z_value)); % Sigmoid激活函數 error_val = h_value - label_data; grad_val = feature_data' * error_val; beta_coef = beta_coef - learn_rate / feat_num * grad_val; ... % 省略收斂判斷代碼end

預測結果分析

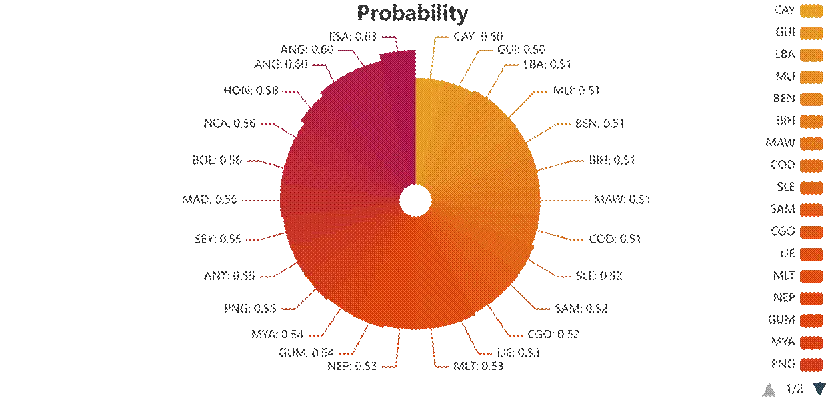
模型設定0.5為概率閾值，預測76個未獲獎國家中有26個可能在2028年實現首獎突破，但所有國家的獲獎概率均低於0.7，其中薩爾瓦多（ESA）的概率最高（0.63），反映出新興國家實現奧運獎牌突破仍面臨較大挑戰。

Liang-Kleeman信息流分析項目設置與獎牌數的因果關係

核心理論

傳統相關性分析僅能反映變量間的關聯程度，無法明確因果方向，而Liang-Kleeman信息流方法可量化變量間的因果影響強度與方向，核心公式為：

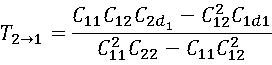
其中，T₂→₁為從X₂到X₁的信息流值，Cᵢⱼ為協方差，Cᵢ.dⱼ為經前差處理後的協方差；若T₂→₁≠0且通過顯著性檢驗，則X₂是X₁的因。

關鍵代碼（MATLAB，優化後）

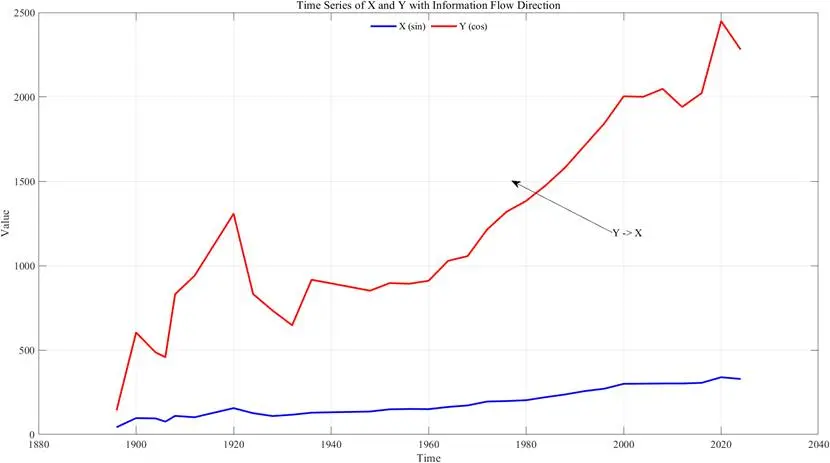
% 繪製標記因果方向的時間序列圖figure;plot(year_series, event_count, 'b', 'LineWidth', 2);hold on;plot(year_series, medal_count, 'r', 'LineWidth', 2);% 根據信息流方向添加箭頭標註if T_event_to_medal > 0 annotation('textarrow', [0.6 0.7], [0.6 0.5], 'String', '項目設置數→獎牌數');endxlabel('年份');ylabel('數量');legend('項目設置數', '獎牌總數');title('項目設置與獎牌數的因果方向標記');grid on;hold off;% 自定義信息流計算函數function T_val = calc_liang_kleeman(X_series, Y_series, t_series) if length(X_series) ~= length(Y_series) error('兩個時間序列長度必須一致'); end % 有限差分計算時間導數（省略邊界值處理代碼） dX_dt = diff(X_series) ./ diff(t_series); dY_dt = diff(Y_series) ./ diff(t_series); X_series = X_series(1:end-1); Y_series = Y_series(1:end-1); ... % 省略協方差、方差計算細節代碼 % 計算信息流值 T_val = (1 / var(Y_series)) * cov(X_series, dY_dt) - ... (cov(X_series,Y_series)/(var(X_series)*var(Y_series))) * cov(X_series, dX_dt);end

分析結果

信息流計算結果顯示T≠0且通過顯著性檢驗，表明奧運項目設置數量的增加是獎牌總數增長的重要原因——更多的項目設置能提供更多奪牌機會，也能吸引更多運動員參與，這也為東道主通過優化項目設置提升獎牌數提供了理論依據。

研究結論與服務支持

核心結論

1. 獎牌預測層面：CNN模型能夠有效捕捉奧運獎牌數的變化規律，2028年奧運會獎牌分佈仍呈冪律特徵，美國保持領先優勢，中日等國競爭激烈，部分國家需強化項目發展均衡性；
2. 首獎概率層面：26個未獲獎國傢俱備首獎潛力，但整體概率偏低，相關國家可針對性投入資源培育優勢項目；
3. 因果關係層面：項目設置數量與獎牌總數存在顯著的因果關聯，東道主可通過增設優勢項目提升獎牌競爭力。