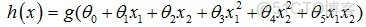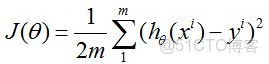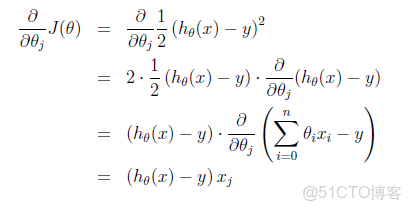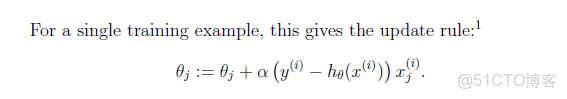斯坦福大學公開課 ：機器學習課程 [第2集] 監督學習應用.梯度下降

http://v.163.com/movie/2008/1/B/O/M6SGF6VB4_M6SGHJ9BO.html

Matlab實現線性迴歸和邏輯迴歸: Linear Regression & Logistic Regression

octave入門教程

關於非線性優化fminbnd函數的説明（僅供新手參考）（也可作為fmincon函數的參考）

http://www.docin.com/p-214776767.html

由於是剛開始接觸ML和MATLAB，所以記錄一些比較簡單的筆記。


個人實驗中未使用MATLAB，而是使用了Octave作為替代，區別只是把函數結束的end改成endfunction即可，其他部分和matlab保持一致。

文中主要框架內容參考 



第一部分：基本模型


在解決擬合問題的解決之前，我們首先回憶一下線性迴歸基本模型。

設待擬合參數 θn*1 和輸入參數[ xm*n, ym*1 ] 。

對於各類擬合我們都要根據梯度下降的算法，給出兩部分：

①   cost function（指出真實值y與擬合值h<hypothesis>之間的距離）：給出cost function 的表達式，每次迭代保證cost function的量減小；給出梯度gradient，即cost function對每一個參數θ的求導結果。

function

 

②   Gradient_descent（主函數）：用來運行梯度下降算法，調用上面的cost function進行不斷迭代，直到最大迭代次數達到給定標準或者cost function返回值不再減小。

function

 

線性迴歸：擬合方程為hθ(x)=θ0x0+θ1x1+…+θnxn，當然也可以有xn的冪次方作為線性迴歸項（如

bp算法matlab線性迴歸結果分析_線性迴歸

），這與普通意義上的線性不同，而是類似多項式的概念。其cost function 為：

bp算法matlab線性迴歸結果分析_bp算法matlab線性迴歸結果分析_02

第二部分：Y=θ0+θ1X1型---線性迴歸（直線擬合）


在Matlab 線性擬合 & 非線性擬閤中我們已經講過如何用matlab自帶函數fit進行直線和曲線的擬合，非常實用。而這裏我們是進行ML課程的學習，因此研究如何利用前面講到的梯度下降法（gradient descent）進行擬合。


cost function：

[cpp]  view plain copy

1. function [ jVal,gradient ] = costFunction2( theta )  
2. %COSTFUNCTION2 Summary of this function goes here  
3. %   linear regression -> y=theta0 + theta1*x  
4. %   parameter: x:m*n  theta:n*1   y:m*1   (m=4,n=1)  
5. %     
6.   
7. %Data  
8. x=[1;2;3;4];  
9. y=[1.1;2.2;2.7;3.8];  
10. m=size(x,1);  
11.   
12. hypothesis = h_func(x,theta);  
13. delta = hypothesis - y;  
14. jVal=sum(delta.^2);  
15.   
16. gradient(1)=sum(delta)/m;  
17. gradient(2)=sum(delta.*x)/m;  
18.   
19. end


其中，h_func是hypothesis的結果：

[cpp]  view plain copy

1. function [res] = h_func(inputx,theta)  
2. %H_FUNC Summary of this function goes here  
3. %   Detailed explanation goes here  
4.   
5.   
6. %cost function 2  
7. res= theta(1)+theta(2)*inputx;  
8. end


Gradient_descent：

[cpp]  view plain copy

1. function [optTheta,functionVal,exitFlag]=Gradient_descent( )  
2. %GRADIENT_DESCENT Summary of this function goes here  
3. %   Detailed explanation goes here  
4.   
5. 'GradObj','on','MaxIter',100);  
6.   initialTheta = zeros(2,1);  
7.   [optTheta,functionVal,exitFlag] = fminunc(@costFunction2,initialTheta,options);  
8.   
9. end

result：

[cpp]  view plain copy

1. >> [optTheta,functionVal,exitFlag] = Gradient_descent()  
2.   
3. Local minimum found.  
4.   
5. Optimization completed because the size of the gradient is less than  
6. the default value of the function tolerance.  
7.   
8. <stopping criteria details>  
9.   
10.   
11. optTheta =  
12.   
13.     0.3000  
14.     0.8600  
15.   
16.   
17. functionVal =  
18.   
19.     0.0720  
20.   
21.   
22. exitFlag =  
23.   
24.      1



驗證：

[cpp]  view plain copy

1. function [ parameter ] = checkcostfunc(  )  
2. %CHECKC2 Summary of this function goes here  
3. %   check if the cost function works well  
4. %   check with the matlab fit function as standard  
5.   
6. %check cost function 2  
7. x=[1;2;3;4];  
8. y=[1.1;2.2;2.7;3.8];  
9.   
10. EXPR= {'x','1'};  
11. p=fittype(EXPR);  
12. parameter=fit(x,y,p);  
13.   
14. end

運行結果：

[cpp]  view plain copy

1. >> checkcostfunc()  
2.   
3. ans =   
4.   
5.      Linear model:  
6.      ans(x) = a*x + b  
7.      Coefficients (with 95% confidence bounds):  
8.        a =        0.86  (0.4949, 1.225)  
9.        b =         0.3  (-0.6998, 1.3)

和我們的結果一樣。下面畫圖：

[cpp]  view plain copy

1. function PlotFunc( xstart,xend )  
2. %PLOTFUNC Summary of this function goes here  
3. %   draw original data and the fitted   
4.   
5.   
6.   
7. %===================cost function 2====linear regression  
8. %original data  
9. x1=[1;2;3;4];  
10. y1=[1.1;2.2;2.7;3.8];  
11. %plot(x1,y1,'ro-','MarkerSize',10);  
12. plot(x1,y1,'rx','MarkerSize',10);  
13. hold on;  
14.   
15. %fitted line - 擬合曲線  
16. x_co=xstart:0.1:xend;  
17. y_co=0.3+0.86*x_co;  
18. %plot(x_co,y_co,'g');  
19. plot(x_co,y_co);  
20.   
21. hold off;  
22. end




註解：

1 single training example公式

                           

bp算法matlab線性迴歸結果分析_bp算法matlab線性迴歸結果分析_03


bp算法matlab線性迴歸結果分析_擬合_04


                         

                           


More than one training example:


θ：θ(i)-=gradient(i),其中gradient(i)是J(θ)對θi求導的函數式,此處令α=1/m，並且gradient(1)在matlab程序中實際對應x(0),而x(0)=1，把代入上面的公式可以得到gradient(1)=sum(delta)/m; 

註解2

1. options = optimset('GradObj','on','MaxIter',100);  
2.   initialTheta = zeros(2,1);  
3.   [optTheta,functionVal,exitFlag] = fminunc(@costFunction2,initialTheta,options);

初學matlab優化，迭代中止後，經常一頭霧水。參看幫助後仍似懂非懂。下面關於fminbnd函數的説明（也可作為fmincon函數的參考）對於新手也許會有幫助，不當之處請指正。
目標函數fun:
       需要最小化的目標函數。fun函數需要輸入標量參數x，返回x處的目標函數標量值f。可以將fun函數指定為命令行，如
             x = fminbnd(inline('sin(x*x)'),x0)
同樣，fun參數可以是一個包含函數名的字符串。對應的函數可以是M文件、內部函數或MEX文件。若fun='myfun'，則M文件函數myfun.m必須有下面的形式：
            function f = myfun(x)
            f = ...            %計算x處的函數值。
若fun函數的梯度可以算得，且options.GradObj設為'on'（用下式設定）,
            options = optimset('GradObj','on')
則fun函數必須返回解x處的梯度向量g到第二個輸出變量中去。注意，當被調用的fun函數只需要一個輸出變量時（如算法只需要目標函數的值而不需要其梯度值時），可以通過核對nargout的值來避免計算梯度值。

function [f,g] = myfun(x) 
  
f = ...          %計算x處得函數值。 
  
if nargout > 1   %調用fun函數並要求有兩個輸出變量。 
  
   g = ...       %計算x處的梯度值。 
  
end