文章目錄
- 基本介紹:
- 座標系變換運算規則:
- 關係運算説明:
- 座標系運算規則一:
- 座標系運算規則二:
- 齊次座標系:
- 齊次座標系下的座標變換:
- 眼在手外:
- 眼在手內:
- 解方程:
- - Tais方法
- 使用opencv完成手眼標定
- 歐拉角變換為旋轉矩陣:
- 旋轉矩陣變成歐拉角:
- 易錯點:
基本介紹:
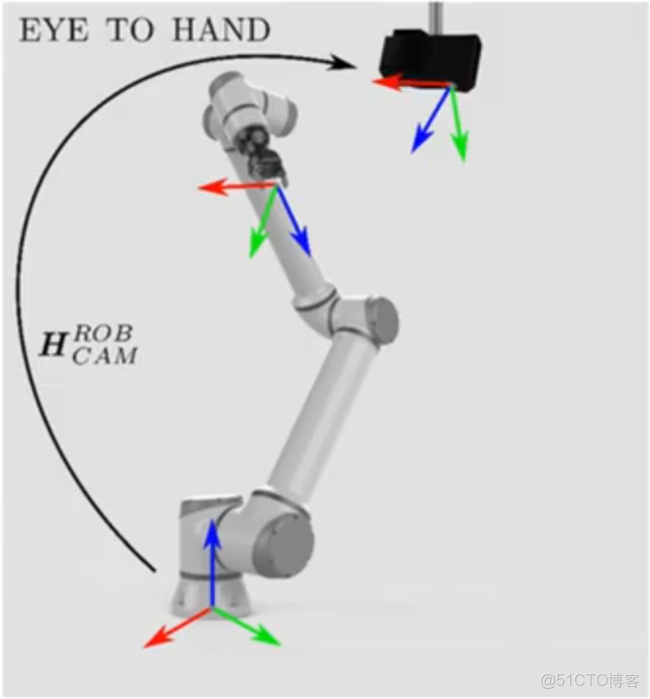
- 眼在手外(eye to hand):
相機固定在機械臂以外的地方,主要標定相機和基底座標系的轉換矩陣。 - 眼在手上(eye in hand):
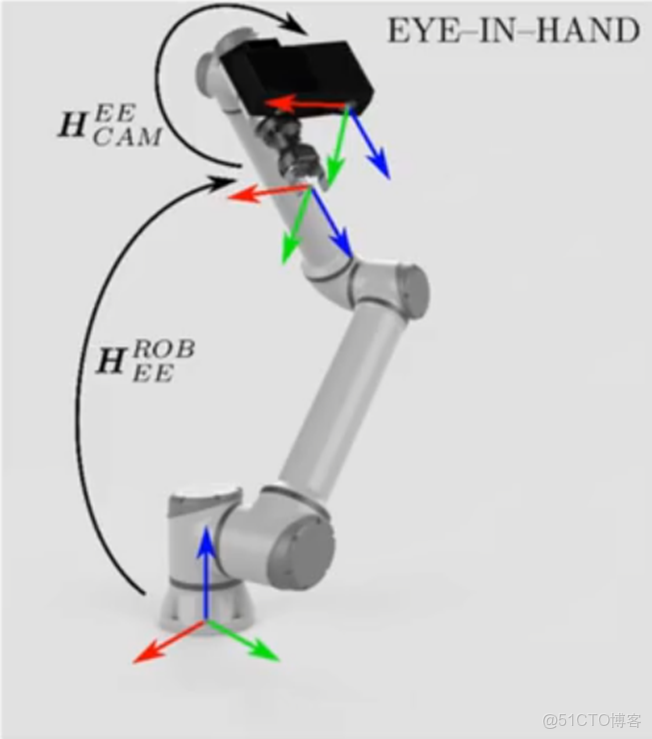
相機固定在機械臂末端,主要標定相機和機械臂末端的轉換矩陣。
座標系變換運算規則:



以上等價於:機械臂末端座標系在基底座標系下的描述
關係運算説明:

由於R是正交矩陣,正交矩陣的逆=正交矩陣的轉置,所以有時候也會寫為
座標系運算規則一:
假設有兩個座標系A,B,其中座標系B中的點b是由座標系A中的點a轉換來的,則點a和點b之間有如下等式

由以上等式可以看出:
座標系運算規則二:
假設由三個座標系A,B,C,已知如下關係:
對於旋轉矩陣
對於平移矩陣

齊次座標系:
- 已知座標系A下的點
,則點
的齊次座標系可以寫成
- 已知齊次座標系下一點
,則點
的真實三維座標為
- 齊次座標系下的變換矩陣:
齊次座標系下的座標變換:
- 已知a,b,c分別為座標系A,B,C下的齊次座標,則有如下關係:
眼在手外:
求解目標:機械臂基底座標系到相機座標系的變換矩陣
手眼標定座標系表示:
- 機械臂基底座標系 – base
- 機械臂末端座標系 – end
- 相機座標系 – camera
- 標定板座標系 – board
實現方法:
- 把標定板固定在機械臂末端
- 使用相機拍攝不同機械臂姿態下的標定板圖片n張,n>3
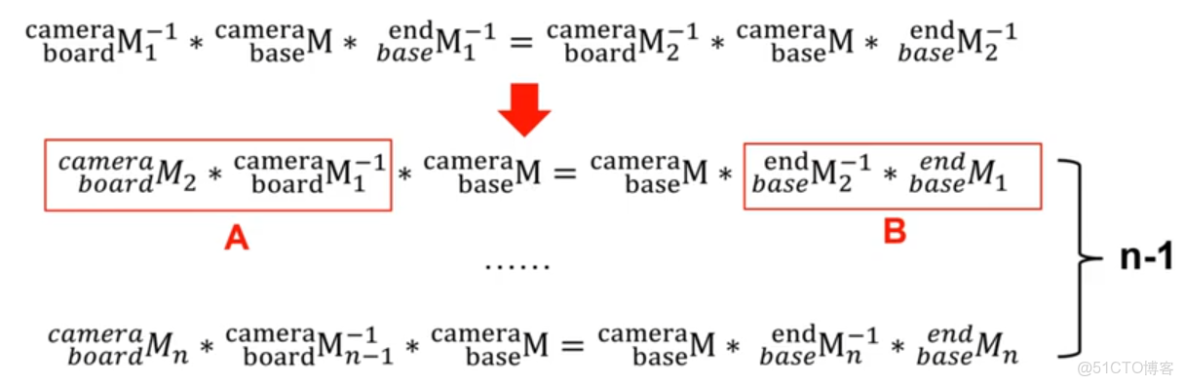
則對每張圖片可知:
變形得:
其中:
已知對每張圖片:

**則可以得到如下等式:**左乘
眼在手內:
求解目標:機械臂末端座標系到相機座標系的變換矩陣
手眼標定座標系表示:
- 機械臂基底座標系 – base
- 機械臂末端座標系 – end
- 相機座標系 – camera
- 標定板座標系 – board
實現方法:
- 把標定板放在固定位置不動
- 移動機械臂末端,從不同角度拍攝n張標定板圖片
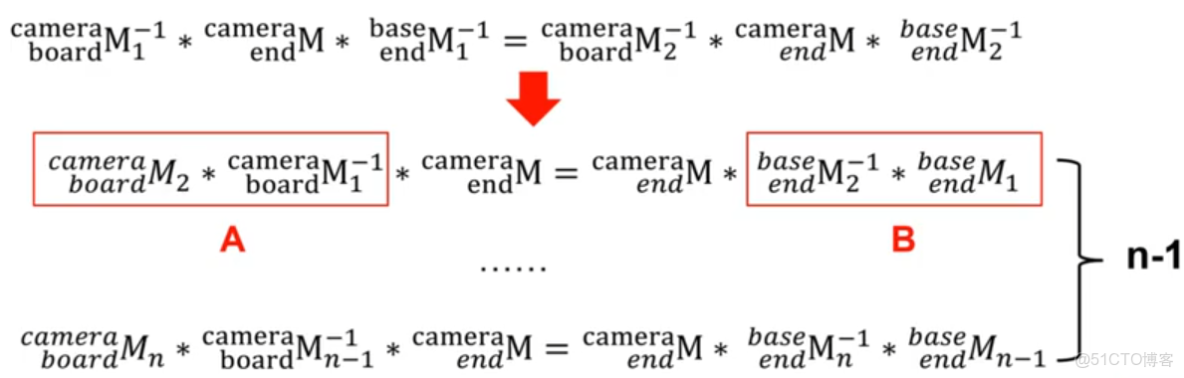
則對每張圖片可知:
變形得:
其中:
已知對每張圖片:

**則可以得到如下等式:**左乘
解方程:
無論是眼在手外還是眼在手內,都可以得到一個經典的方程組
其中X是我們要求得的手眼矩陣,裏面有6個線性無關的變量,其中旋轉3個自由度,平移3個自由度。
- Tais方法
**形式變換:**由於A,B,X均為變換矩陣

則

Tais方法:先求解Rx,再求解Tx
旋轉的表示:
**旋轉矩陣:**3*3矩陣
旋轉向量:
剛體繞旋轉軸旋轉,
表示的是旋轉軸的方向,
的長度表示剛體繞旋轉軸的角度
旋轉角:
旋轉角又稱歐拉角,一般情況下旋轉角指的是座標系繞x軸旋轉後,再繞y軸旋轉後,再繞z軸旋轉分別的角度
使用opencv完成手眼標定
歐拉角變換為旋轉矩陣:
旋轉矩陣變成歐拉角:
solvePnP()
bool cv::solvePnP(InputArray objectPoints,
InputArray imagePoints,
InputArray cameraMatrix, // 相機內參
InputArray distCoeffs, // 相機畸變係數
OutputArray rvec, // R
OutputArray objectPoints, // T
bool useExtrinsicGuess = false,
int flags = SOLVEPNP_ITERATIVE)易錯點:
1. 利用calibrateCamera函數中計算的R、T,來作為標定板座標系到相機座標系的輸入
問題分析:對手眼標定來説,這個R、T沒有問題。但是由於後續的抓取來説,使用的物體三維座標是相機重建的點雲,即相機之前標定的內參下的點雲。此時手眼標定的相機座標系和實際抓取使用的相機座標系輕微的不一致,導致抓取總是有輕微誤差。
2. 識別標定板角點方向反了!
由於在建立棋盤格上的三維座標系的時候,我們默認是從棋盤格左上角到右下角建立的,如果識別反了,則會有個別圖片棋盤格識別的角點和輸入的棋盤格三維座標對應不上!