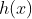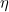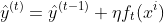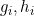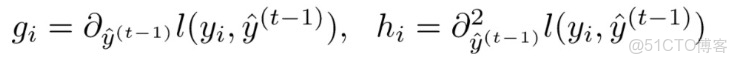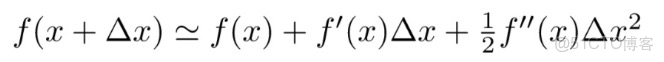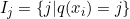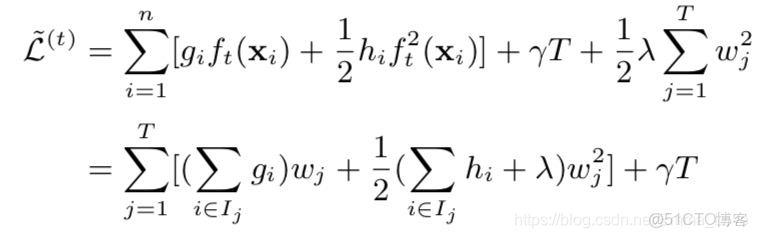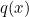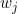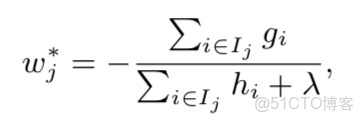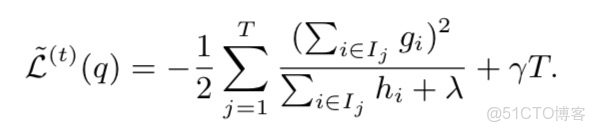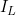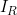GBDT和XGBoost在工業界和競賽界有着廣泛的應用。雖然使用起來並不難，但若能知其然也知其所以然，則會在使用時更加得心應手。本文主要是根據對陳天奇大神的PPT和原始論文的學習，梳理一下GBDT和XGBoost的“知識點”。

首先我們先列出CART，GB，GBDT和XGBoost之間的關係。

  • CART是分類與迴歸樹（Classification and Regression Trees），是決策樹的一種，既能做分類，又能做迴歸。在分裂過程中會用Gini值作為純度的評估標準。
  • Gradient Boosting（GB）算法：是Boosting算法的一種，具體稍後介紹。
  • GBDT（Gradient Boosting Decision Tree）：正如其名字一樣，GBDT是GB與DT的集合，這裏面GB代表Gradient boosting算法，DT代表decision tree算法，GBDT就是使用CART作為基學習器的GB算法。
  • XGBoost：xgboost擴展和改進了GDBT，xgboost算法更快，準確率也相對高一些。

接下來，我們將詳細的介紹GB，GBDT和XGBoost算法，CART將放到決策樹一塊進行介紹。

陳天奇大神的PPT：《Introduction to Boosted Trees》

目錄

0. CART

1. 梯度增強 Gradient Boosting (GB)

2. GBDT

3. XGBoost

3.1 XGBoost的學習過程 

3.2 XGBoost推導

3.3 如何構建樹結構 —— 分裂節點的算法？

3.3.1 Greedy Learning of the tree

3.2.2 Approximate Algorithm

4. 針對稀疏數據的算法——缺失值處理

5. XGBoost減小過擬合的方式

6. XGBoost的優點

7. XGBoost vs. GBDT

0. CART

CART（Classification and Regression Trees，分類與迴歸樹，簡稱迴歸樹）也是一種樹模型，它既能解決分類問題，也能處理迴歸問題。

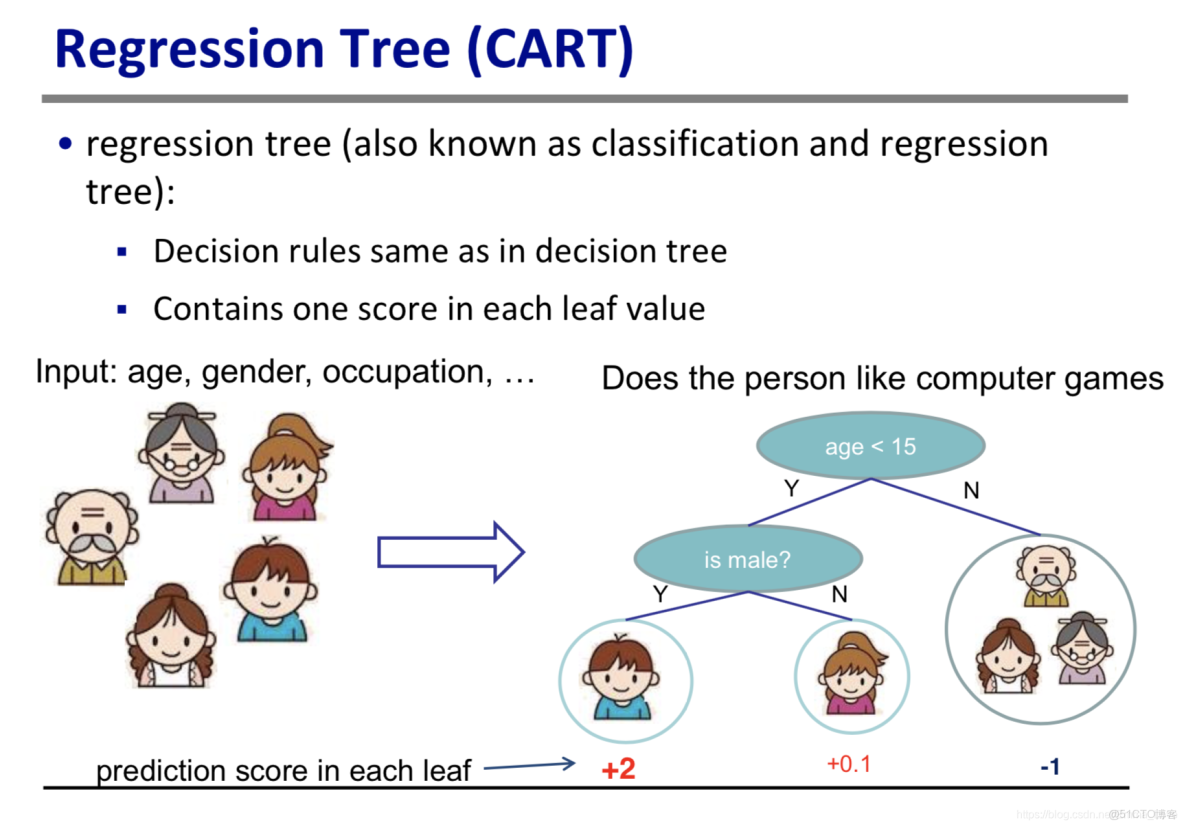
參照陳大神的PPT，對迴歸樹有一個直觀的感受。

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_CART

可以看到，迴歸樹與分類樹有很多相似之處，例如：都是樹形結構，每個非葉子節點可以代表一個條件判斷。

與分類樹不同的是，

  • 分類樹葉子節點給出的是類別標籤；而回歸樹的葉子節點會給出一個score，根據這個得分可以進行分類或者回歸。
  • 迴歸樹在節點劃分的過程中，不適用信息熵或Gini指數作為特徵好壞的評估標準，而是使用一種啓發式的操作，利用最小化均方差來進行評估。下面給出一個對比：

分類樹 vs. 迴歸樹的劃分方法

                                      分類樹

                                     迴歸樹

以C4.5為例，在分裂出新的分枝時，採用Gini指數評估樣本純度。

具體過程如下：

與分類樹不同的是，迴歸樹在分裂出新的分枝時，不使用Gini指數，而是使用最小化均方差進行衡量特徵的好壞，即：

                           

其中，

代表劃分到該劃分單元上的樣本集合，

是每個劃分單元的預測值 —— 即該單元內每個樣本點的值的均值：                     

那麼：最優切分變量j和最優切分點s的求解可以用下面的式子進行：

         

 

其中，

和

是被劃分後的兩個區域。

具體流程：

1.  從根節點開始，對節點計算現有特徵的Gini指數，對每一個特徵，例如A，再對其每個可能的取值如a，根據樣本點對

的結果的”是“與”否“劃分為兩個部分，利用下述公式進行計算。

 

2. 在

特徵A以及該特徵

可能取值a中，選擇Gini指數最小的特徵及其對應的取值作為最優特徵和最優切分點。然後根據最優特徵和最優切分點，將本節點的數據集二分，生成兩個子節點。

3. 對兩個字節點遞歸地調用上述步驟，直至節點中的樣本個數小於閾值，或者樣本集的基尼指數小於閾值，或者沒有更多特徵後停止；生成CARTCART分類樹；

 

4. 若最後某葉子節點包括多種類別的樣本，則以樣本數最多的類別為最後的標記。

 

 

 

1. 梯度增強 Gradient Boosting (GB)

GB算法是Boosting算法的一種。

Boosting算法的學習過程採用的思想是Additive Manner（加法效應），即：迭代生成多個（K個）弱學習器，然後將弱模型的結果相加，其中後面的模型是基於前面的模型的效果生成的，模型間的關係以及最後的預測結果如下：

公式（1.1）


公式（1.2）

可以看到，Boosting算法是通過一系列的迭代來優化分類結果，每迭代一次引入一個新的弱分類器，來克服現在已經存在的弱分類器組合的shortcomings，即：每一次迭代都致力於減少偏差。

  • Adaboost vs. Gradient Boosting

Adaboost和Gradient Boosting是兩種boosting算法，他們的區別就在於如何選擇

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_CART_02

,即：採用何種策略來克服前面已有的shortcoming。

Adaboost採取的策略是在每一次新的迭代中，增加上一輪分類錯誤的樣本的權重以提高對這些樣本的關注程度。

Gradient Boosting算法在迭代的時候將負梯度作為上一輪基學習器犯錯的衡量指標，在下一輪學習中通過擬合負梯度來糾正上一輪犯的錯誤。

Question：為什麼可以採用負梯度作為衡量指標呢？

Answer：

這就需要結合梯度下降方法進行分析啦。機器學習的學習過程就是通過優化算法找到使得損失函數

最小的參數

。梯度下降方法的更新公式：

 

GB算法的學習過程也是基於Additive Manner（加法模型）的，因此在第k步的目標是最小化損失函數

，進而求得相應的基學習器。若將

作為參數，則可以同樣適用梯度下降法：對比公式（1.1）和（1.4），可以發現若將

，即：用基學習器

擬合前一輪模型損失函數的負梯度，就是通過梯度下降法最小化

。由於

實際為函數，所以該方法被認為是函數空間的梯度下降。

 

負梯度也被稱為“響應 (response)”或“偽殘差 (pseudo residual)”。殘差

越大，表明前一輪學習器

的結果與真實值

相差較大，那麼下一輪學習器通過擬合殘差或負梯度，就能糾正之前的學習器犯錯較大的地方。


公式（1.3）

  • GB算法的步驟：

step 1. 初始化：

               

step 2. for k = 1 to K:

                  (a). 計算負梯度： 

                         

                   (b). 通過最小化平法誤差，用基學習器

擬合

：                         

 

                   (c). 使用line search確定步長，以使得

最小:                         

                   (d). 求得

:                        

step 3. 輸出 

2. GBDT

GBDT（Gradient Boosting Decision Tree）是以決策樹（CART）為基學習器的GB算法。

注意：GBDT不論是用於分類還是迴歸，使用的決策樹都是迴歸樹。

GBDT中的決策樹是弱模型，深度較小一般不會超過5，葉子節點的數量也不會超過10，對於每棵樹乘上比較小的縮減係數shrinkage（學習率<0.1），有些GBDT的實現加入了隨機抽樣（subsample 0.5<=f <=0.8）提高模型的泛化能力。通過交叉驗證的方法選擇最優的參數。因此GBDT實際的核心問題變成怎麼基於

和CART生成

。

再次強調GBDT使用的是迴歸樹。迴歸樹和分類樹在分裂出新的分枝時是不同的。其對比見第0. CART節的表格1。

3. XGBoost

XGBoost算法的步驟與GBDT基本相同，不同之處主要有：

  • GBDT只利用了一階導數的信息，而XGBoost使用了一節倒數和二階導數，迭代生成基學習器。XGBoost對損失函數進行二階泰勒展開。
  • XGBoost為損失函數添加正則項，以減少過擬合的風險

接下來，基於陳大神的PPT和論文來詳細介紹XGBoost的損失函數，以及學習/訓練過程，及公式的推倒過程。

3.1 XGBoost的學習過程 

  •   XGBoost的損失函數:

    

公式（3.1）

可以看到該損失函數由兩部分組成，分別是：經驗損失和正則項。其中，K代表分類器的個數，n代表樣本的個數，f代表基分類器。

  •  XGBoost的學習過程：

由於是樹結構模型，所以不能使用SGD等優化算法進行優化。其優化過程與Boosting一樣，採用的是Additive Training（加法效應）：

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_機器學習_03

注意：

雖然現在給出的是在每輪迭代中，直接向已有分類結果中添加新分類器的預測結果。但是實際上，XGBoost會為每輪的結果添加一個衰減權重

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_CART_04

（就是learning rate）即：

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_機器學習_05

，這可以使得每一棵樹的影響力不會太大，留下更大的空間給後面生成的樹去優化模型。

3.2 XGBoost推導

  • 1. 定義損失函數

在第t次迭代的損失函數可以寫成：

公式（3.2）

由公式（3.2）可以看出，迭代過程是一個貪婪學習的過程，即添加最能夠改進公式（3.2）的損失函數的

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_GBDT_06

。

  • 2. 利用泰勒公式進行變換

定義

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_XGBoost_07

分別為上一輪損失函數關於

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_XGBoost_08

的一階倒數和二階導數，

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_GBDT_09

基於二階泰勒展開公式:

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_GBDT迴歸預測實驗報告_10

，

將公式（3.2）進行變換，可以得到新的損失函數：

 

公式（3.3）

  • 3. 定義正則項，描述XGBoost的結構複雜度：

公式（3.4）

其中T代表葉子節點的數量，w代表葉子節點的權重。

  • 4. 按照葉子節點的劃分改寫目標函數：

定義在葉子節點j中的樣本集合為：

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_機器學習_11

，q代表該葉子節點所在的樹。

  

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_GBDT迴歸預測實驗報告_12

公式（3.5）

  • 4. 對目標函數求解：

對於給定的樹結構

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_GBDT迴歸預測實驗報告_13

，那麼每個葉節點的最優權重w可以通過公式3.5求出，即：對所有

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_CART_14

求導，並令其導數為0,即可求解。

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_GBDT_15

公式（3.6）

如此，損失函數可以被進一步改寫為下面的公式。該公式可以用來度量樹的結構的好壞。其中，L越小，説明結構越好。

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_機器學習_16

公式（3.7）

3.3 如何構建樹結構 —— 分裂節點的算法？

與GBDT類似，XGBoost在劃分的時候也不使用Gini係數作為衡量劃分的好壞。

XGBoost採用的評估標準如下：

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_機器學習_17

公式（3.8）

其中，

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_CART_18

, 

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_XGBoost_19

代表劃分到左右節點的樣本集合。

3.3.1 Greedy Learning of the tree

算法1給出了利用貪婪算法來劃分樹的分枝。

注意：為了提高效率，在計算前會對樣本在給定特徵上按照值得大小進行排序。這樣，在計算時就可以直接使用排序好的樣本，進而提高計算速度。

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_XGBoost_20

3.2.2 Approximate Algorithm

對於連續型特徵值，當樣本數量非常大，該特徵取值過多時，遍歷所有取值會花費很多時間，且容易過擬合。因此XGBoost思想是對特徵進行分桶，即找到l個劃分點，將位於相鄰分位點之間的樣本分在一個桶中。在遍歷該特徵的時候，只需要遍歷各個分位點，從而計算最優劃分。

從算法偽代碼中該流程還可以分為兩種：

  • 全局的近似是在新生成一棵樹之前就對各個特徵計算分位點並劃分樣本，之後在每次分裂過程中都採用近似劃分
  • 局部近似就是在具體的某一次分裂節點的過程中採用近似算法。

GBDT迴歸預測實驗報告 gbdt分類與迴歸的區別_機器學習_21

4. 針對稀疏數據的算法——缺失值處理

當樣本的第i個特徵值缺失時，無法利用該特徵進行劃分時，XGBoost的想法是將該樣本分別劃分到左結點和右結點，然後計算其增益，哪個大就劃分到哪邊。具體見算法3.

5. XGBoost減小過擬合的方式

  1. 在損失函數中添加正則項
  2. 在Additive Training中，在每次迭代的過程中，為新添加的函數指定一個縮減權重，這可以使得每一棵樹的影響力不會太大，留下更大的空間給後面生成的樹去優化模型。即：
  3. Column Sampling: 類似於隨機森林中的選取部分特徵進行建樹。其可分為兩種，一種是按層隨機採樣，在對同一層內每個結點分裂之前，先隨機選擇一部分特徵，然後只需要遍歷這部分的特徵，來確定最優的分割點。另一種是隨機選擇特徵，則建樹前隨機選擇一部分特徵然後分裂就只遍歷這些特徵。一般情況下前者效果更好。

6. XGBoost的優點

  1. 使用許多策略去防止過擬合，如：正則化項、Shrinkage and Column Subsampling等。
  2. 目標函數優化利用了損失函數關於待求函數的二階導數
  3. .支持並行化，這是XGBoost的閃光點，雖然樹與樹之間是串行關係，但是同層級節點可並行。具體的對於某個節點，節點內選擇最佳分裂點，候選分裂點計算增益用多線程並行。訓練速度快。
  4. 添加了對稀疏數據的處理。
  5. 交叉驗證，early stop，當預測結果已經很好的時候可以提前停止建樹，加快訓練速度。
  6. 支持設置樣本權重，該權重體現在一階導數g和二階導數h，通過調整權重可以去更加關注一些樣本。

7. XGBoost vs. GBDT

  1. 傳統的GBDT以CART樹作為基學習器，XGBoost還支持線性分類器，這個時候XGBoost相當於L1和L2正則化的邏輯斯蒂迴歸（分類）或者線性迴歸（迴歸）；
  2. 傳統的GBDT在優化的時候只用到一階導數信息，XGBoost則對代價函數進行了二階泰勒展開，得到一階和二階導數
  3. XGBoost在代價函數中加入了正則項，用於控制模型的複雜度。從權衡方差偏差來看，它降低了模型的方差，使學習出來的模型更加簡單，放置過擬合，這也是XGBoost優於傳統GBDT的一個特性；
  4. shrinkage（縮減），相當於學習速率（XGBoost中的eta）。XGBoost在進行完一次迭代時，會將葉子節點的權值乘上該係數，主要是為了削弱每棵樹的影響，讓後面有更大的學習空間。（GBDT也有學習速率）；
  5. Column Subsampling列抽樣。XGBoost借鑑了隨機森林的做法，支持列抽樣，不僅防止過 擬合，還能減少計算；
  6. 對缺失值的處理。對於特徵的值有缺失的樣本，XGBoost還可以自動 學習出它的分裂方向；
  7. XGBoost工具支持並行。Boosting不是一種串行的結構嗎?怎麼並行 的？注意XGBoost的並行不是tree粒度的並行，XGBoost也是一次迭代完才能進行下一次迭代的（第t次迭代的代價函數裏包含了前面t-1次迭代的預測值）。XGBoost的並行是在特徵粒度上的。我們知道，決策樹的學習最耗時的一個步驟就是對特徵的值進行排序（因為要確定最佳分割點），XGBoost在訓練之前，預先對數據進行了排序，然後保存為block結構，後面的迭代 中重複地使用這個結構，大大減小計算量。這個block結構也使得並行成為了可能，在進行節點的分裂時，需要計算每個特徵的增益，最終選增益最大的那個特徵去做分裂，那麼各個特徵的增益計算就可以開多線程進行。