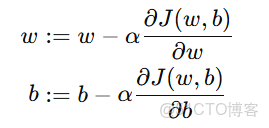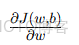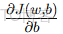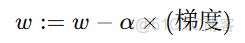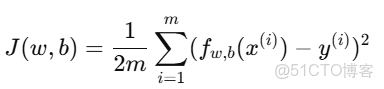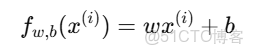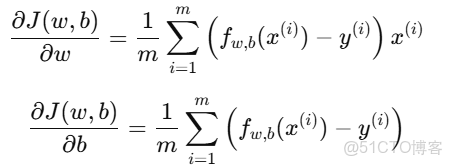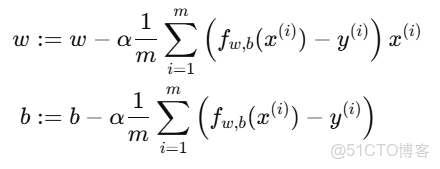一、梯度下降（Gradient Descent）

1. 基本概念

梯度下降（Gradient Descent） 是一種用於 最小化代價函數 J(w,b)J(w,b)J(w,b)的優化算法。

它的思想相當直觀：

環顧四周，選擇讓代價函數下降最快的方向，然後沿着該方向走一步。然後在新的位置重複這個過程，直到到達最低點。這種“下山”的過程，就是梯度下降。

2. 核心思想（Intuition）

假設你站在一座山上，天氣太黑看不清地形。你只能摸索坡度最陡的方向（即梯度方向的反方向）一步步往下走。

• 每次往下走一步，就更新當前點的位置。
• 最終到達的山谷底部，就是代價函數的最小值。

這個最小點被稱為：

局部最小值（Local Minimum）
凸函數（如線性迴歸中的碗狀函數），那麼局部最小值同時也是就是如果代價函數全局最小值（Global Minimum）。

3. 參數更新公式（Update Rule）

梯度下降通過不斷調整參數 w 和 b，讓代價函數 J(w,b) 逐步減小。

公式如下：

其中：

符號	含義
α	學習率（Learning Rate）
	對權重 w 的偏導數（梯度）
	對偏置 b 的偏導數
“:=”	表示賦值更新

補充： 同步更新的重要性

更新時，w 和 b 必須同時更新（Simultaneous Update）：

• 不應先更新 w 再用新的 w 去計算 b；
• 否則會導致不一致的結果，收斂路徑混亂。

4. 梯度方向與代價變化

• 梯度（Gradient）表示函數上升最快的方向。
• 因此，大家沿着梯度的反方向更新參數，才能讓代價下降。

數學上：

• 當梯度為正：説明函數在該點處上升 → 我們應減小 w
• 當梯度為負：説明函數在該點處下降 → 我們應增大 w

通過不斷調整，J(w,b) 的值會持續減小，直到達到最小點。

5. 學習率 α\alphaα 的選擇

學習率（Learning Rate）控制了每一步的前進速度。

學習率大小	效果	圖示描述
太小	下降速度慢，訓練時間長	緩慢接近最低點
太大	可能跨過最低點，甚至震盪發散	跳過碗底
合適	穩定快速收斂	順滑下降到最小值

當代價函數到達最小點時：
梯度 =0，此時更新量為 0，w,b 不再變化。

示意圖：

學習率太小 → 慢慢下降到谷底

學習率太大 → 直接跳過谷底、來回震盪

---

二、線性迴歸的梯度下降（Gradient Descent for Linear Regression）

1. 代價函數回顧

線性迴歸的代價函數定義為：

其中：

2.梯度公式推導

我們要求出代價函數對 w 和 b 的偏導數：

3.參數更新公式（線性迴歸專用）

將梯度代入更新規則：

4.特點分析

• 代價函數是凸函數（Convex Function）

• 形狀像一個“碗”；
• 沒有多個局部最小值；
• 因此梯度下降一定能收斂到全局最優解。

• 每次更新都讓 J(w,b) 更小

• 利用迭代逐步逼近最優參數。

5. 舉例説明（Intuitive Example）

假設我們在訓練一個簡單的線性模型來預測房價：

x（房屋面積）	y（房價）
50	150
100	300
150	450

初始參數： w=0,b=0

每次迭代：

1. 根據當前 w,b 計算預測值；
2. 計算誤差（預測 - 實際）；
3. 計算代價函數 J(w,b)；
4. 根據梯度更新 w,b。

經過若干次更新後，模型會逐步收斂到最佳擬合直線。

6.小結（Summary）

項目	內容
目標	最小化代價函數 J(w,b)J(w,b)J(w,b)
更新規則	w:=w−α∂J∂ww := w - \alpha \frac{\partial J}{\partial w}w:=w−α∂w∂J，b:=b−α∂J∂bb := b - \alpha \frac{\partial J}{\partial b}b:=b−α∂b∂J
學習率	控制更新步長
同步更新	w,bw,bw,b 同時更新
可視化	曲面下降、等高線收斂
線性迴歸的特性	代價函數為凸函數，僅有一個全局最小值