簡介

三分圖染色指對於一個圖進行三種顏色的染色，每條邊的兩個端點顏色不同
本文旨解決 m-n≤7的染色問題，即邊數只比點數多7

做法

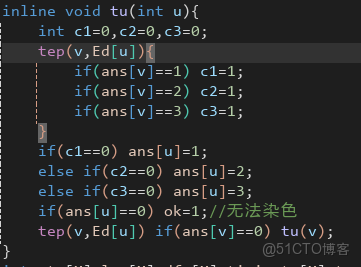
考慮對於每個度數≥3的結點作暴力dfs染色，

代碼差不多就是這樣的

即能染顏色1就染顏色1，能染顏色2就染顏色2，能染顏色3就染顏色3.

出發點的選擇

發現當一個結點染色失敗時需要至少三條邊與其相連，而如果圖上只有一個度數大於等於三的點，
直接從這個點出發一定可以直接暴力染完所有度數為1，2的點
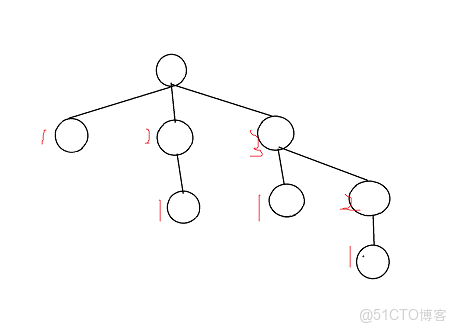
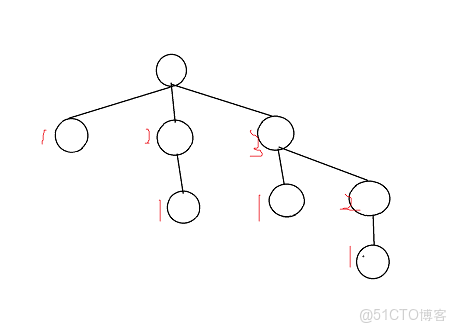
考慮分析有兩個度數為三的點要相互染色失敗

染色

考慮當一個度數為三的節點暴力染色失敗後的樣子：

最上方的點無法染色，因為下方的三個點已經被被迫染上了三種顏色，

下方的結點一定染色成1，2，3，那麼再下方的結點一定會把1，2的位置填滿

由於bfs暴力染色所以考慮先訪問該點下方1，2，3，最後訪問無法染色的結點，所以需要返祖邊

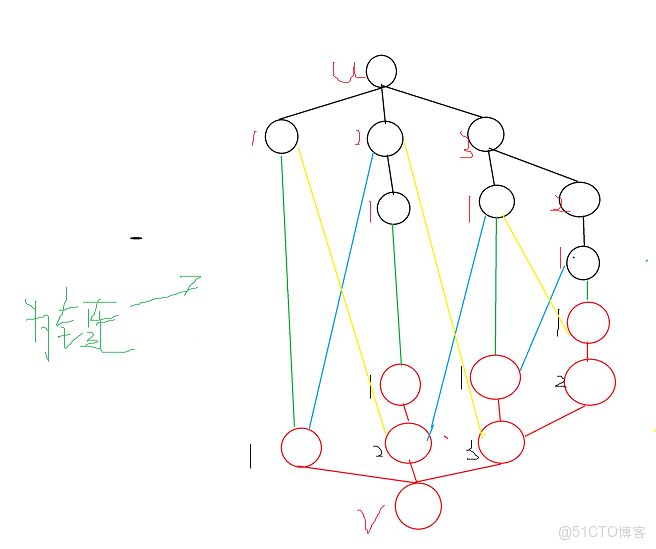
中間的綠色為本來連通圖的鏈接邊

由於要返祖，所以向下後需要退回到另一條鏈上，上下的u，v有四條關鍵邊，所以上下分別需要6條返祖邊

6條返祖邊會出現12個度數為三的點，加上原來要形成

結構需要兩個三度點

所以形成一對互相染色失敗的點共需要2+2+12個三度點，16個三度點在m-n=7時存在一個，當m-n=7時最多16個三度點

但是不是所有的三度點都會失敗，因為共有16個

所以直接把所有度數為三的點暴力向下染色，當有正確答案時一定可以找到正確的答案

已知n+7=m，即會出現8條返祖邊，最多16個度數為三的點