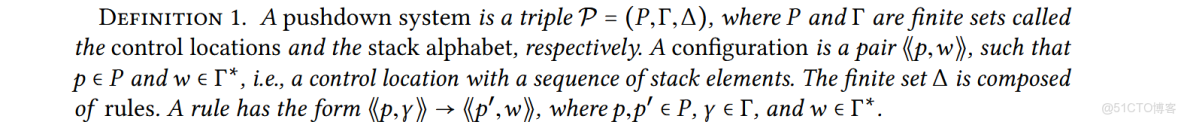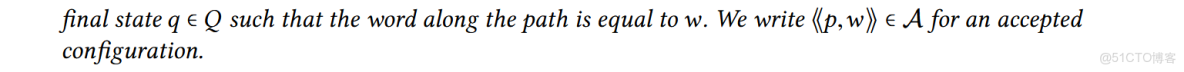Introduction

傳統的使用 AccessPath 的字段敏感分析在面臨循環字段引用（cyclic field reference）時存在路徑爆炸的問題，比如對於 JDK 8 中 TreeMap 的實現：

函數 rotateLeft 在函數 fixAfterInsertion 的 while 循環中被調用，rotateLeft 的 16, 17, 19, 20 行就是一個循環字段引用的案例。由於路徑不敏感，靜態分析會過近似地認為任意一個 由字段 left, right, parent 組成的任意長度的 AccessPath 都可能被寫入 value，即 \(T = \{this.f_1.f_2. ... .f_n | f_k \in \{ \text{left, right, parent} \}, 1 \leq k \leq n \in N\}\)。

在實際實現中，靜態分析使用 k-limit 限制 AccessPath 的長度，但這仍然導致巨大的開銷。

SPDS 使用兩個下推系統 field-PDS 和 call-PDS 解決字段敏感和上下文敏感，並同步他們的結果。把複雜度從 \(|\mathbb{F}^{3k}|\) 降低到 \(|\mathbb{S}||\mathbb{F}|^2\)。

A short introduction to pushdown systems

下推系統的定義如下：

\(w\) 的長度 \(|w|\) 決定了規則是 push 規則，pop 規則還是 normal 規則，因為會用 \(w\) 作為新的棧頂元素取代 \(\gamma\)。

一個用於上下文敏感和流敏感數據流分析的 call-PDS 可以被定義為 \(\mathcal{P}_{\mathbb{S}} = (\mathbb{V}, \mathbb{S}, \delta_{\mathbb{S}})\)。\(\mathbb{V}\) 是程序變量，\(\mathbb{S}\) 是程序 statement。Normal 規則對過程內的 flow function 做建模，push 和 pop 規則對過程間的轉移規則做建模，並處理上下文敏感。常規規則還可以捕獲控制流的語義，使得 \(\mathcal{P}_{\mathbb{S}}\)

下表給出了一個過程內的 flow function 的例子 assignFlow：

表中涵蓋了四種情況：第一種情況表示正在追蹤變量 \(x\) 但 \(x\) 的舊數據流已經被新的數據流覆蓋，所以返回空集表示不再追蹤；第二種情況表示正在追蹤變量 \(y\)，\(y\) 又被賦值給了 \(x\)，所以接下來需要同時追蹤 \(x\) 和 \(y\)，返回集合 \(\{x, y\}\)；assignFlow 是字段不敏感的，所以對於最後兩個情況，輸出的集合都是 \(\{x, y\}\)。對於 call-PDS，如果當前這個 statement 是 \(s\)，控制流下一個 statement 是 \(t\)，那麼對於 \(assignFlow(x, s)\) 中返回的集合中任意一個元素 \(y\)，都有一個對應的 normal 規則 \(\langle \langle x, s \rangle \rangle \rightarrow \langle \langle y, t \rangle \rangle\)。

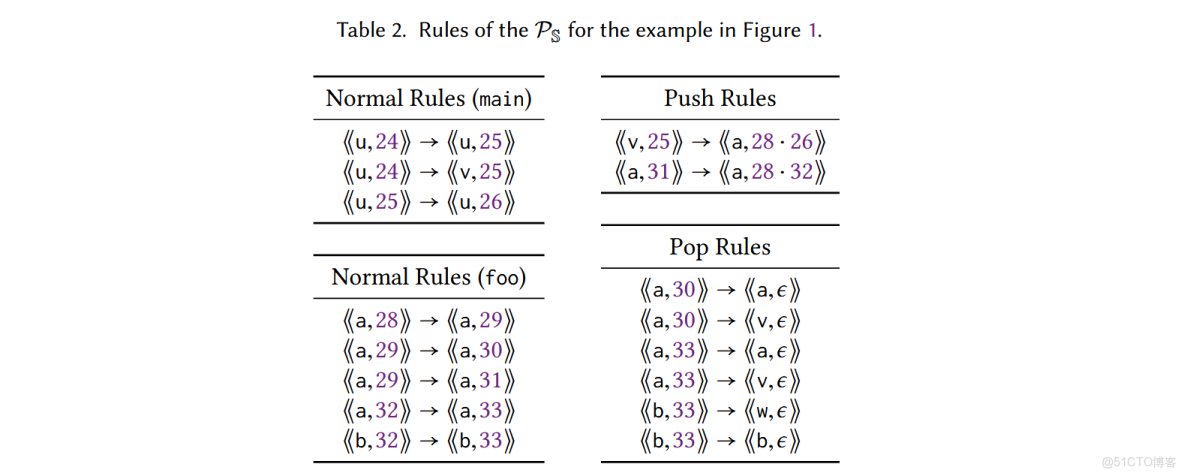
下面給出了一個過程間數據流及遞歸調用的例子：

Normal 規則比較簡單。Push 規則 \(\langle \langle v, 25 \rangle \rangle \rightarrow \langle \langle a, 28 · 26 \rangle \rangle\) 表示當數據流到達第 25 行的變量 \(v\)

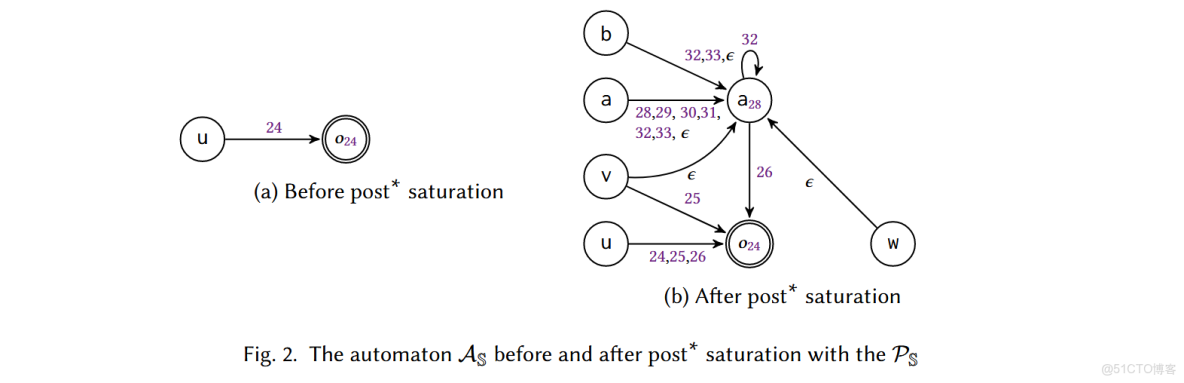
call-PDS 上存在轉移關係：如果 \(\langle \langle p, \gamma \rangle \rangle \rightarrow \langle \langle p', \omega \rangle \rangle\)，那麼對於任意的串 \(\omega'\) 都有 \(\langle \langle p, \gamma \omega' \rangle \rangle \rightarrow \langle \langle p', \omega \omega' \rangle \rangle\)，這個轉移關係刻畫了 PDS 在棧上做的操作。從一個起始 configuration \(c\) 出發，不斷應用規則，可以得到一個 \(c\) 可達的 configuration 集合 \(post*(c) = \{c' | c \Rightarrow^* c'\}\)（\(\Rightarrow^*\)

自動機 \(\mathcal{A}\) 描述了可達 configuration 集合。有算法 \(post*\) 可以以一個只接受初始 configuration 的自動機和一組規則為參數，構建出自動機 \(\mathcal{A}\)。

如果我們想知道“從語句 s 處的變量 v 開始，數據會流到哪裏去？”。我們構建一個只接受格局 \(\langle \langle v, s \rangle \rangle\) 的初始自動機，然後使用 \(post*\) 算法，檢查 \(\langle \langle v, s' \rangle \rangle\)

本質上是 IFDS？中間缺了一些步驟

Field-PDS

類似的，\(\mathcal{P}_{\mathbb{F}}\) 的 configuration 是 \(\langle \langle x @ s, f_0f_1...f_n \rangle \rangle\)，可以被理解為從 statement \(s\) 之後，追蹤 \(x.f_0f_1f_n\)