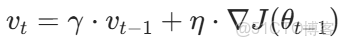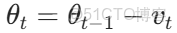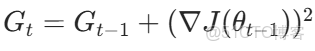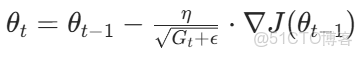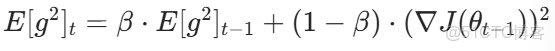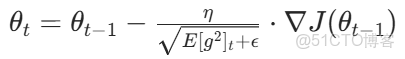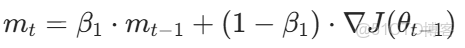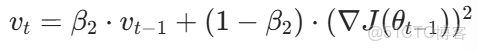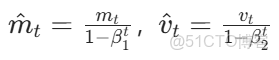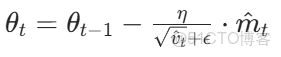一、動量優化器(Momentum)
1、核心思想
模擬物理中的 “動量” 概念,通過積累歷史梯度的 “慣性” 來加速收斂,減少震盪。
解決 SGD(隨機梯度下降)在溝壑區域(梯度方向頻繁變化)收斂慢、震盪大的問題。
2、公式
(1)動量變量(積累歷史梯度)
(2)參數更新
其中,γ為動量因子(通常取 0.9,控制歷史梯度的權3、重);η為學習率;∇J(θ)為當前參數的梯度
3、優點
(1)加速收斂:在梯度方向一致的區域(如平緩坡),積累動量加速更新
(2)減少震盪:在梯度方向頻繁變化的區域(如溝壑),通過歷史動量平滑更新方向
4、缺點
(1)動量因子γ和學習率η需要手動調參
(2)可能在局部最優附近因慣性 “衝過” 最優解
5、適用場景
適用於損失函數曲面較複雜(存在溝壑、震盪)的場景,如計算機視覺任務(圖像分類、目標檢測)
二、AdaGrad 優化器
1、核心思想
自適應學習率:對不同參數根據其歷史梯度平方和調整學習率 —— 梯度大的參數(頻繁更新)學習率衰減快,梯度小的參數(稀疏更新)學習率衰減慢。
適合處理稀疏數據(如自然語言處理中的 one-hot 向量)。
2、公式
(1)歷史梯度平方和積累
(2)參數更新
其中,ϵ 為極小值(如 10−8),避免分母為 0;η 為初始學習率(通常取 0.01)。
3、優點
(1)自適應學習率,無需手動調整
(2)對稀疏特徵更友好(學習率衰減慢,保留更新能力)
4、缺點
(1)學習率單調遞減,訓練後期可能因學習率過小導致收斂停滯
(2)對非稀疏數據效果一般
5、適用場景
稀疏數據任務:如文本分類、推薦系統(用户 - 物品交互稀疏)
三、RMSprop 優化器
1、核心思想
改進 AdaGrad 的 “學習率單調遞減” 問題,通過指數移動平均(EMA)計算曆史梯度平方和,僅保留近期梯度的影響,避免學習率過早衰減。
2、公式
(1)歷史梯度平方的指數移動平均
(2)參數更新
其中,β 為衰減係數(通常取 0.9),控制歷史梯度的遺忘速度。
3、優點
(1)解決 AdaGrad 學習率過早衰減的問題,訓練後期仍能有效更新
(2)自適應學習率,對非稀疏數據更友好
4、缺點
(1)仍需手動設置初始學習率 η
(2)缺乏動量機制,可能在震盪區域收斂較慢
5、適用場景
非稀疏數據任務:如語音識別、圖像生成(像素級密集數據)
三、Adam 優化器
1、核心思想
結合動量優化器(一階矩估計,處理梯度方向)和RMSprop(二階矩估計,處理學習率自適應)的優點,同時計算梯度的一階矩(均值)和二階矩(未中心化方差),動態調整更新方向和步長。
2、公式
(1)一階矩(動量,梯度均值)
(2)二階矩(梯度平方的指數移動平均)
(3)偏差修正(解決初始時刻矩估計接近 0 的問題)
(4)參數更新:
3、優點
(1)結合動量和自適應學習率,收斂快且穩定
(2)對超參數(如學習率)不敏感,默認參數在多數任務中表現良好
(3)適用於稀疏數據和非稀疏數據
4、缺點
(1)在某些場景(如生成對抗網絡 GAN)中可能收斂到局部最優,需結合其他策略(如學習率調度)
(2)計算量略大於 SGD,但通常可接受
5、適用場景
幾乎所有深度學習任務:自然語言處理(Transformer)、計算機視覺(CNN)、強化學習等,是目前最常用的優化器之一。