文章目錄
- 簡要介紹
- 相關例題
- 二分查找
- 題目描述
- 題目分析
- 實現思路
- 實現代碼
- 在排序數組中查找元素的第一個和最後一個位置
- 題目描述
- 題目分析
- 實現思路
- 實現代碼
- 小技巧
- 搜索插入位置
- 題目描述
- 題目分析
- 實現思路
- 實現代碼
- 代碼一
- 代碼二
- [x 的平方根 ](https://leetcode.cn/problems/sqrtx/)
- 題目描述
- 題目分析
- 實現思路
- 實現代碼
- 代碼一
- 代碼二
簡要介紹
二分算法是我們寫算法題目中比較常見的一種優化算法,這個算法很好地體現了分治的思想,我們的二分算法不管是在算法題目中屢見不鮮,在實際工程當中也是十分熱門的一個算法,比如我們的數據庫索引、文件系統、甚至是我們遊戲AI的路徑規劃都或多或少地用到了我們的二分算法,在我們的算法題目中常見的幾種二分算法分別是二分答案、二分區間和二分浮點數。
二分答案
這是一個在有單調性的區間中找值的一個算法,通過二分思想來調整我們的查找範圍。
二分區間
這個其實和我們的二分答案類似,只不過這裏是搜索的一個區間而不是一個值,這種方法常應用於在區間內查找某一個解的情況。
二分浮點數
這個就比較冷門了,這裏其實和二分答案類似,只是這裏的處理方式不同而已。
相關例題
二分查找
題目描述
給定一個 n 個元素有序的(升序)整型數組 nums 和一個目標值 target ,寫一個函數搜索 nums 中的 target,如果 target 存在返回下標,否則返回 -1。
你必須編寫一個具有 O(log n) 時間複雜度的算法。
示例 1:
輸入: nums = [-1,0,3,5,9,12], target = 9
輸出: 4
解釋: 9 出現在 nums 中並且下標為 4示例 2:
輸入: nums = [-1,0,3,5,9,12], target = 2
輸出: -1
解釋: 2 不存在 nums 中因此返回 -1提示:
- 你可以假設
nums中的所有元素是不重複的。 n將在[1, 10000]之間。nums的每個元素都將在[-9999, 9999]之間。
題目分析
這個題目是一道相當經典的一道二分答案的題目,我們這裏的思想就是二分。
實現思路
定義兩個指針,一個左指針left,一個右指針right,分別指向我們的數組的左右端,計算出我們的中間點mid,然後就是三種情況的討論了:
1、arr[mid] == target説明找到了,直接返回即可。
2、arr[mid] > target説明我們的區間[mid, right]都是要大於我們的target的,所以我們要捨棄這個區間的值,在我們的左邊[left, mid - 1]繼續查找,也就是讓我們的right = mid - 1。
3、arr[mid] < target説明我們的區間[left, mid]這個區間的值都是要小於我們的target的,所以我們這裏要捨棄這一段區間,在我們的區間[mid + 1, right]繼續進行查找,也就是讓我們的left = mid + 1。
以上三個操作都是在while(left < right)條件下進行的,跳出循環説明沒有找到。
實現代碼
class Solution {
public:
int search(vector<int>& nums, int target) {
int n=nums.size();
int left=0,right=n-1;
while(left<=right)
{
int mid=left+(right-left+1)/2;
if(nums[mid]<target) left=mid+1;
else if(nums[mid]>target) right=mid-1;
else return mid;
}
return -1;
}
};在排序數組中查找元素的第一個和最後一個位置
題目描述
給你一個按照非遞減順序排列的整數數組 nums,和一個目標值 target。請你找出給定目標值在數組中的開始位置和結束位置。
如果數組中不存在目標值 target,返回 [-1, -1]。
你必須設計並實現時間複雜度為 O(log n) 的算法解決此問題。
示例 1:
輸入:nums = [5,7,7,8,8,10], target = 8
輸出:[3,4]示例 2:
輸入:nums = [5,7,7,8,8,10], target = 6
輸出:[-1,-1]示例 3:
輸入:nums = [], target = 0
輸出:[-1,-1]提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109nums是一個非遞減數組-109 <= target <= 109
題目分析
這個題目就是我們之前説的二分區間的經典例題,這裏其實還是比較容易混淆的,這裏我們做一個區分(使用基礎二分,通過基礎二分模板然後保留特定的左或是右下標的方式的做法其實是找到的值不一定是等於我們的target的,這裏的就是必須要是等於target的算法)。
實現思路
我們這裏的基本思路就是找到我們的左邊界和我們的右邊界,這是兩種不同的情況,我們這裏需要分開討論着兩種情況的:
找左邊界:
我們這裏需要明確幾個區間的特點:
我們的左區間[left, k - 1]都是要小於我們的target的。
我們的右區間[k, right]都是要大於等於我們的target的。
所以這裏我們的mid的位置右有了下面的兩種情況:
當我們的mid在[left, k - 1]的時候,也就是説arr[mid] < target,説明[left, mid]都是可以捨棄的,我們這裏和我們的二分答案的更新是一樣的就是將left移到mid + 1的位置上。
但是當我們這裏的mid在[k, right]的時候就和我們的二分答案的地方不一樣了,這裏我們是大於等於我的target值,我們要找的就是tatget值在的最左邊的下標,所以這裏的k我們是不能捨棄的,我們這裏可以將我的[left + 1, right]捨棄掉,所以這裏我們可以將right更新到mid位置。
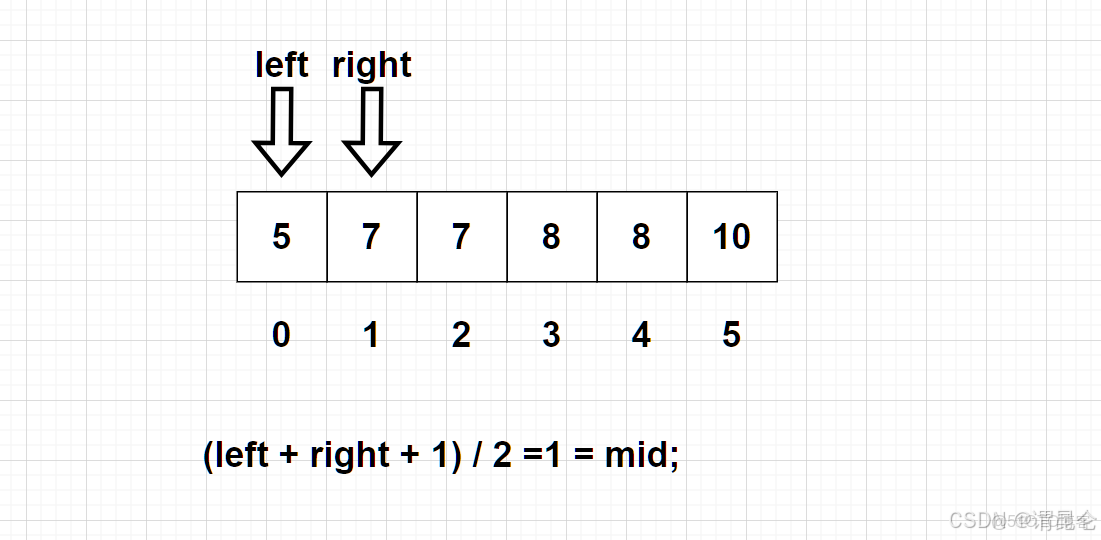
需要特別注意的是(也是特別容易出錯的):我們這裏一定是向下取整。
示例(如果是向上取整):
我們這裏圖示的情況就是陷入了死循環的狀態,所以這裏我們採取的應該是向下取整,這裏我們也是比較好理解的,相較於我們的二分答案我們這裏的代碼主要還是沒有讓我們的右指針往左靠,於是我們這裏採用向下調整整體上是使得我們的mid更加向我們的left靠近了,這也就彌補了右指針沒往左靠的問題。
我們這裏分析我們的右邊界也是一樣的,首先還是要明確我們的區間特點:
左區間
[left, k]都是要小於等於target的。右區間
[k + 1, right]都是要大於我們的target的。
我們的mid位置的情況也是兩種:
當我們的mid在[left, k]區間的時候,因為這個區間是小於等於我們的target的,所以這裏的mid是不能捨棄的,我們這裏可以將區間[left, mid - 1]捨棄,於是這裏的更新就變成了left = mid。
當我們的mid在[k + 1, right]的時候,説明我們的[mid, right]都是大於target的,所以這裏的區間內的值都是可以捨棄的,於是這裏的更新就變成了right = mid - 1。
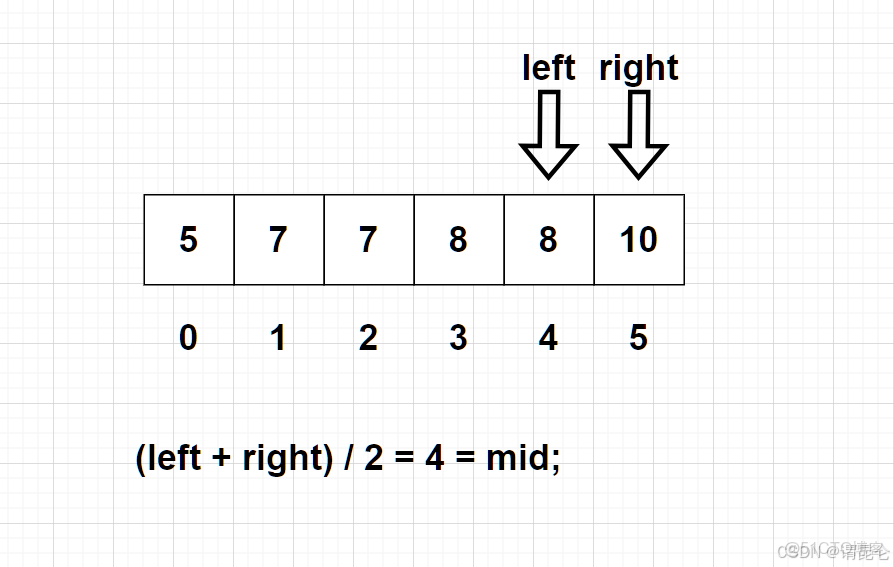
注意:我們這裏的區間是要向上取整的。
我們這裏還是舉出一個向下取整而導致死循環的例子:這裏的解釋和上面類似。
實現代碼
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int n=nums.size();
if(n==0) return {-1,-1};
int left=0,right=n-1;
while(left<right)
{
int mid=left+(right-left)/2;
if(nums[mid]<target) left=mid+1;
else right=mid;
}
int Left=0;
if(nums[left]!=target) return {-1,-1}; // 如果找到的下標對應的值不是目標值説明我們整個區間內都沒有這個target直接返回{-1, -1}即可
else Left=left;
left=0,right=n-1;
while(left<right)
{
int mid=left+(right-left+1)/2;
if(nums[mid]<=target) left=mid;
else right=mid-1;
}
return {Left,left};
}
};小技巧
這裏給一個取整的小技巧,while裏面有-1,我們的取整就要
+1,反之則沒有+1。
搜索插入位置
題目描述
給定一個排序數組和一個目標值,在數組中找到目標值,並返回其索引。如果目標值不存在於數組中,返回它將會被按順序插入的位置。
請必須使用時間複雜度為 O(log n) 的算法。
示例 1:
輸入: nums = [1,3,5,6], target = 5
輸出: 2示例 2:
輸入: nums = [1,3,5,6], target = 2
輸出: 1示例 3:
輸入: nums = [1,3,5,6], target = 7
輸出: 4提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums為 無重複元素 的 升序 排列數組-104 <= target <= 104
題目分析
這個題目實際上可以轉換成找出大於等於目標值的最左端,這樣我們就可以複用之前寫的代碼了。
實現思路
這裏的實現思路就是上面題目中的找左邊界的思路,不過這裏我們可以右兩種寫法,也是上面提到的容易混淆的情況,這裏我們其實可以使用二分的基礎模板,然後標記大於等於目標值的下標即可。
實現代碼
代碼一
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int ret=-1;
int left=0,right=nums.size()-1;
if(nums[nums.size()-1]<target) return nums.size();
while(left<right)
{
int mid=left+(right-left)/2;
if(nums[mid]<target) left=mid+1;
else right=mid;
}
return left;
}
};代碼二
class Solution {
public:
int searchInsert(vector<int>& a, int value) {
int L = 0;
int R = a.size() - 1;
if(a[a.size()-1]<value) return a.size();
int index = -1;
while(L <= R) {
int mid = L + ((R - L + 1)>>1);
if(a[mid] >= value) {
index = mid;
R = mid - 1;
}else {
L = mid + 1;
}
}
return index;
}
};x 的平方根
題目描述
給你一個非負整數 x ,計算並返回 x 的 算術平方根 。
由於返回類型是整數,結果只保留 整數部分 ,小數部分將被 捨去 。
**注意:**不允許使用任何內置指數函數和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
輸入:x = 4
輸出:2示例 2:
輸入:x = 8
輸出:2
解釋:8 的算術平方根是 2.82842..., 由於返回類型是整數,小數部分將被捨去。提示:
0 <= x <= 231 - 1
題目分析
我們這個題目其實也是可以轉換一下,我們這裏實際求的是小於等於根號x的最大值,於是這裏我們也是可以複用我們第二題的代碼的,當然了,這裏也是可以複用第三題的代碼二的。
實現思路
其實這裏就是條件改變了一下,基本的思路和之前還是一模一樣的,這裏就不再贅述了。
實現代碼
代碼一
class Solution {
public:
int mySqrt(int x) {
int left=1,right=x;
if(x<1) return 0; // 邊界情況
while(left<right)
{
long long mid=left+(right-left+1)/2;
if(mid*mid<=x) left=mid;
else right=mid-1;
}
return left;
}
};代碼二
class Solution {
public:
int mySqrt(int x) {
int left=1,right=x;
if(x<1) return 0; // 邊界情況
int index = -1;
while(left <= right)
{
long long mid=left+(right-left+1)/2;
if(mid*mid<=x) {
index = mid;
left = mid + 1;
}
else right=mid-1;
}
return index;
}
};