本篇文章主要進行算法練習題講解
1 串聯所有單詞的子串
鏈接:https://leetcode.cn/problems/substring-with-concatenation-of-all-words/description/
題目描述:
給定一個字符串
s和一個字符串數組words。words中所有字符串 長度相同。
s中的 串聯子串 是指一個包含words中所有字符串以任意順序排列連接起來的子串。
- 例如,如果
words = ["ab","cd","ef"], 那麼"abcdef","abefcd","cdabef","cdefab","efabcd", 和"efcdab"都是串聯子串。"acdbef"不是串聯子串,因為他不是任何words排列的連接。返回所有串聯子串在
s中的開始索引。你可以以 任意順序 返回答案。
示例 1:
[0,9]
示例 2:
輸出:[]
示例 3:
輸入:s = "barfoofoobarthefoobarman", words = ["bar","foo","the"] 輸出:[6,9,12] 解釋:因為 words.length == 3 並且 words[i].length == 3,所以串聯子串的長度必須為 9。 子串 "foobarthe" 開始位置是 6。它是 words 中以 ["foo","bar","the"] 順序排列的連接。 子串 "barthefoo" 開始位置是 9。它是 words 中以 ["bar","the","foo"] 順序排列的連接。 子串 "thefoobar" 開始位置是 12。它是 words 中以 ["the","foo","bar"] 順序排列的連接。
提示:
1 <= s.length <= 1041 <= words.length <= 50001 <= words[i].length <= 30words[i]和s由小寫英文字母組成
題目解析:
這道題目會給你一個字符串 s 和一個字符串數組 words,其中 words 中每一個字符串的長度都是相同的。這道題目是讓你在 s 中找出所有 words 的串聯子串的起始索引,其中串聯子串是指由 words 中所有字符串任意組合而成的一個新的字符串,比如 words = ["ab", "cd", "ef"],那麼 "abcdef"、"abefcd"、"cdabef"、"cdefab"、"efabcd"、"efcdab" 都是其串聯子串。例如:s = "ababcdefcdab",words = ["ab", "cd", "ef"],返回 vector<int> = [2, 6]
算法講解:
這道題目其實與我們之前做過的一到題目 -- 找出字符串中的所有字母異位詞很像,那道題是在一個字符串 s 中找到另一個字符串 p 的所有字母異位詞,異位詞就是 p 字符串的所有字符隨機組合而形成的字符串,這道題目由於 words 中每個字符串長度是一樣的,如果我們將 words 中每一個字符串看成是字母 a, b, c,s 中每 words[0].size() 個字符看成是一個字符,那麼這道題就變成了找出字符串中的所有字母異位詞題目了。比如示例1:s = "barfoothefoobarman",words = ["foo", "bar"],我們將 words 看成 words = ['a', 'b'],那麼 s = "bacabd",這就變成了上面的那一道題目。
哈希表 + 滑動窗口算法的解法,只不過與那一道題目有所區別:
(1) 哈希表的形式:之前那道題目因為是字符,我們用的是一個整數數組來作為哈希表統計有效字符的出現次數;但是這裏是字符串,我們需要用到 STL 中的一個容器,那就是 unordered_map<string, int> 作為哈希表來統計有效字符串出現的次數(如果這個容器沒學過,可以先跳過,後面學過了之後再做)。
(2) left 與 right 的移動:這裏顯然每次要移動 words 中一個字符串的長度,因為這裏是將一個字符串作為一個單位移動的
(3) 滑動窗口執行的次數:這裏滑動窗口應該執行 words 中每一個字符串的長度次,比如:s = "afoobarabcfoo", words = ["foo", "bar"],所以起始位置也可能從索引1開始;再比如:s = "abfoobarabcef", words = ["foo", bar],起始位置也可能從索引 2 開始,但是再往後,如果從索引 3 開始,其實是與從索引 0 開始是一樣的,只不過多一個單詞而已。
代碼:
class Solution
{
public:
vector findSubstring(string s, vector& words)
{
vector v;
//首先利用 hash1 統計 words 中每個字符串出現的次數
unordered_map hash1;
for (auto& str : words)
hash1[str]++;
int len = words[0].size();
//開始滑動窗口
//要進行 len 次
for (int i = 0; i < len; i++)
{
unordered_map hash2;//利用 hash2 統計 s 字符串中子串的長度
int left = i, right = i;
int count = 0;//統計有效字符串數
while (right + len <= s.size())
{
//進窗口
string in = s.substr(right, len);
hash2[in]++;
if (hash1[in] >= hash2[in]) ++count;
//判斷
while (right - left + 1 > words.size() * len)
{
//出窗口
string out = s.substr(left, len);
if (hash1[out] >= hash2[out]) --count;
hash2[out]--;
left += len;
}
//更新結果
if (count == words.size()) v.push_back(left);
right += len;
}
}
return v;
}
};,>,>2 最小覆蓋子串
鏈接:https://leetcode.cn/problems/M1oyTv/
題目描述:
給定兩個字符串
s和t。返回s中包含t的所有字符的最短子字符串。如果s中不存在符合條件的子字符串,則返回空字符串""。如果
s中存在多個符合條件的子字符串,返回任意一個。
注意: 對於
t中重複字符,我們尋找的子字符串中該字符數量必須不少於t中該字符數量。
示例 1:
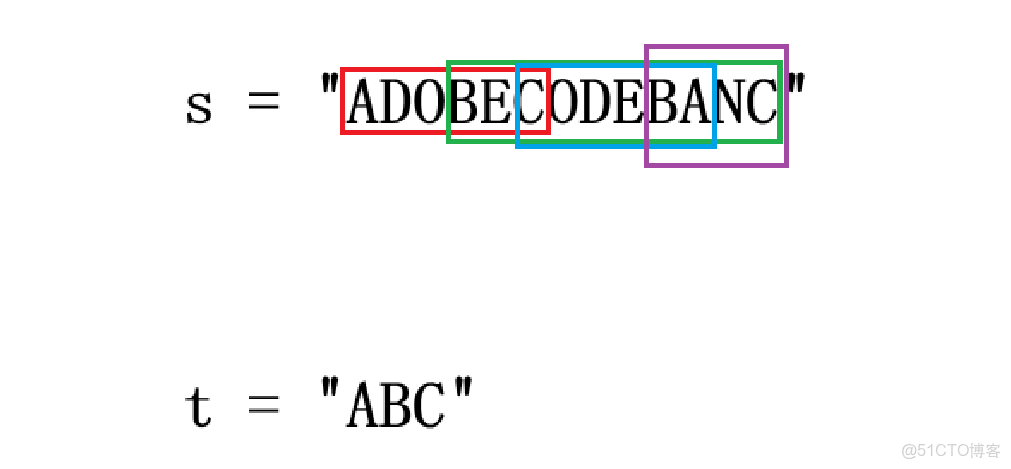
輸入:s = "ADOBECODEBANC", t = "ABC" 輸出:"BANC" 解釋:最短子字符串 "BANC" 包含了字符串 t 的所有字符 'A'、'B'、'C'
示例 2:
輸入:s = "a", t = "a" 輸出:"a"
示例 3:
輸入:s = "a", t = "aa" 輸出:"" 解釋:t 中兩個字符 'a' 均應包含在 s 的子串中,因此沒有符合條件的子字符串,返回空字符串。
提示:
1 <= s.length, t.length <= 105s和t由英文字母組成
題目解析:
這道題目會給你一個 s 字符串與 t 字符串,該題目要求你返回 s 字符串中包含了 t 字符串中所有字符的最短子串(t 中如果存在兩個相同字符,那也算是兩個字符),其中這個子串包含的 t 字符串中字符的個數可以多於 t 字符串中的字符個數,但是不是少於 t 字符串中的字符個數。比如:
s 中滿足條件的子串如圖所示,顯然最短的子串就是 "BANC",所以返回的字符串就是 "BANC"
算法講解:
我們可以先利用暴力解法來解決問題:我們可以從第一個字符開始,然後依次向後找,直到該子串滿足條件,我們就可以停止向後尋找;然後再從第二個字符開始,重複該過程,知道枚舉到 s.size() - t.size() 位置,然後找到最短的子串就可以了,最後返回該子串,其中判斷子串是否滿足條件,我們依舊採用哈希表來記錄字符出現的次數:
class Solution
{
public:
string minWindow(string s, string t)
{
if (s.size() < t.size()) return "";
//先利用 hash1 來記錄 t 中字符串出現的次數
int hash1[128] = { 0 };
for (auto& ch : t) hash1[ch]++;
int start = 0, len = INT_MAX;//記錄開始位置與長度
for (int i = 0; i <= s.size() - t.size(); i++)
{
//i 作為子串的左端點
int j = i;
int count = 0;//count 用來記錄滿足條件的字符數
int hash2[128] = { 0 };//hash2 來記錄出現的字符數
while (j < s.size())
{
//j 作為子串的右端點
hash2[s[j]]++;
if (hash1[s[j]] >= hash2[s[j]]) ++count;
if (count == t.size()) break;
++j;
}
if (count == t.size())
if (j - i + 1 < len)
{
start = i;
len = j - i + 1;
}
}
if (len == INT_MAX) return "";
else return s.substr(start, len);
}
};顯然,該算法的時間複雜度為 O(n^2)。
滑動窗口的算法來解決問題:
(1) 定義 left = 0, right = 0, hash1[128] = { 0 }, hash2[128] = { 0 },hash1 用來記錄 t 中有效字符的個數,hash2 用來記錄 s 中有效字符的個數,count = 0,count 用來記錄有效字符的個數
(2) 進窗口:hash2[s[right]]++,如果 hash1[s[right]] >= hash1[s[right]],++count
(3) 判斷:這裏的判斷比較難想,在暴力解法中,當 j 走到滿足條件的位置時,我們才會停止枚舉,所以我們這裏的判斷,就是當 [left, right] 的子串滿足條件時,也就是 count == t.size() 時,才會出窗口,出窗口也很簡單,如果 hash1[s[left]] >= hash2[s[left]],那就讓 count--,再讓hash2[s[]left]--,然後 ++left
(4) 更新結果:由於是在滿足條件時出窗口,所以我們更新結果是在判斷裏面進行的,由於更新結果是更新一個起始位置和一個子串的長度,所以在準備階段還需要定義一個 start 與 len 來更新結果
代碼:
class Solution
{
public:
string minWindow(string s, string t)
{
if (s.size() < t.size()) return "";
//先利用 hash1 來記錄 t 中字符串出現的次數
int hash1[128] = { 0 };
for (auto& ch : t) hash1[ch]++;
int start = 0, len = INT_MAX;//記錄開始位置與長度
int left = 0, right = 0, count = 0;
int hash2[128] = { 0 };//hash2 記錄 s 子串中字符出現次數
while (right < s.size())
{
//進窗口
hash2[s[right]]++;
if (hash1[s[right]] >= hash2[s[right]]) ++count;
//判斷
while (count >= t.size())
{
//更新結果
if (right - left + 1 < len)
{
len = right - left + 1;
start = left;
}
//出窗口
if (hash1[s[left]] >= hash2[s[left]]) --count;
hash2[s[left]]--;
++left;
}
++right;
}
return len == INT_MAX ? "" : s.substr(start, len);
}
};3 最接近的三數之和
鏈接:16. 最接近的三數之和 - 力扣(LeetCode)
題目描述:
給你一個長度為
n的整數數組nums和 一個目標值target。請你從nums中選出三個整數,使它們的和與target最接近。返回這三個數的和。
假定每組輸入只存在恰好一個解。
示例 1:
輸入:nums = [-1,2,1,-4], target = 1 輸出:2 解釋:與 target 最接近的和是 2 (-1 + 2 + 1 = 2)。
示例 2:
輸入:nums = [0,0,0], target = 1 輸出:0 解釋:與 target 最接近的和是 0(0 + 0 + 0 = 0)。
提示:
3 <= nums.length <= 1000-1000 <= nums[i] <= 1000-104 <= target <= 104
題目解析:
這道題目與三數之和很像,只不過這個題目是尋找 nums 數組中三個數字和與 target 最接近的三個數字,並且返回這三個數字的和。比如:nums = [-1, 2, 1, 4],target = 1,那麼返回的就是2,因為加起來和與 1 最接近的三個數字就是[-1, 1, 2],所以最終返回的結果就是這三個數字的和 2。
算法講解:
排序 + 雙指針。首先我們會先對數組進行排序,然後我們固定第一個數 nums[i],然後在剩下的區間[i + 1, nums.size() - 1]中選擇兩個數字 nums[left] 與 nums[right],如果三個數字的和正好等於 target,那麼這這三個數字就是最優解,因為每組輸入中僅存在一個解,所以直接返回 target 就可以了;當 nums[i] + nums[left] + nums[right] > target 時,説明是三個數字大了,那麼我們就 --right;如果 nums[i] + nums[left] + nums[right] < target,此時説明三個數字小了,那麼我們就 ++left,但是這道題目有一個特殊點,那就是找最接近的,我們需要尋找一種方法來更新最優解。
與 target 最接近的數字是用與 target 的距離來表示的,兩個數字之間的距離在數學上是用絕對值來衡量的,所以我們這裏採用絕對值來更新結果。比如:target = 8,而一個 sum = 7,另一個 sum = 10(這裏的 sum 代表 nums[i] + nums[left] + nums[right]),很顯然 7 更接近 target,因為 abs(7 - 8) < abs(10 - 8)(abs 是求絕對值的庫函數包含在 math.h 頭文件下),所以在雙指針在尋找兩個數字的過程中,我們採用絕對值來更新結果:如果 abs(sum - target) < abs(best - target),我們更新 best = sum,其中 best 記錄最優解。
當然這道題目也可以優化一點時間複雜度,就是跳過相同元素,這裏就不再優化了,感興趣可以自己寫一下。
代碼:
class Solution
{
public:
int threeSumClosest(vector& nums, int target)
{
sort(nums.begin(), nums.end());
long long best = INT_MAX;
//固定第一個數字
for (int i = 0; i < nums.size() - 2; ++i)
{
int a = nums[i];
int left = i + 1, right = nums.size() - 1;
while (left < right)
{
int b = nums[left], c = nums[right];
long long sum = a + b + c;
if (sum == target) return target;
if (abs(sum - target) < abs(best - target)) best = sum;
if (a + b + c < target) ++left;
else --right;
}
}
return best;
}
};