實用指南：AVL樹的實現詳情 - 子節點,父節點,子樹,HarmonyOS,後端開發 mb61c46a7ab1eee 博客

AVL樹的概念

要理解AVL 樹，首先要了解二叉搜索樹，關於二叉搜索樹是什麼，可以參考下面這篇：

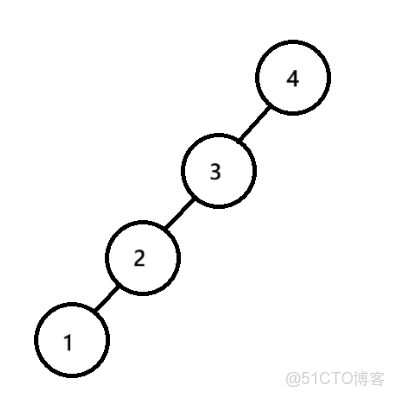
一般情況下，二叉搜索樹的時間複雜度是O（log n）但是在極端情況下會退化為單支樹，時間複雜度退化為O(N)

實用指南：AVL樹的實現_子樹

為了避免效率下降，因此AVL樹被髮明出來了

1.性質

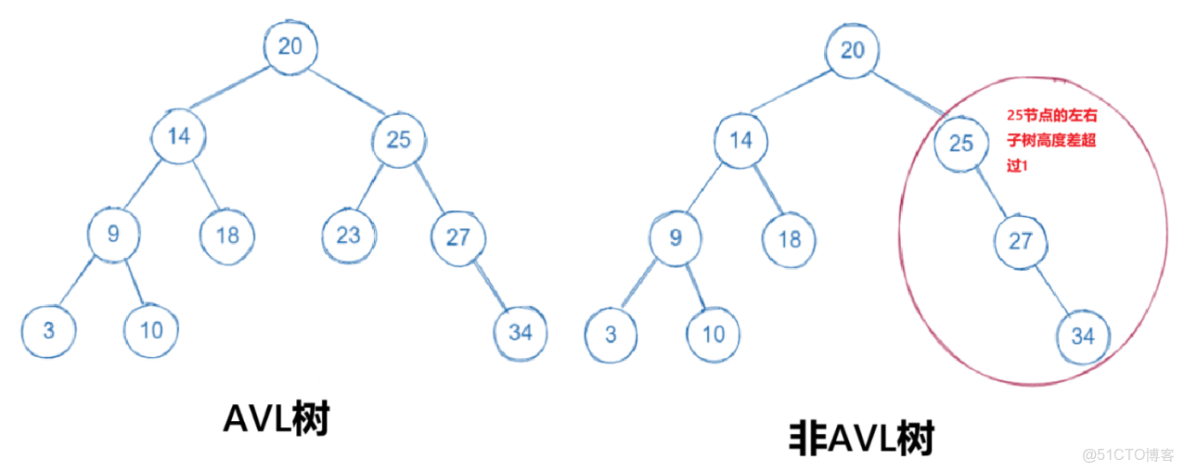
AVL樹的左右子樹高度差不超過1
AVL樹的左右子樹也是AVL樹
AVL樹可以為空樹

實用指南：AVL樹的實現_父節點_02

2.AVL樹的定義

AVL樹的左右子樹高度差不能超過1，這裏為了方便講解，引入平衡因子（_bf)這個概念，

平衡因子==該節點右子樹高度-該節點左子樹的高度，例如：

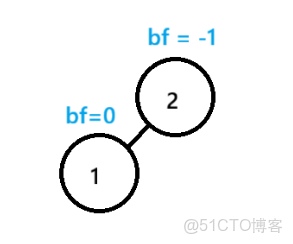
實用指南：AVL樹的實現_子樹_03

節點1左右子樹高度都為0，平衡因子 = 右高度-左高度：bf = 0 - 0

節點2左子樹高度為1，右子樹為0，平衡因子 = 0 - 1

如果平衡因子的大小超過1，AVL樹的規則被打破，需要調整從而達到平衡

在調整的過程中會頻繁的使用到父節點，因此AVL樹的每個節點要有三個指針，左右子節點的指針、父指針

為了方便講解，這裏使用value模型的AVL樹，即：節點只包含一個數據，並非常見的key-value鍵值對

template
struct AVLTreeNode
{
	AVLTreeNode(const T& data = T())
		: _pLeft(nullptr)
		, _pRight(nullptr)
		, _pParent(nullptr)
		, _data(data)
		, _bf(0)
	{}
	AVLTreeNode* _pLeft;
	AVLTreeNode* _pRight;
	AVLTreeNode* _pParent;
	T _data;
	int _bf;   // 節點的平衡因子
};

3.AVL樹的插入

往AVL樹中插入節點與二叉搜索樹中插入節點的過程基本相同，需要一個一個插入，區別是AVL樹的插入要調整平衡因子

插入數據的總體思路為：判斷根節點是否為空，尋找插入位置，完善插入的節點與周圍節點的指向，向上調整平衡因子

1.往空樹中插入一個值，直接將-pRoot指向該節點就可以了

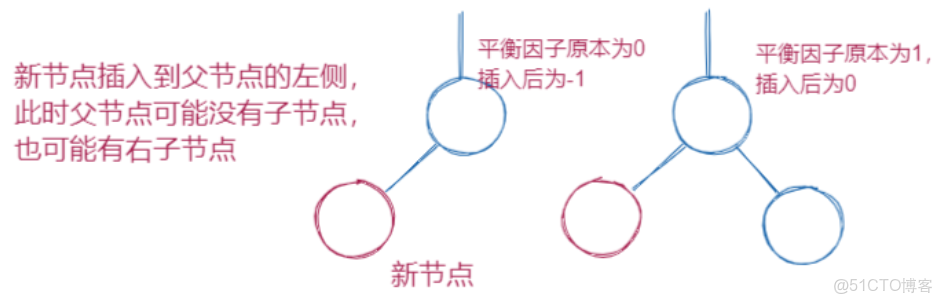
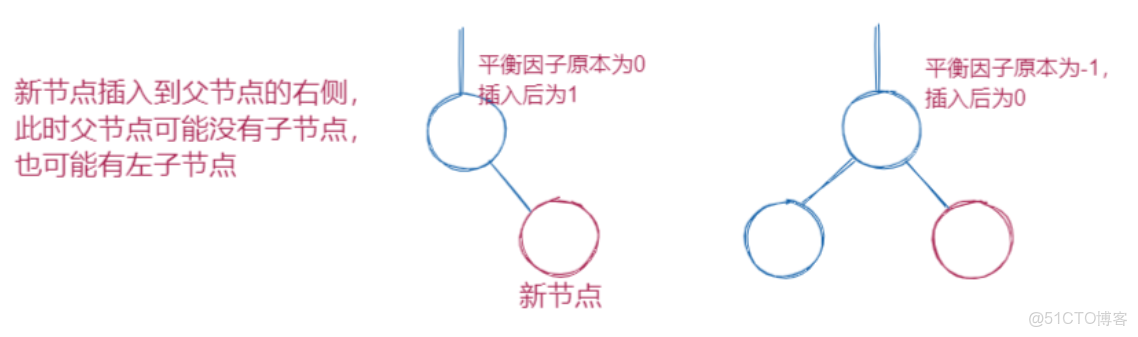
2.往一個節點的左子樹插入一個節點，該節點的bf要-1

實用指南：AVL樹的實現_父節點_04

3.往一個節點的右子樹插入一個節點，該節點的bf要+1

實用指南：AVL樹的實現_子節點_05

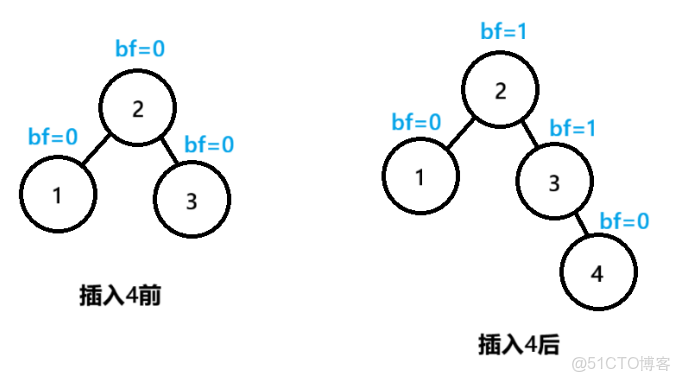
插入一個值後，在沒有旋轉的情況下，bf值為1或者-1，原先的bf值必然為0，意味着該節點的左右子樹的高度發生了變化，此時需要繼續向上修正祖先節點的bf值，直到根節點，或者其中有某個節點的bf值變為0（因為節點是一個一個插入的，每插入一個都要向上調整bf值，一旦有節點在調整bf值的過程中，bf變為0，一定是從-1或者1變過來的，此時該節點的左右子樹高度不變，無需向上調整）如圖：

實用指南：AVL樹的實現_父節點_06

觀察上圖：

在插入4之後，3節點的bf=1，3節點所在的樹的高度發生變化，還需要向上調整

2節點的bf=1，到達根節點，調整結束

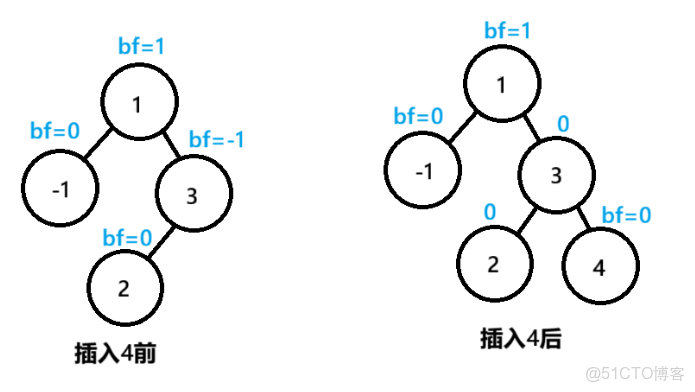
實用指南：AVL樹的實現_父節點_07

觀察上圖，在插入4這個節點後，3的bf值由原來的-1變成了0

3節點所在的樹的高度不變，此時無需再向上調整，1節點的bf仍然為1

可以總結出規律：在調整平衡因子過程中，如果得到bf=1或者bf=-1，此樹的高度發生了變化，需要繼續向上調整；得到bf=0，此樹的高度不變，無需向上調整

// 在AVL樹中插入值為data的節點
bool Insert(const T& data)
{
	//根節點為空
	if (_pRoot == nullptr)
	{
		_pRoot = new Node(data);
		return true;
	}
	else
	{
		//根節點不為空
		Node* cur = _pRoot;
		Node* parent = nullptr;
		//尋找插入位置
		while (cur)
		{
			if (data < cur->_data)
			{
				parent = cur;
				cur = cur->_pLeft;
			}
			else if (data > cur->_data)
			{
				parent = cur;
				cur = cur->_pRight;
			}
			else
			{
				cout << "數據冗餘，插入" << data << "失敗" << endl;
				return false;
			}
		}
		//找到了插入位置,插入
		cur = new Node(data);
		if (data < parent->_data)
		{
			parent->_pLeft = cur;
		}
		else
		{
			parent->_pRight = cur;
		}
		cur->_pParent = parent;
		//修正平衡因子
		while (parent)
		{
			if (cur == parent->_pLeft)
			{
				parent->_bf--;
			}
			else
			{
				parent->_bf++;
			}
			if (parent->_bf == 0)
			{
				//無需向上調整
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1)
			{
				//繼續向上調整
				cur = parent;
				parent = parent->_pParent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				//
			}
			else
			{
				cout << "AVL樹高度異常" << endl;
				assert(false);
			}
		}
	}
}

插入會有失衡的情況，即_bf的值達到了2或者-2，此時樹的結構被破話，會涉及四種旋轉：右旋、左旋、右左雙旋、左右雙旋，如何旋轉呢？

4.AVL樹的旋轉

AVL樹的旋轉大體上有4種，這裏會詳細講解這四種旋轉：右單旋、左單旋、右左雙旋、左右雙旋

當一個節點的左右高度差為2時，即bf=2或者bf=-2，此時需要通過旋轉進行調整，讓該樹滿足AVL的規則

旋轉採取的是使用最少或最簡單的步驟，使得這顆二叉樹的結構重新迴歸到AVL樹

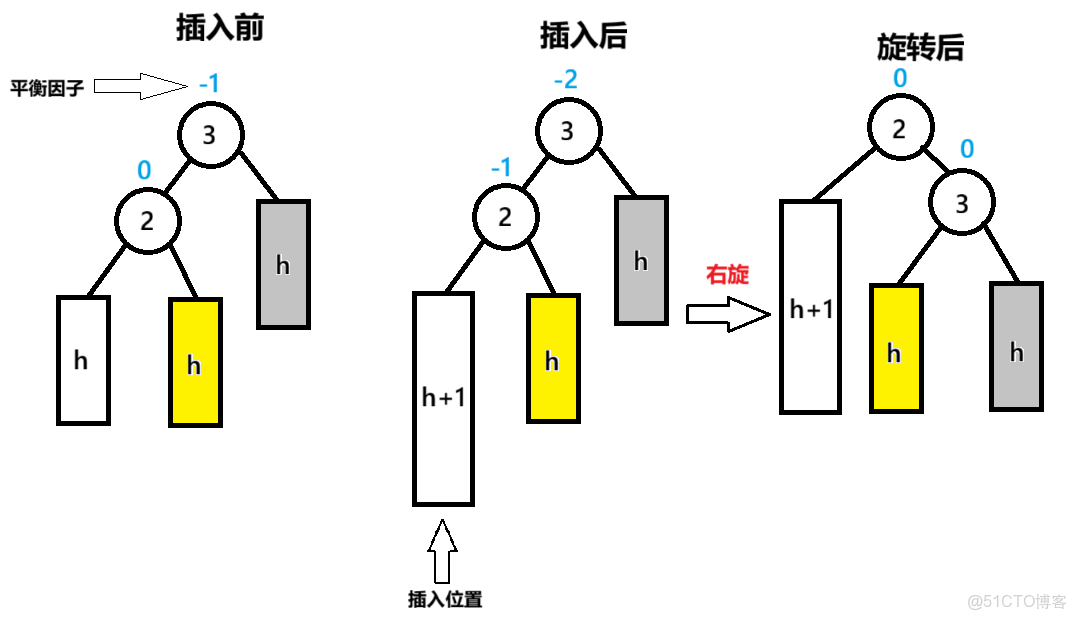
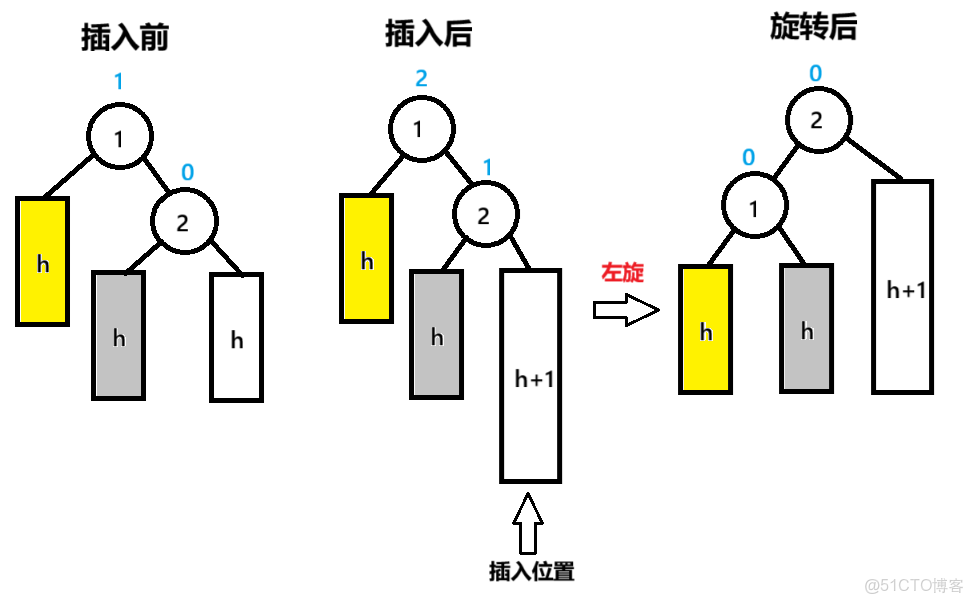
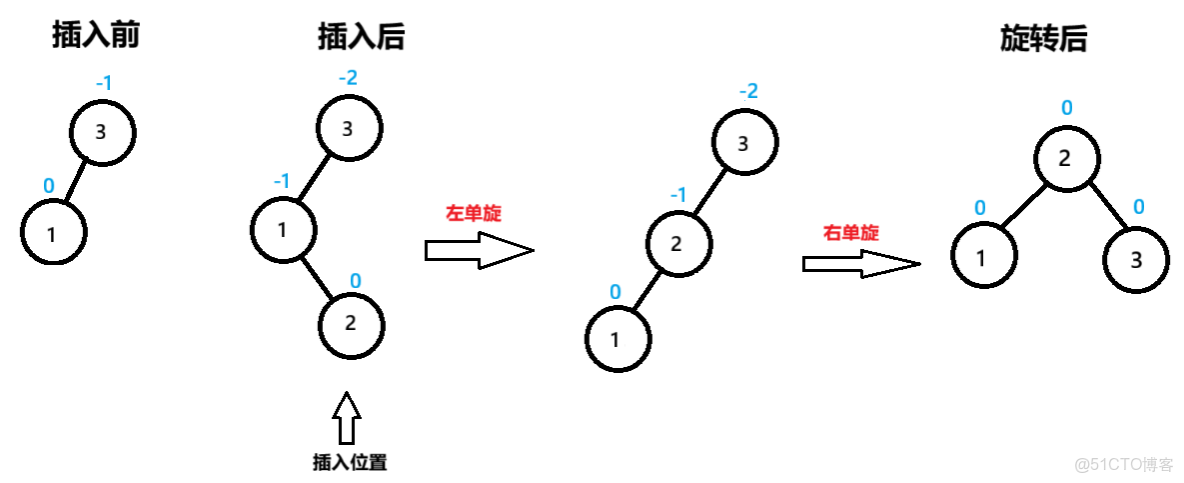
1.右單旋

旋轉是在插入後，修正平衡因子時候進行的

在修正過程中，子節點bf=-1，父節點bf=-2時，發生右單旋

實用指南：AVL樹的實現_子節點_08

節點3為pParent，節點2為NodeL，節點2的右子節點為NodeLR

以pParent為旋轉點，旋轉後，pParent（3節點）的bf=0

子節點（2節點）的bf=0

注意，這裏父子節點的定義是在旋轉前確定的

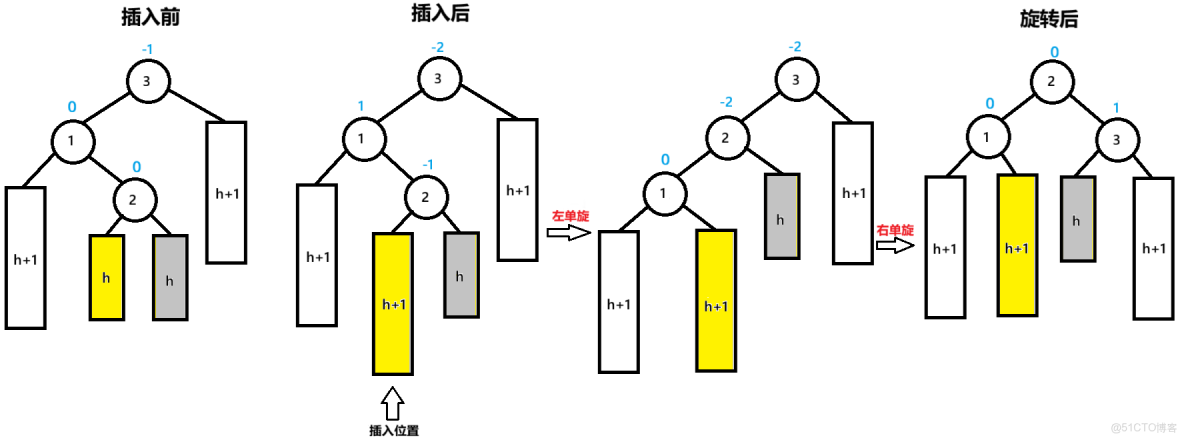
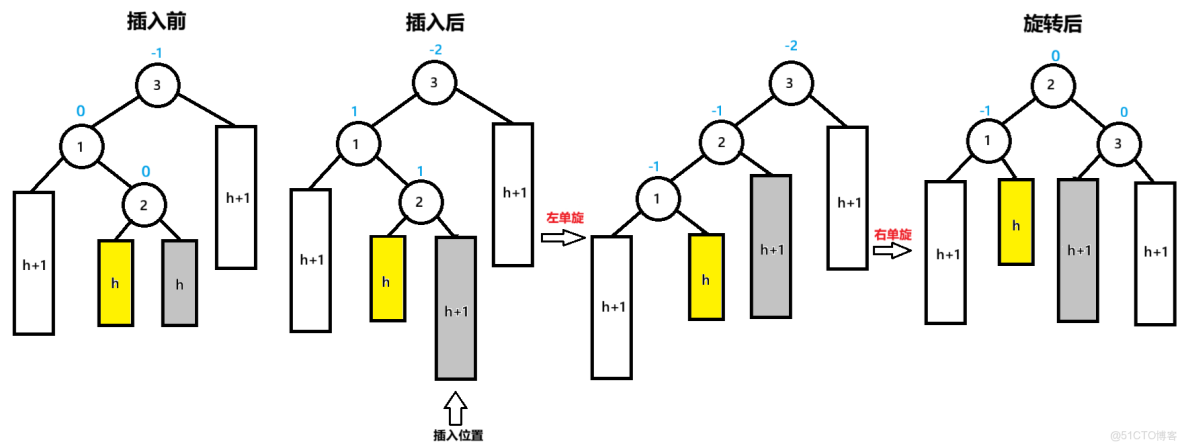
高度h的樹，高度在0、1、2等正數情況下都適用

這裏解釋一下2節點的右子樹在旋轉後為什麼變成了3節點的左子樹

首先，一個節點只有一個右節點的指針，這樣才符合二叉樹的規則

其次，以2節點為根的樹的節點，都小於3節點，因為2節點是3節點的左子節點

左子節點 < 根節點 < 右子節點

因此2的右子樹變成3的左子樹符合規則，而且是比較方便的處理方法

// 右單旋
void RotateR(Node* pParent)
{
	Node* NodeL = pParent->_pLeft;
	Node* NodeLR = NodeL->_pRight;
	Node* pParentParent = pParent->_pParent;
	//修正向下關係
	pParent->_pLeft = NodeLR;
	NodeL->_pRight = pParent;
	//修正向上關係
	pParent->_pParent = NodeL;
	if (NodeLR)
	{
		NodeLR->_pParent = pParent;
	}
	//修正外部關係
	if (pParentParent == nullptr)
	{
		_pRoot = NodeL;
		NodeL->_pParent = nullptr;
	}
	else
	{
		if (pParentParent->_pLeft == pParent)
		{
			pParentParent->_pLeft = NodeL;
		}
		else
		{
			pParentParent->_pRight = NodeL;
		}
		NodeL->_pParent = pParentParent;
	}
	//修正平衡因子
	pParent->_bf = 0;
	NodeL->_bf = 0;
}

注意：旋轉後要修正平衡因子，且此時的節點關係發生了變化需要格外小心

與插入後的修正平衡因子不是同一件事

2.左單旋

插入後的子節點bf=1，父節點bf=2時，發生左單旋

實用指南：AVL樹的實現_父節點_09

節點的確定在插入後，節點1為pParent，節點2為NodeR，節點2的左子節點為NodeRL

// 左單旋
void RotateL(Node* pParent)
{
	Node* NodeR = pParent->_pRight;
	Node* NodeRL = NodeR->_pLeft;
	Node* pParentParent = pParent->_pParent;
	//修正向下關係
	pParent->_pRight = NodeRL;
	NodeR->_pLeft = pParent;
	//修正向上關係
	pParent->_pParent = NodeR;
	if (NodeRL)
	{
		NodeRL->_pParent = pParent;
	}
	//修正外部關係
	if (pParentParent == nullptr)
	{
		_pRoot = NodeR;
		NodeR->_pParent = nullptr;
	}
	else
	{
		if (pParentParent->_pLeft == pParent)
		{
			pParentParent->_pLeft = NodeR;
		}
		else
		{
			pParentParent->_pRight = NodeR;
		}
		NodeR->_pParent = pParentParent;
	}
	//修正平衡因子
	NodeR->_bf = 0;
	pParent->_bf = 0;
}

左單旋與右單旋類似，相當於右單旋的左右鏡像版本，旋轉後的父子節點bf都為0

以節點2（）為旋轉點進行左單旋

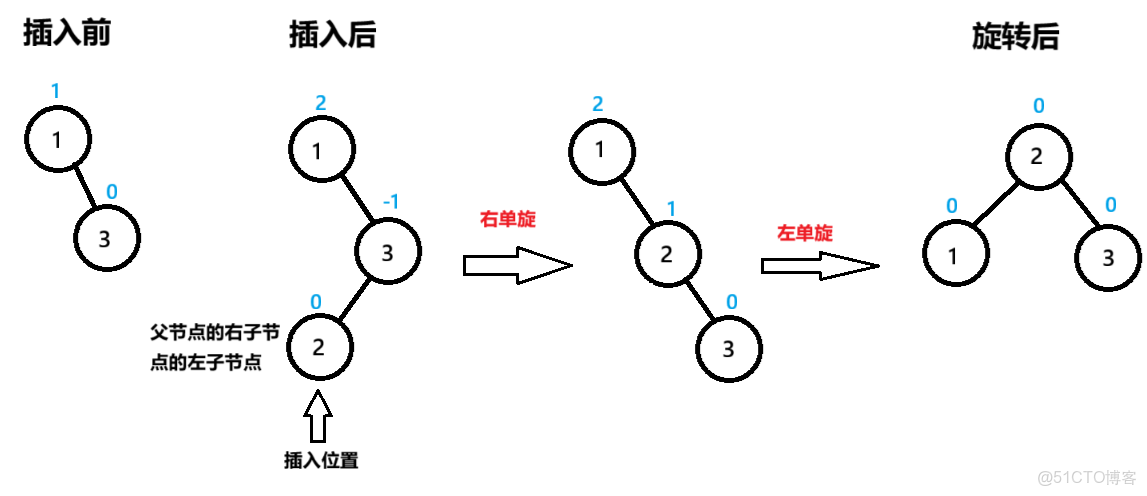
3.右左雙旋

雙旋是在單次旋轉無法達到平衡時出現的，本質上是兩次單旋，可以複用單旋的代碼

右左雙旋細分為3種情況，3種情況的共同點是在父節點bf=2

一：父節點bf=2，父節點的右子節點的左子節點bf=0

實用指南：AVL樹的實現_子節點_10

節點1為pParent，節點3為NodeR，節點2為NodeRL

先以節點NodeR為旋轉點進行右單旋，節點1的bf=2，未達到平衡

再以節點pParent為旋轉點進行左單旋

旋轉後的三個節點達到平衡，平衡因子都是0，bf=0

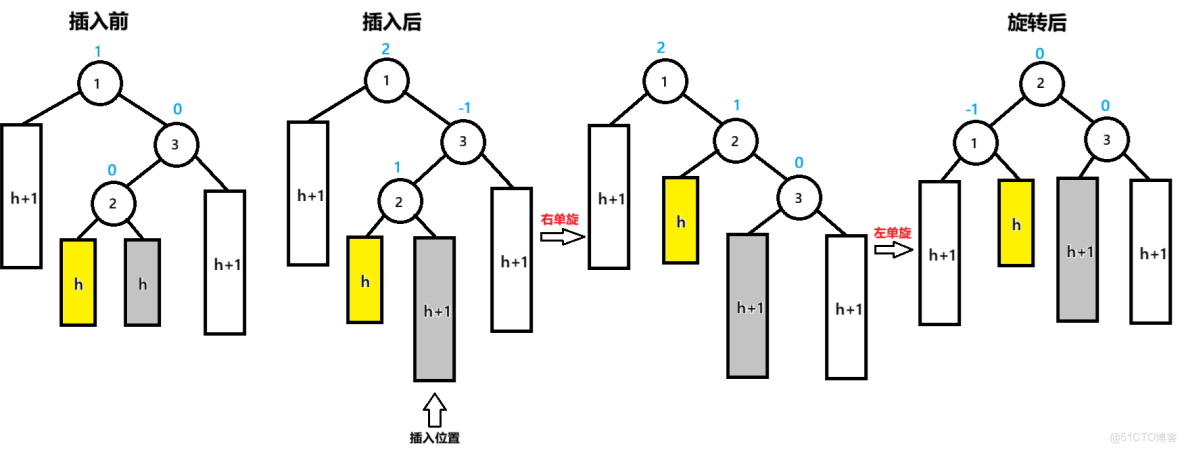
二：父節點bf=2，父節點的右子節點的左子節點bf=1

實用指南：AVL樹的實現_父節點_11

插入後，節點1為pParent，節點3為NodeR，節點2為NodeRL

先以節點NodeR為旋轉點進行右單旋，節點1的bf=2，未達到平衡

再以節點pParent為旋轉點進行左單旋，達到平衡

pParent的bf=-1，NodeR的bf=0，NodeRL的bf=0

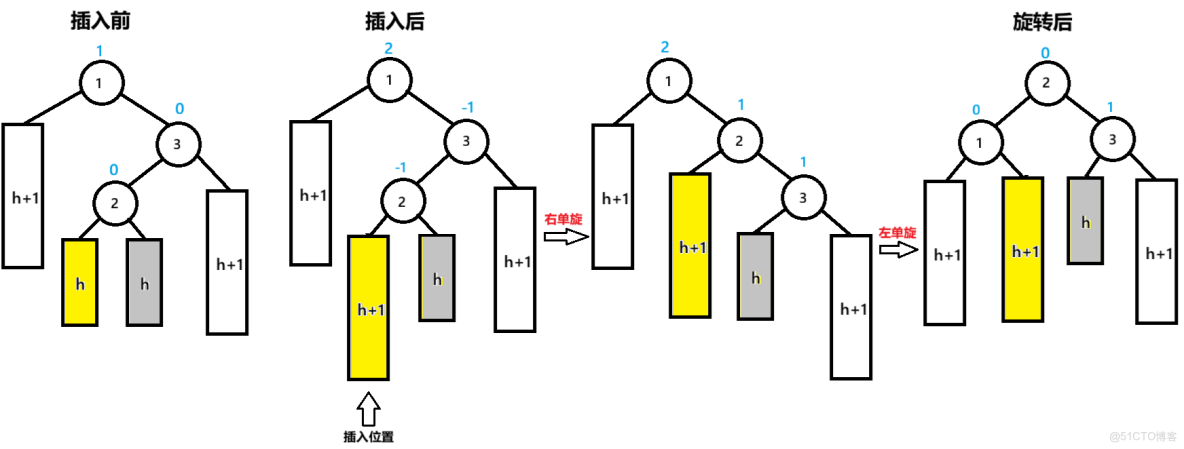
三：父節點bf=2，父節點的右子節點的左子節點bf=-1

實用指南：AVL樹的實現_父節點_12

插入後，節點1為pParent節點，節點3為NodeR，節點2為NodeRL

先以NodeR為旋轉點進行右單旋，pParent的bf=2，未達到平衡

再以pParent為旋轉點進行左單旋，達到平衡

pParent的bf=0，NodeR的bf= 1，NodeRL的bf=0

右左雙旋都是先進行右單旋，再進行左單旋得到的，不同點在於平衡因子

這三種情況的代碼可以複用，甚至複用單旋的代碼

// 右左雙旋
void RotateRL(Node* pParent)
{
	Node* NodeR = pParent->_pRight;
	Node* NodeRL = NodeR->_pLeft;
	int bf = NodeRL->_bf;
	RotateR(NodeR);
	RotateL(pParent);
	//校正平衡因子
	if (bf == 0)
	{
		pParent->_bf = 0;
		NodeR->_bf = 0;
		NodeRL->_bf = 0;
	}
	else if (bf == 1)
	{
		pParent->_bf = -1;
		NodeR->_bf = 0;
		NodeRL->_bf = 0;
	}
	else if (bf == -1)
	{
		pParent->_bf = 0;
		NodeR->_bf = 1;
		NodeRL->_bf = 0;
	}
	else
	{
		assert(false);
	}
}

4.左右雙旋

左右雙旋其實就是右左雙旋的左右鏡像版本

所以也有3種情況，這三種情況的不同也是因為bf的處理不同

一：父節點的bf=-2，父節點的左子節點的右子節點bf=0

實用指南：AVL樹的實現_子樹_13

節點3為pParent，節點1為NodeL，節點2為NodeLR

先以節點NodeL為旋轉點進行左單旋，節點3的bf=-2，未達到平衡

再以節點pParent為旋轉點進行右單旋

旋轉後的三個節點達到平衡，平衡因子都是0，bf=0

二：父節點的bf=-2，父節點的左子節點的右子節點bf=-1

實用指南：AVL樹的實現_子樹_14

插入後，節點3為pParent，節點1為NodeL，節點2為NodeLR

先以節點NodeL為旋轉點進行左單旋，節點3的bf=-2，未達到平衡

再以節點pParent為旋轉點進行右單旋，達到平衡

pParent的bf=1，NodeL的bf=0，NodeLR的bf=0

三：父節點的bf=-2，父節點的左子節點的右子節點bf=1

實用指南：AVL樹的實現_父節點_15

插入後，節點3為pParent，節點1為NodeL，節點2為NodeLR

先以節點NodeL為旋轉點進行左單旋，節點3的bf=-2，未達到平衡

再以節點pParent為旋轉點進行右單旋，達到平衡

pParent的bf=0，NodeL的bf=-1，NodeLR的bf=0

5.AVL樹的刪除

這部分比較困難，不作講解，請參考其他文獻

源碼：

包含測試用例以及打印函數，可直接執行

#include
#include
using namespace std;
template
struct AVLTreeNode
{
	AVLTreeNode(const T& data = T())
		: _pLeft(nullptr)
		, _pRight(nullptr)
		, _pParent(nullptr)
		, _data(data)
		, _bf(0)
	{}
	AVLTreeNode* _pLeft;
	AVLTreeNode* _pRight;
	AVLTreeNode* _pParent;
	T _data;
	int _bf;   // 節點的平衡因子
};
// AVL: 二叉搜索樹 + 平衡因子的限制
template
class AVLTree
{
	typedef AVLTreeNode Node;
public:
	AVLTree()
		: _pRoot(nullptr)
	{}
	void Display()
	{
		_Display(_pRoot);
	}
	// 在AVL樹中插入值為data的節點
	bool Insert(const T& data)
	{
		//根節點為空
		if (_pRoot == nullptr)
		{
			_pRoot = new Node(data);
			return true;
		}
		else
		{
			//根節點不為空
			Node* cur = _pRoot;
			Node* parent = nullptr;
			//尋找插入位置
			while (cur)
			{
				if (data < cur->_data)
				{
					parent = cur;
					cur = cur->_pLeft;
				}
				else if (data > cur->_data)
				{
					parent = cur;
					cur = cur->_pRight;
				}
				else
				{
					cout << "數據冗餘，插入" << data << "失敗" << endl;
					return false;
				}
			}
			//找到了插入位置,插入
			cur = new Node(data);
			if (data < parent->_data)
			{
				parent->_pLeft = cur;
			}
			else
			{
				parent->_pRight = cur;
			}
			cur->_pParent = parent;
			//修正平衡因子
			while (parent)
			{
				if (cur == parent->_pLeft)
				{
					parent->_bf--;
				}
				else
				{
					parent->_bf++;
				}
				if (parent->_bf == 0)
				{
					//無需向上調整
					break;
				}
				else if (parent->_bf == 1 || parent->_bf == -1)
				{
					//繼續向上調整
					cur = parent;
					parent = parent->_pParent;
				}
				else if (parent->_bf == 2 || parent->_bf == -2)
				{
					if (parent->_bf == -2 && cur->_bf == -1)
					{
						//右單旋
						RotateR(parent);
					}
					else if (parent->_bf == 2 && cur->_bf == 1)
					{
						//左單旋
						RotateL(parent);
					}
					else if (parent->_bf == -2 && cur->_bf == 1)
					{
						//左右雙旋
						RotateLR(parent);
					}
					else if (parent->_bf == 2 && cur->_bf == -1)
					{
						//右左雙旋
						RotateRL(parent);
					}
					break;
				}
				else
				{
					cout << "AVL樹高度異常" << endl;
					assert(false);
				}
			}
		}
	}
	// AVL樹的驗證
	bool IsAVLTree()
	{
		return _IsAVLTree(_pRoot);
	}
private:
	// 根據AVL樹的概念驗證pRoot是否為有效的AVL樹
	bool _IsAVLTree(Node* pRoot)
	{
		if (pRoot == nullptr)
		{
			return true;
		}
		int HeightL = _Height(pRoot->_pLeft);
		int HeightR = _Height(pRoot->_pRight);
		int bf = HeightR - HeightL;
		if (abs(bf) >= 2)
		{
			cout << "高度差異常" << endl;
			return false;
		}
		else if (bf != pRoot->_bf)
		{
			cout << "平衡因子異常" << endl;
			return false;
		}
		return _IsAVLTree(pRoot->_pLeft) && _IsAVLTree(pRoot->_pRight);
	}
	size_t _Height(Node* pRoot)
	{
		if (pRoot == nullptr)
		{
			return 0;
		}
		size_t LeftHeight = _Height(pRoot->_pLeft);
		size_t RightHeight = _Height(pRoot->_pRight);
		return (LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1);
	}
	// 右單旋
	void RotateR(Node* pParent)
	{
		Node* NodeL = pParent->_pLeft;
		Node* NodeLR = NodeL->_pRight;
		Node* pParentParent = pParent->_pParent;
		//修正向下關係
		pParent->_pLeft = NodeLR;
		NodeL->_pRight = pParent;
		//修正向上關係
		pParent->_pParent = NodeL;
		if (NodeLR)
		{
			NodeLR->_pParent = pParent;
		}
		//修正外部關係
		if (pParentParent == nullptr)
		{
			_pRoot = NodeL;
			NodeL->_pParent = nullptr;
		}
		else
		{
			if (pParentParent->_pLeft == pParent)
			{
				pParentParent->_pLeft = NodeL;
			}
			else
			{
				pParentParent->_pRight = NodeL;
			}
			NodeL->_pParent = pParentParent;
		}
		//修正平衡因子
		pParent->_bf = 0;
		NodeL->_bf = 0;
	}
	// 左單旋
	void RotateL(Node* pParent)
	{
		Node* NodeR = pParent->_pRight;
		Node* NodeRL = NodeR->_pLeft;
		Node* pParentParent = pParent->_pParent;
		//修正向下關係
		pParent->_pRight = NodeRL;
		NodeR->_pLeft = pParent;
		//修正向上關係
		pParent->_pParent = NodeR;
		if (NodeRL)
		{
			NodeRL->_pParent = pParent;
		}
		//修正外部關係
		if (pParentParent == nullptr)
		{
			_pRoot = NodeR;
			NodeR->_pParent = nullptr;
		}
		else
		{
			if (pParentParent->_pLeft == pParent)
			{
				pParentParent->_pLeft = NodeR;
			}
			else
			{
				pParentParent->_pRight = NodeR;
			}
			NodeR->_pParent = pParentParent;
		}
		//修正平衡因子
		NodeR->_bf = 0;
		pParent->_bf = 0;
	}
	// 右左雙旋
	void RotateRL(Node* pParent)
	{
		Node* NodeR = pParent->_pRight;
		Node* NodeRL = NodeR->_pLeft;
		int bf = NodeRL->_bf;
		RotateR(NodeR);
		RotateL(pParent);
		//校正平衡因子
		if (bf == 0)
		{
			pParent->_bf = 0;
			NodeR->_bf = 0;
			NodeRL->_bf = 0;
		}
		else if (bf == 1)
		{
			pParent->_bf = -1;
			NodeR->_bf = 0;
			NodeRL->_bf = 0;
		}
		else if (bf == -1)
		{
			pParent->_bf = 0;
			NodeR->_bf = 1;
			NodeRL->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}
	// 左右雙旋
	void RotateLR(Node* pParent)
	{
		Node* NodeL = pParent->_pLeft;
		Node* NodeLR = NodeL->_pRight;
		int bf = NodeLR->_bf;
		RotateL(NodeL);
		RotateR(pParent);
		//校正平衡因子
		if (bf == 0)
		{
			pParent->_bf = 0;
			NodeL->_bf = 0;
			NodeLR->_bf = 0;
		}
		else if (bf == 1)
		{
			pParent->_bf = 0;
			NodeL->_bf = -1;
			NodeLR->_bf = 0;
		}
		else if (bf == -1)
		{
			pParent->_bf = 1;
			NodeL->_bf = 0;
			NodeLR->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}
	void _Display(Node* ptr)
	{
		if (ptr == nullptr)
		{
			return;
		}
		_Display(ptr->_pLeft);
		cout << ptr->_data << ":" << ptr->_bf << " ";
		_Display(ptr->_pRight);
	}
private:
	Node* _pRoot;
};
void Test()
{
	AVLTree tree1;
	//常規測試
	//int a[] = { 1, 2, 3};
	//int a[] = {3, 2, 1};
	int a[] = {16, 15, 14, 17, 18, 13, 19, 20};
	//帶雙旋的測試
	//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	for (auto num : a)
	{
		tree1.Insert(num);
	}
	tree1.Display();
}
int main()
{
	Test();
	return 0;
}

mb61c46a7ab1eee 博客

mb61c46a7ab1eee 博客

博客 / 詳情