大家好，我們又見面了。這一期，我來給大家介紹一個高階數據結構：Trie 樹。

字典樹在計算機領域還是非常常見的，相信這篇文章一定會對大家有所幫助。

創作不易！！！別忘了一鍵三連~~~

廢話不多説，我們直接開啓這一期的內容。

一：字典樹的概念

Trie 樹又叫字典樹或前綴樹，是一種能夠快速處理插入和查詢字符串的數據結構。它利用字符串的公共前綴，將字符串組織成一顆樹形結構，從而大大提高了存儲以及查詢的效率。

注：哈希表和紅黑樹也可以做到快速處理插入和查詢字符串的操作。但這並不能説明字典樹的設計是多餘的，字典樹可以做到一些它們做不到的事情。

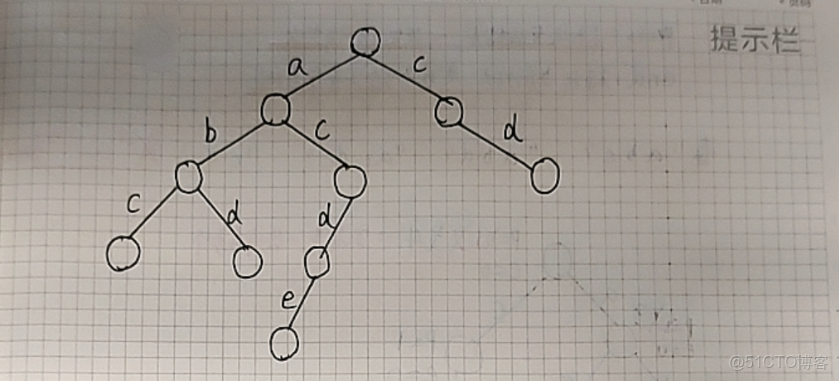
我們可以把字典樹想象成為一顆多叉樹，其中每一條邊代表一個字符，從根節點到某個節點的路徑就代表了一個字符串。例如，要存儲 "abc" "abd" "acde" 以及 "cd"

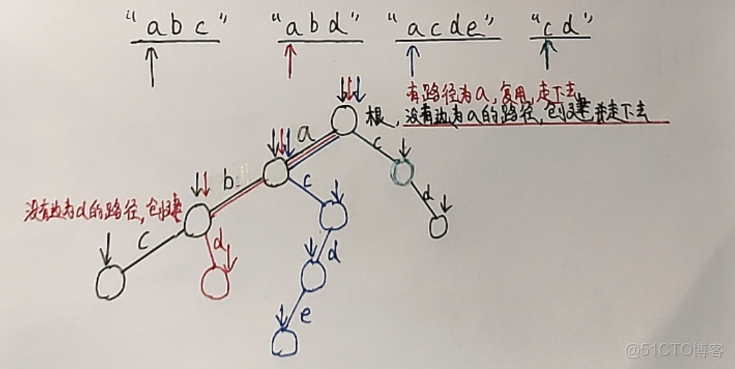
上述字典樹構建過程：（自己多模擬幾遍）

1. 一個字符串一個字符串遍歷，當遍歷到某一個字符串時，遍歷它的每一個字符。

2. 第一個字符對應樹的第一二層之間的邊，第二個字符對應樹的第二三層之間的邊，依次類推。

3. 初始狀態下，字典樹只有一個根節點（第一層）。

2. 從根節點開始，如果有對應這一個字符的路徑，就複用，走下去，如果沒有，就創建路徑。

這樣創建完畢之後，處理查詢字符串的邏輯也與插入字符串類似。一層一層往下走。

比如：查詢字符串 "acde" "ad" ，一層一層往下走，發現 "acde" 存在，"ad" 並不存在。

自己下去模擬，詳細過程這裏不贅述了。

但是按照上面方式創建出的字典樹是有一定問題的。比如：

1. 我們我們想要查詢字符串 "ac" 是否存在，按照上述方式是會判斷它存在的，但是實際並沒有插入 "ac" 字符串。

2. 再比如，如果我們之前插入了 "acde"，現在又要插入 "ac"，這時實際就存在 "ac" 字符串了。

3. 再比如，如果我們插入了很多個 "ac" 字符串，查詢的時候怎麼才能知道插入了多少個呢？？？

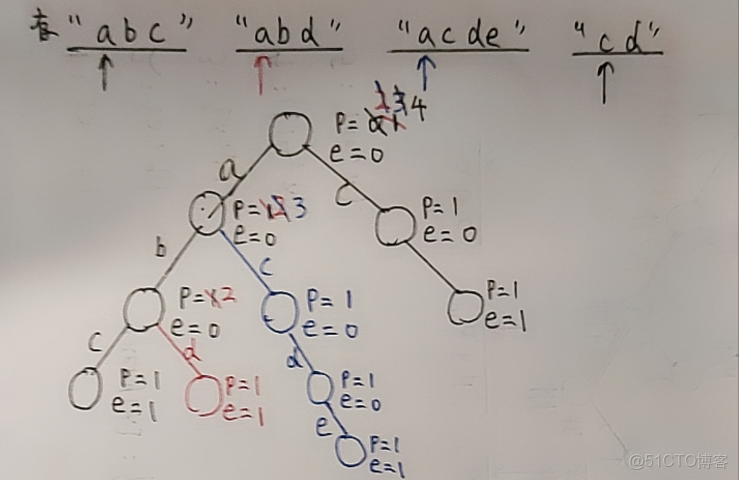
基於上述問題，我們在字典樹的每一個結點上多維護兩個變量：

1. pass：標記當前結點一共出現 / 經過了多少次。

2. end：標記當前結點是以多少個字符串為結尾。

然後我們在插入字符串的同時維護好每一個節點的信息，就可以解決上面的問題了。

這樣的話，就很好的解決了上面的問題。

二：字典樹的作用

當我們在字典樹的每一個節點位置，額外維護一些信息時，就可以做到很多事情：

1. 查詢某一個單詞是否出現過，並且出現過幾次。

2. 查詢有多少個單詞是以某一個字符串為前綴。

3. 查詢所有以某個前綴開頭的單詞。（dfs 子樹）

三：字典樹的模擬實現

我們實現一個能夠查詢某單詞出現次數以及查詢有多少個單詞是以某個字符串為前綴的字典樹。

默認全是小寫字母 a~z：

1. 準備工作

#include 
#include 
using namespace std;
const int N = 1e6 + 10;
int tree[N][26], p[N], e[N];
int idx;

N：表示所有的字符串中一共出現了多少個字符。（字典樹的節點個數最差情況都不復用）

tree[i]：表示 i 號結點的孩子信息

tree[i][0]：表示 'a' 的路徑信息

tree[i][1]：表示 'b' 的路徑信息

tree[i][2]：表示 'c' 的路徑信息

…………

p[i]：表示 i 號結點的 pass 信息

e[i]：表示 i 號結點的 end 信息

idx：新來一個字符之後，為它分配位置。

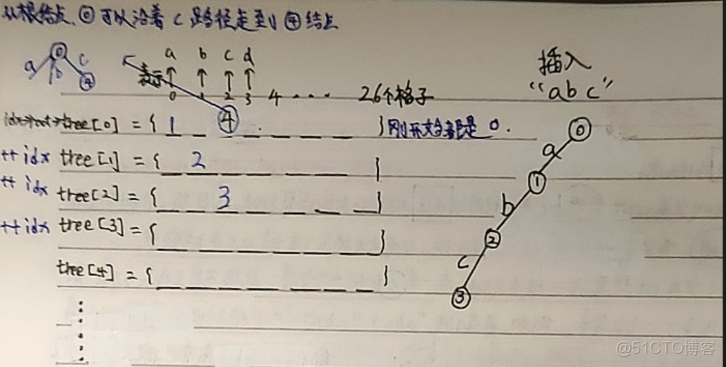
接下來通過一張圖深刻理解一下 tree 數組的作用：

2. 插入字符串

void insert(string& s)
{
	int cur = 0; // 從根節點開始考慮
	p[cur]++;    // 這個格子經過一次
	for (auto ch : s)
	{
		int path = ch - 'a'; // 對應路徑編號
		// 如果沒有路,自己開闢一條路
		if (tree[cur][path] == 0) tree[cur][path] = ++idx;
		cur = tree[cur][path]; // 走下去
		p[cur]++; // 維護節點的 pass 信息
	}
	e[cur]++; // 最後別忘了維護 e 信息
}

3. 查詢字符串出現的次數

int find(string& s)
{
	int cur = 0; // 從根節點開始
	for (auto ch : s)
	{
		int path = ch - '0'; // 路徑編號
		if (tree[cur][path] == 0) return 0; // 沒有路，找不到
		cur = tree[cur][path]; // 走下去
	}
	return e[cur]; // 找到了，返回出現的次數
}

4. 查詢有多少個單詞以字符串 s 為前綴

int find_pre(string& s)
{
	int cur = 0;
	for (auto ch : s)
	{
		int path = ch - '0';
		if (tree[cur][path] == 0) return 0;
		cur = tree[cur][path];
	}
	return p[cur];
}

建議：一定要下去之後自己多找幾個字符串模擬幾遍，只要明白了原理，代碼是很簡單的。

好的，這一期的分享就到這裏了，我們下一期再見。