目錄
寬度優先搜索的核心思想
算法實現步驟
BFS的特點和應用場景
BFS 在樹結構的應用
寬度優先搜索的核心思想
想象一下你在玩一個迷宮遊戲,你站在起點,想知道最快到達終點的路線。BFS的策略是:
首先探索所有起點直接相連的位置(第一層)。
然後探索所有與第一層位置直接相連的、且未被訪問過的位置(第二層)。
接着探索所有與第二層位置直接相連的、且未被訪問過的位置(第三層)。
... 以此類推,直到找到終點或者遍歷完所有能到達的點。
這種“由近及遠”的搜索方式,保證了一旦找到目標,所用的步數(或路徑長度)一定是最短的。
算法實現步驟
BFS通常使用一個隊列(Queue) 這種數據結構來輔助實現。隊列的特點是“先進先出”(FIFO),這正好符合我們“先訪問的節點,其鄰居也先被訪問”的需求。
步驟分解:
初始化:選擇一個起始節點,將其標記為“已訪問”。將該起始節點放入隊列。
循環執行以下步驟,直到隊列為空:
a. 出隊:從隊列的頭部取出一個節點(我們稱它為“當前節點”)。
b. 處理:訪問該節點(例如,檢查它是否是目標節點,或者進行其他操作)。
c. 探索鄰居:檢查當前節點的所有“未訪問”的鄰居節點。
* 將每一個未訪問的鄰居節點標記為“已訪問”。
* 將這些鄰居節點依次放入隊列的尾部。結束:當隊列為空時,説明所有從起點可達的節點都已經被訪問過了,算法結束。
一個生動的例子
0
/ \
1 2
/ \ \
3 4 5步驟模擬:
|
步驟
|
隊列狀態 (隊首<- ... <-隊尾)
|
當前節點
|
訪問順序
|
動作説明
|
|
初始
|
[0]
|
-
|
-
|
將起點0放入隊列
|
|
1
|
[1, 2]
|
0 |
0 |
取出0,訪問它。將0的未訪問鄰居1, 2加入隊列。
|
|
2
|
[2, 3, 4]
|
1 |
1 |
取出1,訪問它。將1的未訪問鄰居3, 4加入隊列。
|
|
3
|
[3, 4, 5]
|
2 |
2 |
取出2,訪問它。將2的未訪問鄰居5加入隊列。
|
|
4
|
[4, 5]
|
3 |
3 |
取出3,訪問它。3沒有未訪問的鄰居。
|
|
5
|
[5]
|
4 |
4 |
取出4,訪問它。4沒有未訪問的鄰居。
|
|
6
|
[]
|
5 |
5 |
取出5,訪問它。5沒有未訪問的
|
最終的訪問順序(BFS遍歷序列)是:0, 1, 2, 3, 4, 5。你可以看到,這正是一層一層輸出的結果。
BFS的特點和應用場景
特點:
完備性:如果解存在,BFS一定能找到。
最優性:在無權圖中,BFS找到的路徑一定是最短路徑。
空間複雜度高:在最壞情況下,需要存儲一整層的節點,對於分支因子為b的樹,第d層有b^d個節點,空間複雜度為O(b^d)。
應用場景:
圖的連通性:判斷兩個節點是否連通。
最短路徑:在無權圖中求兩點間的最短路徑。
迷宮求解:找到從起點到終點的最短路徑。
社交網絡:查找“度”關係(例如,尋找三度好友)。
序列變換(如單詞接龍問題)。
樹的層序遍歷。
BFS 在樹結構的應用
層序遍歷
題目鏈接
解析:採用深度優先搜索,但難點是不知道每層具體有多少結點,也就不知道要把多少結果放在數組的同一行,解決方法是在遍歷隊列之前用一個變量先記錄一下隊列的長度,然後執行長度次訪問隊頭的操作,執行完後,再次記錄隊列的長度,下一次遍歷隊列時就訪問長度次......以此類推。
class Solution {
public:
vector> levelOrder(Node* root) {
queue q;
vector> ret;
if(root) q.push(root);
int i = 0;
while(!q.empty())
{
ret.resize(i + 1); // 為下一次記錄結果開闢空間
int sz = q.size(); // 記錄這一層的結點個數
while(sz--)
{
// 訪問對頭
ret[i].push_back((q.front())->val);
// 把對頭的子結點加入隊列
for(auto j : (q.front())->children)
{
q.push(j);
}
// 對頭已經訪問完了,出隊列
q.pop();
}
i++;
}
return ret;
}
};*>題目鏈接
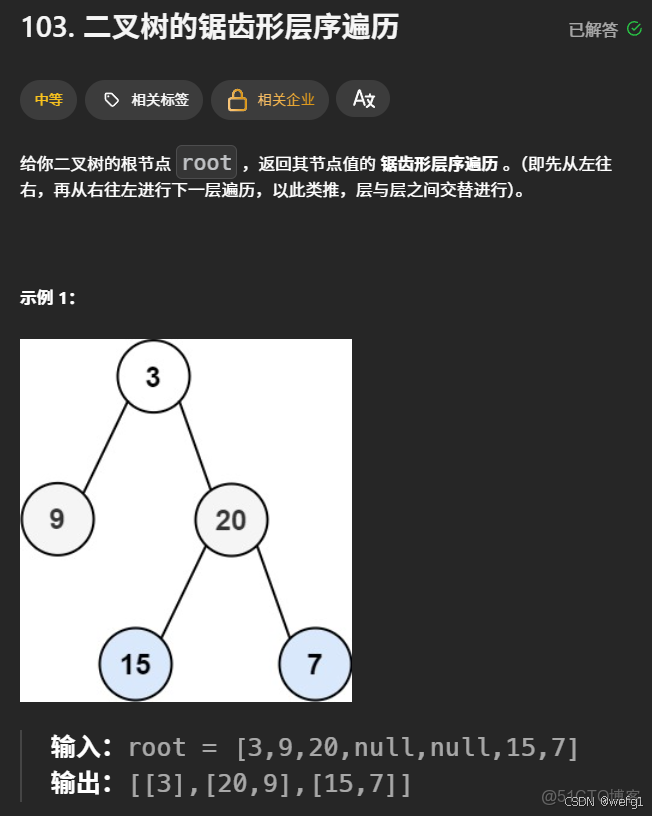
解析:先進行二叉樹的層序遍歷,最後將結果數組的對應部分進行逆序
class Solution {
public:
vector> zigzagLevelOrder(TreeNode* root) {
vector> ret;
queue q;
int sz = 0;
int i = 0;
if(root) q.push(root);
while(!q.empty())
{
sz = q.size();
ret.resize(i + 1);
while(sz--)
{
TreeNode* top = q.front();
ret[i].push_back(top->val);
q.pop();
if(top->left) q.push(top->left);
if(top->right) q.push(top->right);
}
i++;
}
for(int j = 1; j < ret.size(); j += 2)
{
reverse(ret[j].begin(),ret[j].end());
}
return ret;
}
};*>題目鏈接
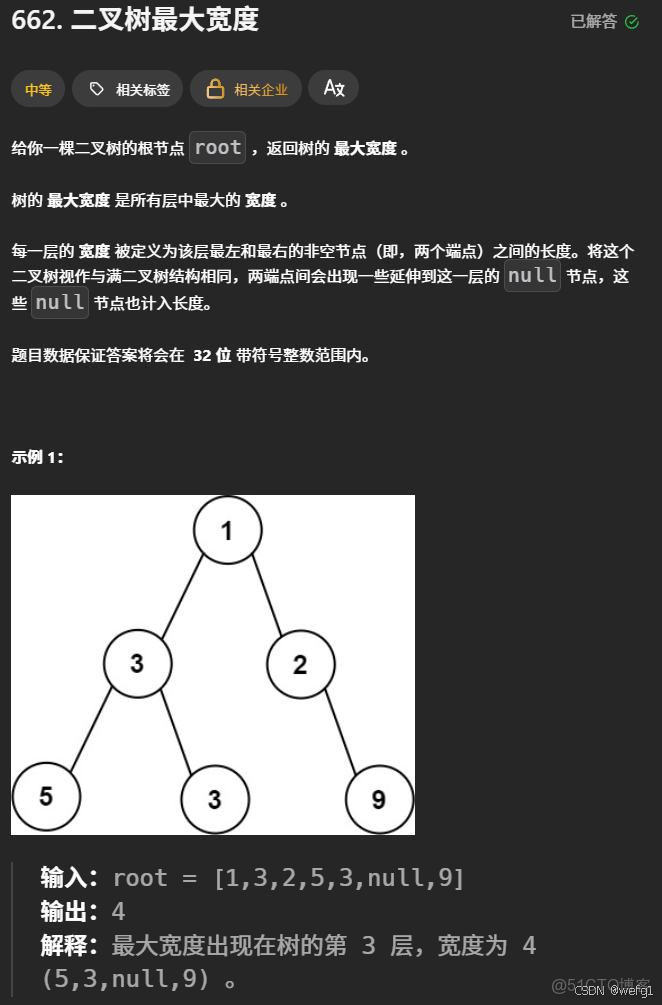
解析:以從左到右,從上到下,從根結點開始為 1,依次對非空結點進行編號,可以發現如果根結點的編號為 n ,那麼它的左孩子和右孩子的編號分別為 2*n 和 2*n + 1,樹某行的寬度 = 最右邊的結點編號 - 最左邊結點編號 + 1。對樹進行層序遍歷,隊列中每個元素存儲結點和結點的編號。
lass Solution {
public:
int widthOfBinaryTree(TreeNode* root) {
queue> q;
if(root) q.push(make_pair(root,1));
unsigned maxlen = 0;
while(!q.empty())
{
pair front = q.front();
pair back = q.back();
if(back.second - front.second + 1 > maxlen)
maxlen = back.second - front.second + 1;
int sz = q.size();
while(sz--)
{
pair front = q.front();
if((front.first)->left)
q.push(make_pair((front.first)->left,front.second * 2));
if((front.first)->right)
q.push(make_pair((front.first)->right,front.second * 2 + 1));
q.pop();
}
}
return maxlen;
}
};*,unsigned>*,unsigned>*,unsigned>