兜兜轉轉了半天,發現還是Carl寫的好。
看過動態規劃-基礎的讀者,大概都清楚。
動態規劃是將大問題,分解成子問題。並將子問題的解儲存下來,避免重複計算。
而揹包問題,就是動態規劃延申出來的一個大類。
而01揹包,就隸屬於揹包問題。
那什麼又是01揹包呢?
01揹包
有n件物品,與一次最多能背w重量的揹包。第i件物品,重量為weight[i],得到的價值為value[i]。
每件物品只能用一次,求解,將那些物品裝入揹包內,物品的價值總和最大。
|
重量(weight)
|
價值(value)
|
|
|
物品0
|
1
|
15
|
|
物品1
|
3
|
20
|
|
物品2
|
4
|
30
|
這是一個標準的揹包問題,很多一看到這個,就直接想起用動態規劃,而忽略了暴力解法。
這是因為沒有 自下而上 思考的結果。
如下代碼,一般動態規劃問題,都是能通過回溯解決,因為每個物品都有兩種可能(狀態),
被放入揹包,或者不放入揹包。
// 全局變量用於記錄最大價值
int maxValue = 0;
// 物品的重量和價值數組
vector weights = {1, 3, 4, 5, 6};
vector values = {1, 3, 4, 5, 6};
// 揹包容量
int capacity = 10;
// 回溯函數
void backtrack(int index, int currentWeight, int currentValue) {
// 如果已經遍歷完所有物品
if (index == weights.size()) {
// 更新最大價值
if (currentValue > maxValue) {
maxValue = currentValue;
}
return;
}
// 不選擇當前物品 - 01揹包中的0
backtrack(index + 1, currentWeight, currentValue);
// 選擇當前物品 - 01揹包中的1
if (currentWeight + weights[index] <= capacity) {
backtrack(index + 1, currentWeight + weights[index], currentValue + values[index]);
}
}如上的回溯算法,每個問題都有兩個解法,通過暴力解決,但通常這種解法,是O(2^n)的時間複雜度,隨着數量的增加。
呈指數級上升。
而動態規劃僅僅需要O(N*M)就可以解決。
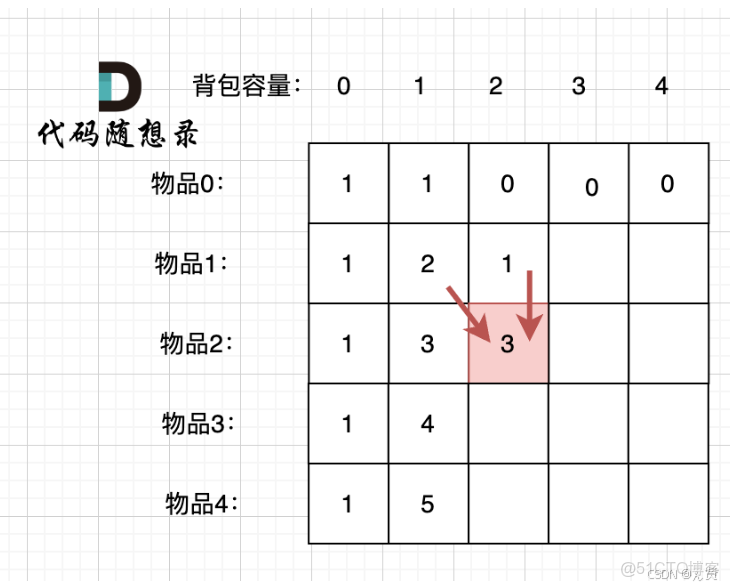
第一步:下標含義
dp[i][j]表示將前i件物品裝進限重為j的揹包可以獲得的最大價值, 0<=i<=N, 0<=j<=W第二步:推導公式
那麼我們可以將dp[0][0...W]初始化為0,表示將前0個物品(即沒有物品),裝入書包的最大價值為0。那麼當i>0時,dp[i][j]有兩種情況:
- 不裝入第i件物品,即
dp[i−1][j]; - 裝入第i件物品(前提是能裝下),即dp[i-1][j-weight[i]]+value[i]。
第三步:書寫代碼
dp[weight.size()][bagweight + 1];
// weight數組的大小 就是物品個數
for(int i = 1; i < weight.size(); i++) { // 遍歷物品
for(int j = 0; j <= bagweight; j++) { // 遍歷揹包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}壓縮
遞推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
看到 dp[i][j] 與 dp[i-1][...] 的
大家都可以發現,dp都由上一行推導出來的(也就是把dp[i - 1]那一層拷貝到dp[i]上),所以可以壓縮代碼。
把二維數組,壓縮為一維滾動數組。
這也就是滾動數組的由來,需要滿足的條件是上一層可以重複利用,直接拷貝到當前層。
需要注意的是,為了防止上一層循環的dp[0,...,j-1]被覆蓋,循環的時候 j 只能逆向枚舉
如下:
for(int i = 0; i < weight.size(); ++i){
for(int j = bagWeight; j>=weight[i]; j--){
dp[j] = max( dp[j], dp[j-weight[i]]+value[i] );
}
}大綱
1、分割等和子集
最後一塊石頭的重量 II
目標和
一和零
題目
1、分割等和子集
給你一個 只包含正整數 的 非空 數組
nums。請你判斷是否可以將這個數組分割成兩個子集,使得兩個子集的元素和相等。
示例 1:
輸入:nums = [1,5,11,5] 輸出:true 解釋:數組可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
輸入:nums = [1,2,3,5] 輸出:false 解釋:數組不能分割成兩個元素和相等的子集。
提示:
1 <= nums.length <= 2001 <= nums[i] <= 100
class Solution {
// 最大也就意味着最接近
// 能通過動態規劃解決的,都能通過回溯解決
// 每個數字都有兩種狀態,被選中,或者不被選中
// 只有單純的數字,那麼數字的大小是重量,也是價值。
public:
bool canPartition(vector& nums) {
int cur = 0;
for(int i:nums) cur+=i;
int sum = cur/2;
if(sum*2 != cur) return false; // 意外情況,直接排除
vector dp(sum+1,0);
for(int i=0; i=nums[i]; --j){
dp[j] = max(dp[j], dp[j-nums[i]]+nums[i]);
}
}
return sum==dp[sum]?true:false;
}
};();>2、最後一塊石頭的重量 II
有一堆石頭,用整數數組
stones表示。其中stones[i]表示第i塊石頭的重量。每一回合,從中選出任意兩塊石頭,然後將它們一起粉碎。假設石頭的重量分別為
x和y,且x <= y。那麼粉碎的可能結果如下:
- 如果
x == y,那麼兩塊石頭都會被完全粉碎;- 如果
x != y,那麼重量為x的石頭將會完全粉碎,而重量為y的石頭新重量為y-x。最後,最多隻會剩下一塊 石頭。返回此石頭 最小的可能重量 。如果沒有石頭剩下,就返回
0。
示例 1:
輸入:stones = [2,7,4,1,8,1] 輸出:1 解釋: 組合 2 和 4,得到 2,所以數組轉化為 [2,7,1,8,1], 組合 7 和 8,得到 1,所以數組轉化為 [2,1,1,1], 組合 2 和 1,得到 1,所以數組轉化為 [1,1,1], 組合 1 和 1,得到 0,所以數組轉化為 [1],這就是最優值。
示例 2:
輸入:stones = [31,26,33,21,40] 輸出:5
提示:
1 <= stones.length <= 301 <= stones[i] <= 100
為啥要分兩堆->一直在動態的動態的維護,從第一塊進入開始,一直在動態的維護兩堆的平衡。
class Solution {
// 對吶,只要讓兩撥石頭血拼就行!
// 但是,為啥要讓兩撥石頭血拼?
// 圖片上附上解析,希望以後能看懂
public:
int lastStoneWeightII(vector& stones) {
int sum = 0;
for(int i : stones) sum+=i;
int cur = sum;
sum>>=1; // 右移2位,相當於除以2;
vector dp(sum+1, 0);
for(int i=0; i=stones[i]; --j){
dp[j] = max(dp[j],dp[j-stones[i]]+stones[i]);
}
}
return cur-2*dp[sum];
}
};();>3、目標和
給你一個非負整數數組
nums和一個整數target。向數組中的每個整數前添加
'+'或'-',然後串聯起所有整數,可以構造一個 表達式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然後串聯起來得到表達式"+2-1"。返回可以通過上述方法構造的、運算結果等於
target的不同 表達式 的數目。
示例 1:
輸入:nums = [1,1,1,1,1], target = 3 輸出:5 解釋:一共有 5 種方法讓最終目標和為 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3
示例 2:
輸入:nums = [1], target = 1 輸出:1
提示:
1 <= nums.length <= 200 <= nums[i] <= 10000 <= sum(nums[i]) <= 1000-1000 <= target <= 1000
class Solution {
// 如果用暴力解法,本題也是能做的
// 但是如果我不暴力呢?
// 瞭解過答案之後,就發現這道題目,純純是一道推理題。
// 用方法就行推理,真tm是一道推理題
// (cur+)+(cur-) = target;
// (cur+)-(cur-) = target;
// cur = (sum-target)/2; 由此公式推導
// 只要找到cur就OK了
// 當sum為0時,代表總和與target相同,都只有一種情況
public:
int findTargetSumWays(vector& nums, int target) {
int cur = 0;
for(int i:nums) cur+=i;
int sum = (cur-target)>>1;
if(sum*2!=cur-target||sum<0) return 0; // 直接就沒有可能了
vector dp(sum+1);
dp[0]=1;
// 公式推導出來的正整數
for(int i=0; i=nums[i]; --j){
dp[j]=dp[j-nums[i]]+dp[j];
}
}
return dp[sum];
}
};
// ???我的腦袋裏,有個大大的問題?這能過??();>4、一和零
給你一個二進制字符串數組
strs和兩個整數m和n。請你找出並返回
strs的最大子集的長度,該子集中 最多 有m個0和n個1。如果
x的所有元素也是y的元素,集合x是集合y的 子集 。
示例 1:
輸入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3 輸出:4 解釋:最多有 5 個 0 和 3 個 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。 其他滿足題意但較小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不滿足題意,因為它含 4 個 1 ,大於 n 的值 3 。
示例 2:
輸入:strs = ["10", "0", "1"], m = 1, n = 1 輸出:2 解釋:最大的子集是 {"0", "1"} ,所以答案是 2 。
提示:
1 <= strs.length <= 6001 <= strs[i].length <= 100strs[i]僅由'0'和'1'組成1 <= m, n <= 100
class Solution {
// 直接就幹到n的三次方了!我的天吶,太牛了
public:
int findMaxForm(vector& strs, int m, int n) {
vector> dp(m+1,vector(n+1,0));
for(string str : strs){
int num0=0,num1=0;
for(char c : str){
if(c=='0') num0++;
else num1++;
}
for(int i=m; i>=num0; --i){
for(int j=n; j>=num1; --j){
dp[i][j] = max(dp[i][j],dp[i-num0][j-num1]+1);
}
}
}
return dp[m][n];
}
};完結( ̄︶ ̄)↗ ,自己是收益匪淺啦
博客借鑑:
1、動態規劃之揹包問題系列
2、動態規劃:01揹包理論基礎