輸入：n = 4, k = 2
輸出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

輸入：n = 1, k = 1
輸出：[[1]]

class Solution {

    List<List<Integer>> result= new ArrayList<>();
    List<Integer> path = new LinkedList<>();

    public List<List<Integer>> combine(int n, int k) {
       
        backtrading(n, k, 1);
        return result;
    }


    public void backtrading(int n, int k, int startIndex){
        if(path.size() == k){
            result.add(new ArrayList<>(path));
            return;
        }

        for(int i = startIndex; i <= n; i++){
            path.add(i);
            backtrading(n, k, i+1);
            path.removeLast();
        }
    }
}

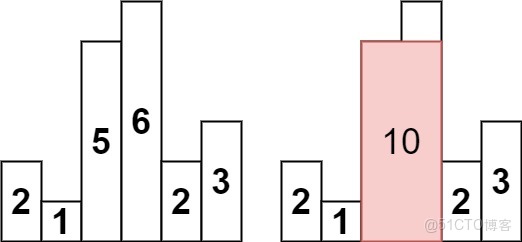
輸入：heights = [2,1,5,6,2,3]
輸出：10
解釋：最大的矩形為圖中紅色區域，面積為 10

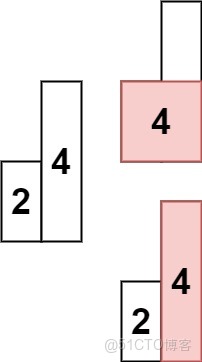
輸入： heights = [2,4]
輸出： 4

class Solution {
    public int largestRectangleArea(int[] heights) {
        //要找比主元素更小的，所以要用單調遞增棧，那麼找到第一個最小的就能解決棧內所有元素問題
        Deque<Integer> st = new ArrayDeque<>();
        int[] res = new int[heights.length + 2];
        //給初始列表收尾添加0邊界(相當於兩個虛擬柱子，這樣可以在求面積時讓每個柱子都計算到)
        for(int i = 0;i < heights.length;i++)
            res[i+1] = heights[i];
        int maxArea = 0; 
        for(int i = 0;i < res.length;i++){
            //入棧：遍歷元素大於棧頂元素
            //出棧：當遍歷元素小於棧頂元素，棧內元素出棧
            while(!st.isEmpty() && res[i] < res[st.peek()]){ //遇到了比棧頂更小的下標i，那麼右邊界就是i
                int topIntex = st.pop(); //當前要計算面積的柱子下標（出棧的就是要處理到了）
                int h = res[topIntex]; //要處理柱子的高
                //
                int leftIndex = st.peek(); //因為單調棧是遞增的，pop之後再次peek獲取的是上一個比棧頂元素小的元素，即左邊界
                int w = i - leftIndex - 1;
                maxArea = Math.max(maxArea,h * w);
            }
            st.push(i); //遇到比棧頂元素大的就一直入棧,注意棧內存放的是元素下標
        }
        return maxArea;
    }
}