85. 最大矩形
給定一個僅包含 0 和 1 、大小為 rows x cols 的二維二進制矩陣,找出只包含 1 的最大矩形,並返回其面積。
示例 1:
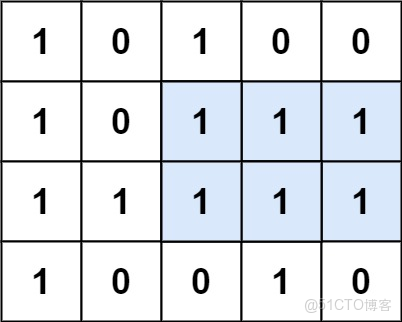
輸入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
輸出:6
解釋:最大矩形如上圖所示。示例 2:
輸入:matrix = [["0"]]
輸出:0示例 3:
輸入:matrix = [["1"]]
輸出:1
提示:
rows == matrix.lengthcols == matrix[0].length1 <= rows, cols <= 200matrix[i][j]為'0'或'1'
class Solution {
public int maximalRectangle(char[][] matrix) {
int n = matrix[0].length;
int[] h = new int[n]; // 高度數組:存儲每列當前行及上方連續'1'的個數
int res = 0;
for (char[] row : matrix) { // 遍歷每一行,更新高度數組並計算面積
for (int j = 0; j < n; j++) { // 逐列更新高度:'0'重置為0,'1'累加
h[j] = row[j] == '0' ? 0 : h[j] + 1;
}
res = Math.max(res, getMaxRect(h)); // 計算當前行為底的最大面積,更新全局最大值
}
return res;
}
private int getMaxRect(int[] h) {
int n = h.length;
int[] stk = new int[n + 2];
stk[0] = -1; // 棧底哨兵:索引-1(對應高度0),處理棧空邊界
int top = 0; // 棧頂指針:指向當前棧頂元素(初始為哨兵)
int maxA = 0;
for (int i = 0; i <= n; i++) { // 遍歷高度數組,末尾虛擬加-1(強制彈出剩餘元素)
int cur = i != n ? h[i] : -1;
// 棧頂高度>=當前高度時彈出,計算以棧頂高度為高的最大面積
while (top > 0 && h[stk[top]] >= cur) {
int height = h[stk[top--]]; // 彈出棧頂索引,獲取對應高度
int width = i - stk[top] - 1; // 寬度=右側小高度位置(i)-左側小高度位置(新棧頂)-1
maxA = Math.max(maxA, height * width);
}
stk[++top] = i; // 當前索引入棧,維持棧遞增特性
}
return maxA;
}
}