深層神經網絡
淺層神經網絡和深層神經網絡的主要區別在於隱藏層的多少。隱藏層的層數越多,神經網絡越深。
深層神經網絡的一些符號定義:
L L : 神經網絡的層數
n[l]n[l]: 第l l 層的神經單元個數
a[l]=g[l](z[l])a[l]=g[l](z[l]): 第l l 層的激活函數
W[l]W[l]: 第l l 層z[l]z[l]的權重
x=a[0] x = a [ 0 ] ,y^=a[L] y ^ = a [ L ]
深層神經網絡的前向傳播
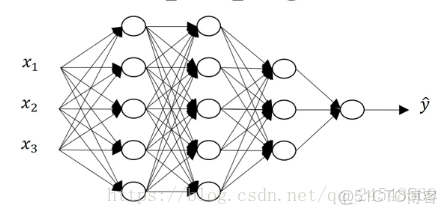
下圖是有3層隱藏層的神經網絡
一個樣本x在這個神經網絡中進行前向傳播的過程是
從中可以總結到規律:
多個樣本X在這個神經網絡中進行前向傳播的過程:
從中可以總結到規律:
因此在實現時可以使用for循環來實現。檢查代碼是否正確,可以檢查上述的公式得到的矩陣的維度是否正確。比如,
W[l] W [ l ] 的維度是 (n[l],n[l−1]) ( n [ l ] , n [ l − 1 ] ) , b[l] b [ l ] 的維度是 (n[l],1) ( n [ l ] , 1 ) , Z[l] Z [ l ] 的維度是 (n[l],m) ( n [ l ] , m ) 。確保這些參數的維度沒有問題,公式運算一般沒問題。
為什麼使用深層表示
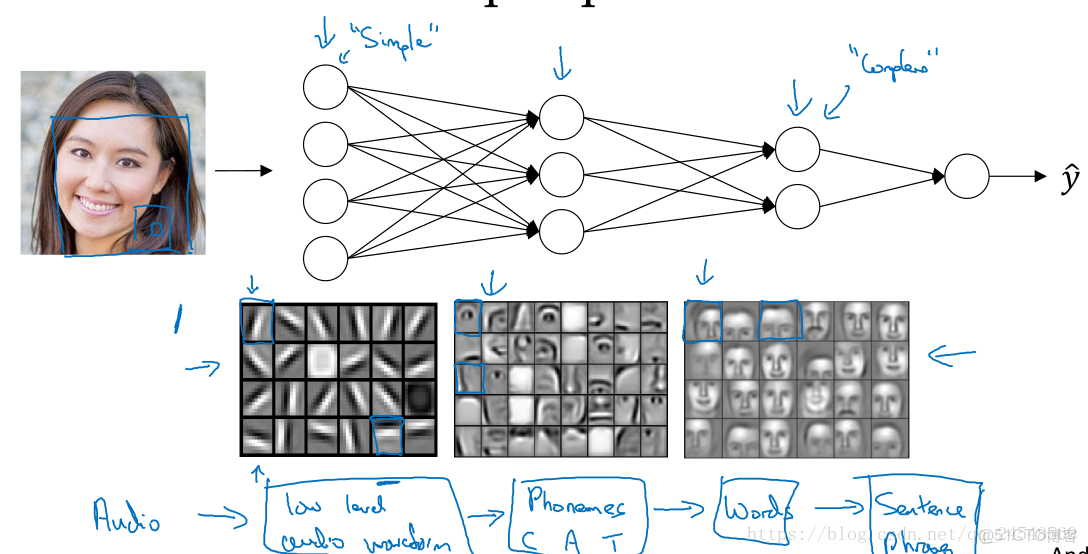
神經網絡越深,表現效果越好,為什麼呢?下面舉一些直觀的例子:
人臉識別的深層網絡的層數大概可以分成4組,第1組的層主要負責識別圖像的邊緣部分,可以稱為邊緣識別器。第2組的層根據第1組的層識別的邊緣部分識別人臉的某些部位,如眼睛,鼻子等,可以稱為人臉部位識別器。第3組的層根據第2組能夠識別出人臉。神經網絡中的隱藏層的層數越深,隱藏層的功能就越複雜。
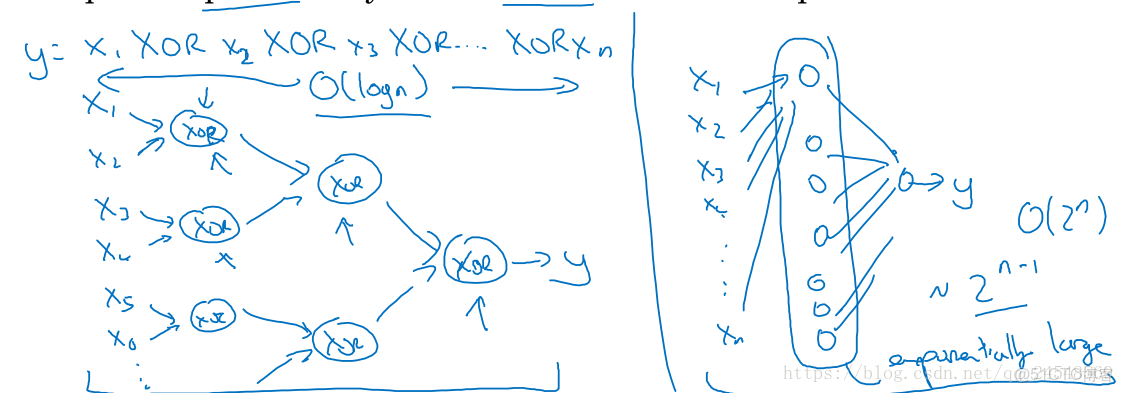
對於語音識別也是一樣的,淺層的隱藏層識別某種聲音,深一點的隱藏層識別單詞,更深一點的隱藏層識別語音的意思。另外一種解釋是,某些函數的功能只需要簡單的L層神經網絡就可以實現,如果使用層數更少的神經網絡,隱藏層就需要更多的隱藏單元。比如求n個數字的異或結果,深層的神經網絡需要O(logn)
O ( l o g n ) 個神經元,如果使用2層神經網絡,可能需要O(2n) O ( 2 n ) 個神經元,如下圖所示:
搭建深層神經網絡塊
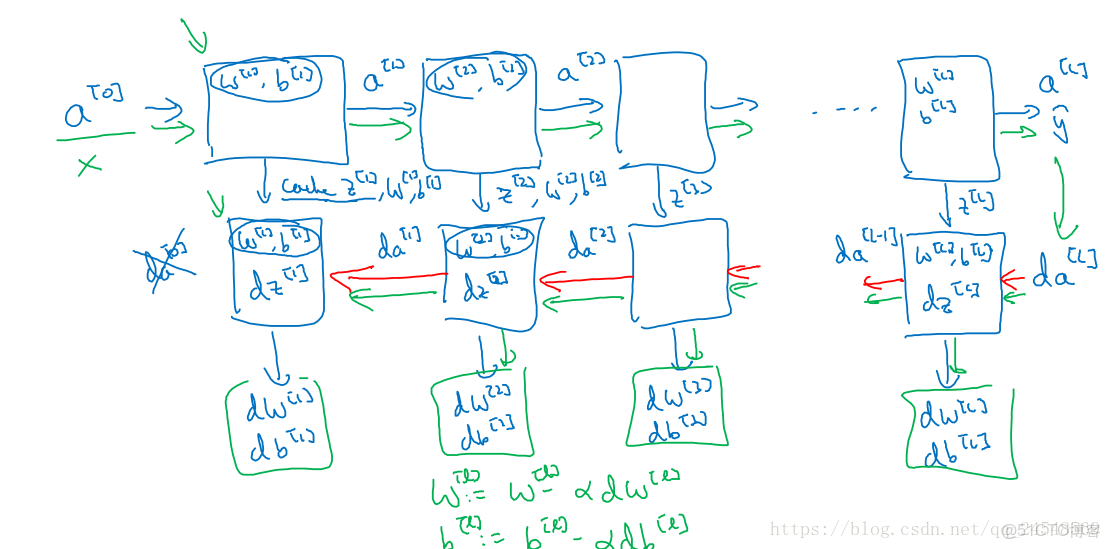
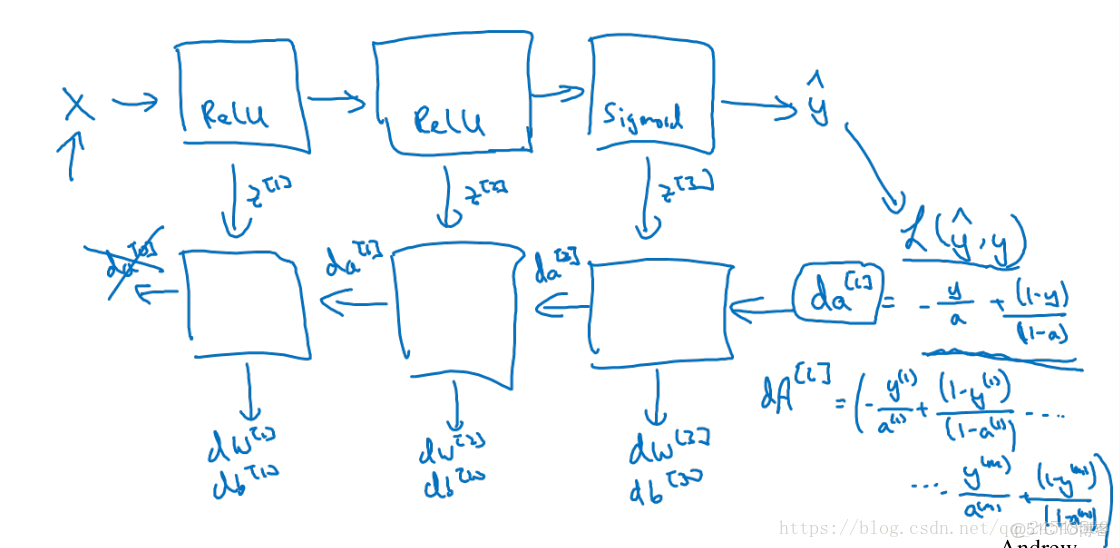
整個深層神經網絡的學習過程就是不斷地進行前向傳播、反向傳播和梯度下降,如下圖所示
把前向傳播和反向傳播兩個過程使用前向函數和反向函數表示,第l l 層的前向函數的輸入是a[l−1]a[l−1],輸出是a[l] a [ l ] ,第l l 層的反向函數的輸入是da[l]da[l]和z[l] z [ l ] ,輸出是da[l−1] d a [ l − 1 ] 、dW[l] d W [ l ] 和db[l] d b [ l ] 。在前向函數計算過程中,記得把z[l] z [ l ] 保存起來,然後傳遞給反向函數。
前向和反向傳播
這裏詳細介紹在每一層中前向和反向傳播的具體運算過程。
前向函數
Z[l] Z [ l ] 要緩存起來。
反向函數
輸入:da[l] d a [ l ]
輸出:da[l−1] d a [ l − 1 ] ,dW[l] d W [ l ] ,db[l] d b [ l ]
矢量化實現:
總結
不同的層,可能使用不同的激活函數,例如隱藏層使用ReLU函數,輸出層使用sigmoid函數。反向傳播開始的梯度是通過成本函數的導數來求的。成本函數的導數是
da[L]=−ya+1−y1−a d a [ L ] = − y a + 1 − y 1 − a
參數和超參數
參數:W[1] W [ 1 ] ,b[1] b [ 1 ] ,W[2] W [ 2 ] ,b[2] b [ 2 ] ⋯ ⋯
超參數:
- 學習率α α
- 梯度下降的迭代次數
- 隱藏層的層數
- 每層的隱藏單元
- 激活函數的選擇
- 還有其他一些,比如minibatch
超參數之所以稱為超參數,是因為超參數的值確定了之後,參數的值才確定。超參數的值需要自己決定,比如學習率α α 的最優值可能是0.01,也可能是0.05,尋找最優的超參數是一個參數調優的過程。超參數的最優值不是一成不變的,根據數據的不同,最優值也會不同。