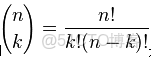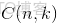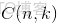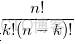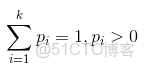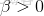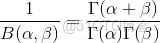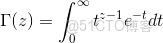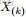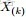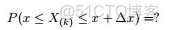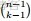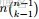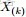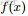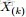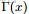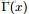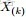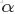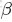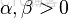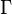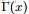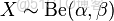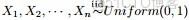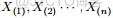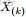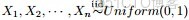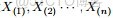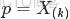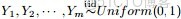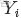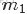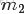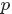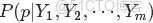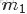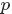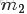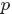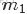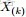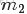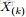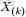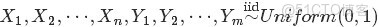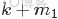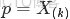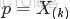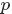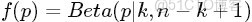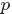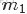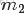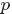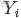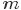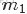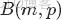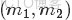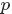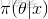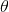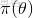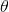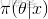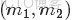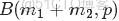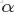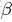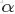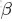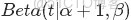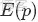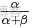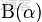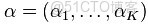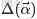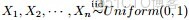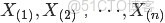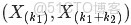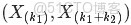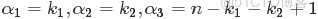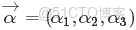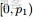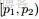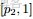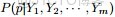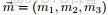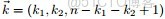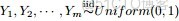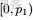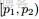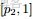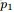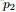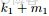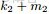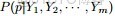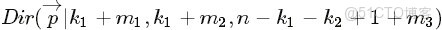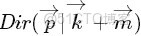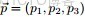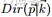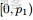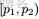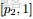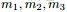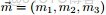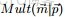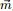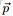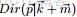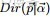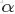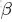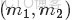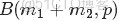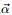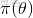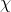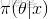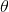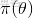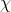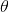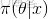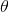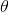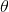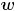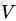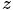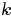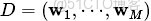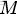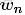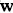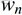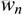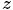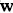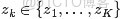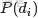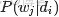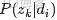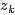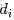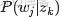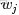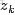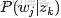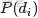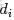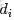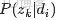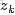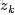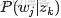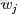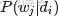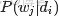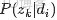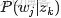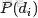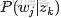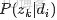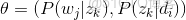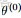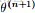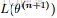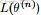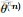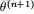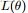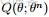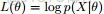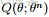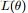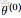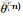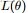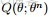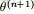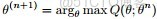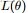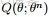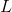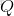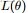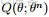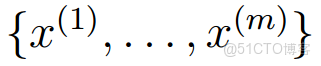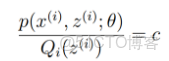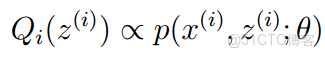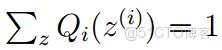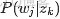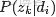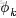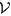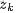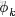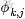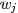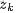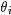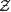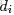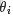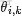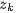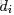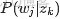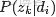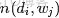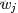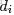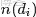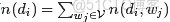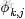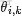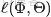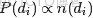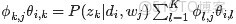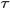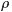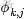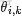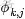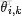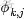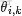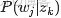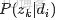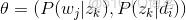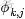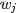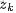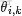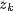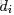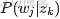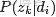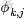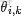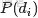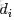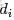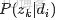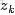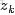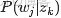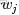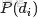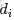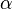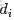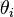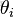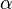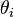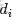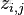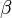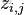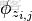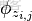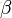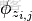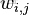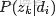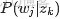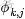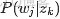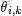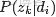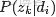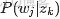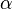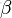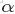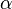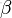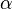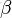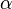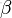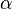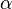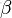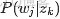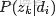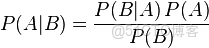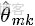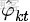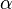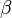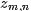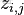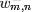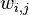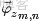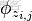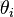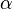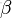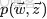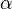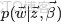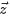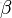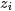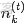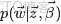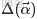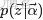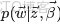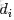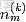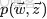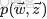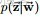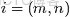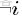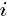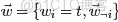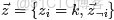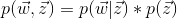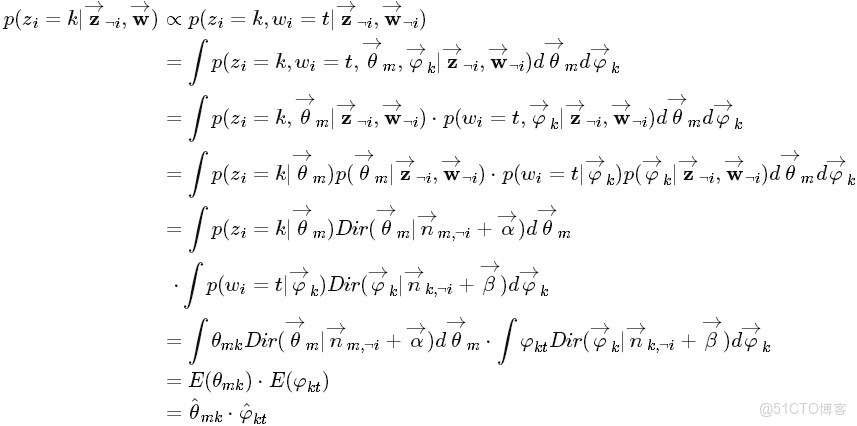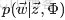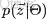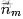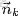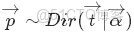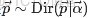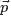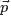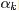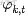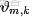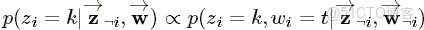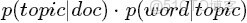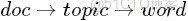1. 前言
2. gamma函數

1. 0 整體把握LDA
2. 1 gamma函數

3. beta分佈

1. 1 beta分佈
2. 2 Beta-Binomial 共軛
3. 3 共軛先驗分佈
4. 4 從beta分佈推廣到Dirichlet 分佈

1. Dirichlet 分佈

5. 1 Dirichlet 分佈
6. 2 Dirichlet-Multinomial 共軛

1. 主題模型LDA

7. 1 各個基礎模型
1. 11 Unigram model
2. 12 Mixture of unigrams model
8. 2 PLSA模型
1. 21 pLSA模型下生成文檔
2. 21 根據文檔反推其主題分佈
3. 211 EM算法的簡單介紹
4. 212 EM算法估計pLSA的兩未知參數
9. 3 LDA模型
1. 31 pLSA跟LDA的對比生成文檔與參數估計
2. 32 LDA生成文檔過程的進一步理解
3. 33 pLSA跟LDA的概率圖對比
4. 34 pLSA跟LDA參數估計方法的對比
5. 35 LDA參數估計Gibbs採樣

 

0 前言

    印象中，最開始聽説“LDA”這個名詞，是緣於rickjin在2013年3月寫的一個LDA科普系列，叫LDA數學八卦，我當時一直想看來着，記得還打印過一次，但不知是因為這篇文檔的前序鋪墊太長（現在才意識到這些“鋪墊”都是深刻理解LDA 的基礎，但如果沒有人幫助初學者提綱挈領、把握主次、理清思路，則很容易陷入LDA的細枝末節之中），還是因為其中的數學推導細節太多，導致一直沒有完整看完過。

    2013年12月，在我組織的Machine Learning讀書會第8期上，@夏粉_百度 講機器學習中排序學習的理論和算法研究，@沈醉2011 則講主題模型的理解。又一次碰到了主題模型，當時貌似只記得沈博講了一個汪峯寫歌詞的例子，依然沒有理解LDA到底是怎樣一個東西（但理解了LDA之後，再看沈博主題模型的PPT會很贊）。

    直到昨日下午，機器學習班 第12次課上，鄒講完LDA之後，才真正明白LDA原來是那麼一個東東！上完課後，趁熱打鐵，再次看LDA數學八卦，發現以前看不下去的文檔再看時竟然一路都比較順暢，一口氣看完大部。看完大部後，思路清晰了，知道理解LDA，可以分為下述5個步驟：

1. 一個函數：gamma函數
2. 四個分佈：二項分佈、多項分佈、beta分佈、Dirichlet分佈
3. 一個概念和一個理念：共軛先驗和貝葉斯框架
4. 兩個模型：pLSA、LDA（在本文第4 部分闡述）
5. 一個採樣：Gibbs採樣

    本文便按照上述5個步驟來闡述，希望讀者看完本文後，能對LDA有個儘量清晰完整的瞭解。同時，本文基於鄒講LDA的PPT、rickjin的LDA數學八卦及其它參考資料寫就，可以定義為一篇學習筆記或課程筆記，當然，後續不斷加入了很多自己的理解。若有任何問題，歡迎隨時於本文評論下指出，thanks。

 

0 前言

    印象中，最開始聽説“LDA”這個名詞，是緣於rickjin在2013年3月寫的一個LDA科普系列，叫LDA數學八卦，我當時一直想看來着，記得還打印過一次，但不知是因為這篇文檔的前序鋪墊太長（現在才意識到這些“鋪墊”都是深刻理解LDA 的基礎，但如果沒有人幫助初學者提綱挈領、把握主次、理清思路，則很容易陷入LDA的細枝末節之中），還是因為其中的數學推導細節太多，導致一直沒有完整看完過。

    2013年12月，在我組織的Machine Learning讀書會第8期上，@夏粉_百度 講機器學習中排序學習的理論和算法研究，@沈醉2011 則講主題模型的理解。又一次碰到了主題模型，當時貌似只記得沈博講了一個汪峯寫歌詞的例子，依然沒有理解LDA到底是怎樣一個東西（但理解了LDA之後，再看沈博主題模型的PPT會很贊）。

    直到昨日下午，機器學習班 第12次課上，鄒講完LDA之後，才真正明白LDA原來是那麼一個東東！上完課後，趁熱打鐵，再次看LDA數學八卦，發現以前看不下去的文檔再看時竟然一路都比較順暢，一口氣看完大部。看完大部後，思路清晰了，知道理解LDA，可以分為下述5個步驟：

1. 一個函數：gamma函數
2. 四個分佈：二項分佈、多項分佈、beta分佈、Dirichlet分佈
3. 一個概念和一個理念：共軛先驗和貝葉斯框架
4. 兩個模型：pLSA、LDA（在本文第4 部分闡述）
5. 一個採樣：Gibbs採樣

    本文便按照上述5個步驟來闡述，希望讀者看完本文後，能對LDA有個儘量清晰完整的瞭解。同時，本文基於鄒講LDA的PPT、rickjin的LDA數學八卦及其它參考資料寫就，可以定義為一篇學習筆記或課程筆記，當然，後續不斷加入了很多自己的理解。若有任何問題，歡迎隨時於本文評論下指出，thanks。

 

1 gamma函數

1.0 整體把握LDA

    關於LDA有兩種含義，一種是線性判別分析（Linear Discriminant Analysis），一種是概率主題模型：隱含狄利克雷分佈（Latent Dirichlet Allocation，簡稱LDA），本文講後者。

    另外，我先簡單説下LDA的整體思想，不然我怕你看了半天，鋪了太長的前奏，卻依然因沒見到LDA的影子而顯得“心浮氣躁”，導致不想再繼續看下去。所以，先給你吃一顆定心丸，明白整體框架後，咱們再一步步抽絲剝繭，展開來論述。

    按照wiki上的介紹，LDA由Blei, David M.、Ng, Andrew Y.、Jordan於2003年提出，是一種主題模型，它可以將文檔集 中每篇文檔的主題以概率分佈的形式給出，從而通過分析一些文檔抽取出它們的主題（分佈）出來後，便可以根據主題（分佈）進行主題聚類或文本分類。同時，它是一種典型的詞袋模型，即一篇文檔是由一組詞構成，詞與詞之間沒有先後順序的關係。

    此外，一篇文檔可以包含多個主題，文檔中每一個詞都由其中的一個主題生成。

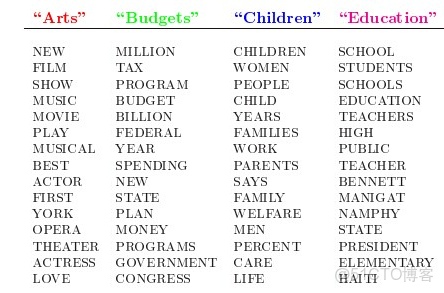
    人類是怎麼生成文檔的呢？LDA的這三位作者在原始論文中給了一個簡單的例子。比如假設事先給定了這幾個主題：Arts、Budgets、Children、Education，然後通過學習訓練，獲取每個主題Topic對應的詞語。如下圖所示：

 

    然後以一定的概率選取上述某個主題，再以一定的概率選取那個主題下的某個單詞，不斷的重複這兩步，最終生成如下圖所示的一篇文章（其中不同顏色的詞語分別對應上圖中不同主題下的詞）：

 

   而當我們看到一篇文章後，往往喜歡推測這篇文章是如何生成的，我們可能會認為作者先確定這篇文章的幾個主題，然後圍繞這幾個主題遣詞造句，表達成文。

    LDA就是要幹這事：根據給定的一篇文檔，推測其主題分佈。

    通俗來説，可以假定認為人類是根據上述文檔生成過程寫成了各種各樣的文章，現在某小撮人想讓計算機利用LDA幹一件事：你計算機給我推測分析網絡上各篇文章分別都寫了些啥主題，且各篇文章中各個主題出現的概率大小（主題分佈）是啥。

    然，就是這麼一個看似普通的LDA，一度嚇退了不少想深入探究其內部原理的初學者。難在哪呢，難就難在LDA內部涉及到的數學知識點太多了。

    在LDA模型中，一篇文檔生成的方式如下：

• 從狄利克雷分佈中取樣生成文檔 i 的主題分佈
• 從主題的多項式分佈中取樣生成文檔i第 j 個詞的主題
• 從狄利克雷分佈中取樣生成主題對應的詞語分佈
• 從詞語的多項式分佈中採樣最終生成詞語

    其中，類似Beta分佈是二項式分佈的共軛先驗概率分佈，而狄利克雷分佈（Dirichlet分佈）是多項式分佈的共軛先驗概率分佈。

    此外，LDA的圖模型結構如下圖所示（類似貝葉斯網絡結構）：

    恩，不錯，短短6句話整體概括了整個LDA的主體思想！但也就是上面短短6句話，卻接連不斷或重複出現了二項分佈、多項式分佈、beta分佈、狄利克雷分佈（Dirichlet分佈）、共軛先驗概率分佈、取樣，那麼請問，這些都是啥呢？

    這裏先簡單解釋下二項分佈、多項分佈、beta分佈、Dirichlet 分佈這4個分佈。

•  二項分佈（Binomial distribution）。

    二項分佈是從伯努利分佈推進的。伯努利分佈，又稱兩點分佈或0-1分佈，是一個離散型的隨機分佈，其中的隨機變量只有兩類取值，非正即負{+，-}。而二項分佈即重複n次的伯努利試驗，記為 

。簡言之，只做一次實驗，是伯努利分佈，重複做了n次，是二項分佈。二項分佈的概率密度函數為：

 

 

    對於k = 0, 1, 2, ..., n，其中的

 

是二項式係數（這就是二項分佈的名稱的由來），又記為

。回想起高中所學的那丁點概率知識了麼：想必你當年一定死記過這個二項式係數

就是

.

 

• 多項分佈，是二項分佈擴展到多維的情況。

    多項分佈是指單次試驗中的隨機變量的取值不再是0-1的，而是有多種離散值可能（1,2,3...,k）。比如投擲6個面的骰子實驗，N次實驗結果服從K=6的多項分佈。其中

 

     多項分佈的概率密度函數為：

• Beta分佈，二項分佈的共軛先驗分佈。

    給定參數

和

，取值範圍為[0,1]的隨機變量 x 的概率密度函數：

    其中：

，

。 

   注：

便是所謂的gamma函數，下文會具體闡述。

• Dirichlet分佈，是beta分佈在高維度上的推廣。

    Dirichlet分佈的的密度函數形式跟beta分佈的密度函數如出一轍：

    其中

    至此，我們可以看到二項分佈和多項分佈很相似，Beta分佈和Dirichlet 分佈很相似，而至於“Beta分佈是二項式分佈的共軛先驗概率分佈，而狄利克雷分佈（Dirichlet分佈）是多項式分佈的共軛先驗概率分佈”這點在下文中説明。

    OK，接下來，咱們就按照本文開頭所説的思路：“一個函數：gamma函數，四個分佈：二項分佈、多項分佈、beta分佈、Dirichlet分佈，外加一個概念和一個理念：共軛先驗和貝葉斯框架，兩個模型：pLSA、LDA（文檔-主題，主題-詞語），一個採樣：Gibbs採樣”一步步詳細闡述，爭取給讀者一個儘量清晰完整的LDA。

    （當然，如果你不想深究背後的細節原理，只想整體把握LDA的主體思想，可直接跳到本文第4 部分，看完第4部分後，若還是想深究背後的細節原理，可再回到此處開始看）

 

 

1.1 gamma函數

    咱們先來考慮一個問題（此問題1包括下文的問題2-問題4皆取材自LDA數學八卦）：

 

2. 問題1 隨機變量



3. 
   
5. 把這n 個隨機變量排序後得到順序統計量



6. 
   
8. 然後請問



9. 的分佈是什麼。

    為解決這個問題，可以嘗試計算

落在區間[x,x+Δx]的概率。即求下述式子的值：

 

    首先，把 [0,1] 區間分成三段 [0,x)，[x,x+Δx]，(x+Δx,1]，然後考慮下簡單的情形：即假設n 個數中只有1個落在了區間 [x,x+Δx]內，由於這個區間內的數X(k)是第k大的，所以[0,x)中應該有 k−1 個數，(x+Δx,1] 這個區間中應該有n−k 個數。如下圖所示：

    從而問題轉換為下述事件E：

 

    對於上述事件E，有：

    其中，o(Δx)表示Δx的高階無窮小。顯然，由於不同的排列組合，即n個數中有一個落在 [x,x+Δx]區間的有n種取法，餘下n−1個數中有k−1個落在[0,x)的有

種組合，所以和事件E等價的事件一共有

個。

 

    如果有2個數落在區間[x,x+Δx]呢？如下圖所示：

    類似於事件E，對於2個數落在區間[x,x+Δx]的事件E’：

    有：

   從上述的事件E、事件E‘中，可以看出，只要落在[x,x+Δx]內的數字超過一個，則對應的事件的概率就是 o(Δx)。於是乎有：

    從而得到

的概率密度函數

為：

    至此，本節開頭提出的問題得到解決。然仔細觀察

的概率密度函數，發現式子的最終結果有階乘，聯想到階乘在實數上的推廣

函數：

    兩者結合是否會產生奇妙的效果呢？考慮到

具有如下性質：

 

    故將代入到

的概率密度函數

中，可得：

    然後取

，

，轉換

得到：

    如果熟悉beta分佈的朋友，可能會驚呼：哇，竟然推出了beta分佈！

 

 

2 beta分佈

2.1 beta分佈

    在概率論中，beta是指一組定義在

區間的連續概率分佈，有兩個參數

和

，且

。

 

 

    beta分佈的概率密度函數是：

    其中的

便是

函數：

    隨機變量X服從參數為的beta分佈通常寫作：

。

2.2 Beta-Binomial 共軛

    回顧下1.1節開頭所提出的問題：“問題1 隨機變量

，把這n 個隨機變量排序後得到順序統計量

，然後請問

的分佈是什麼。” 如果，咱們要在這個問題的基礎上增加一些觀測數據，變成問題2：

• 

• ，對應的順序統計量是



• ，需要猜測



• ；

• 

• ， 



• 中有



• 個比p小，



• 個比



• 大；
• 那麼，請問



• 的分佈是什麼。

    根據“Yi中有

個比

小，

個比

大”，換言之，Yi中有

個比

小，

個比

大，所以

是

中第

大的數。    根據1.1節最終得到的結論“只要落在[x,x+Δx]內的數字超過一個，則對應的事件的概率就是 o(Δx)”，繼而推出事件服從beta分佈，從而可知

的概率密度函數為：

   

    熟悉貝葉斯方法（不熟悉的沒事，參見此文第一部分）的朋友心裏估計又犯“嘀咕”了，這不就是貝葉斯式的思考過程麼？

2. 為了猜測



3. ，在獲得一定的觀測數據前，我們對



4. 的認知是：



5. ，此稱為



6. 的先驗分佈；
8. 然後為了獲得這個結果“ 



9. 中有



10. 個比p小，



11. 個比



12. 大”，針對



13. 是做了



14. 次貝努利實驗，所以



15. 服從二項分佈



16. ；
18. 在給定了來自數據提供的



19. 的知識後，



20. 的後驗分佈變為



21. 。

• 先驗分佈



•  + 樣本信息



•  



•  後驗分佈



• 
  

    上述思考模式意味着，新觀察到的樣本信息將修正人們以前對事物的認知。換言之，在得到新的樣本信息之前，人們對

的認知是先驗分佈

，在得到新的樣本信息

後，人們對

的認知為

。

    類比到現在這個問題上，我們也可以試着寫下：

    其中

對應的是二項分佈

的計數。    更一般的，對於非負實數

和

，我們有如下關係

 

    針對於這種觀測到的數據符合二項分佈，參數的先驗分佈和後驗分佈都是Beta分佈的情況，就是Beta-Binomial共軛。換言之，Beta分佈是二項式分佈的共軛先驗概率分佈。

    二項分佈和Beta分佈是共軛分佈意味着，如果我們為二項分佈的參數p選取的先驗分佈是Beta分佈，那麼以p為參數的二項分佈用貝葉斯估計得到的後驗分佈仍然服從Beta分佈。

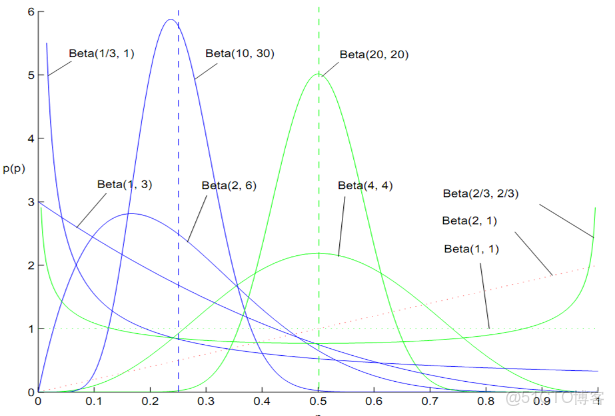
    此外，如何理解參數

和

所表達的意義呢？

、

可以認為形狀參數，通俗但不嚴格的理解是，

和

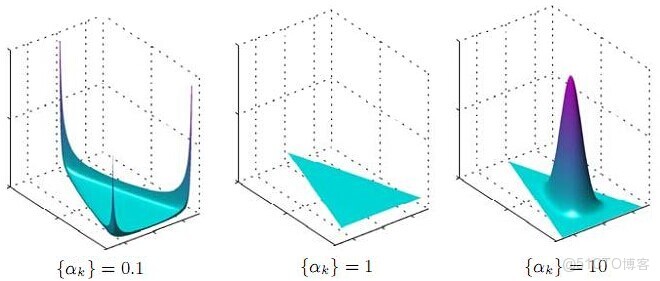
共同控制Beta分佈的函數“長的樣子”：形狀千奇百怪，高低胖瘦，如下圖所示：

2.3 共軛先驗分佈

    什麼又是共軛呢？軛的意思是束縛、控制，共軛從字面上理解，則是共同約束，或互相約束。

    在貝葉斯概率理論中，如果後驗概率P(θ|x)和先驗概率p(θ)滿足同樣的分佈律，那麼，先驗分佈和後驗分佈被叫做共軛分佈，同時，先驗分佈叫做似然函數的共軛先驗分佈。

    比如，某觀測數據服從概率分佈P(θ)時，當觀測到新的X數據時，我們一般會遇到如下問題：

• 可否根據新觀測數據X，更新參數θ？
• 根據新觀測數據可以在多大程度上改變參數θ，即

• 當重新估計θ的時候，給出新參數值θ的新概率分佈，即P(θ|x)。

    事實上，根據根據貝葉斯公式可知：

    其中，P(x|θ)表示以預估θ為參數的x概率分佈，可以直接求得，P(θ)是已有原始的θ概率分佈。
    所以，如果我們選取P(x|θ)的共軛先驗作為P(θ)的分佈，那麼P(x|θ)乘以P(θ)，然後歸一化的結果P(θ|x)跟和P(θ)的形式一樣。換句話説，先驗分佈是P(θ)，後驗分佈是P(θ|x)，先驗分佈跟後驗分佈同屬於一個分佈族，故稱該分佈族是θ的共軛先驗分佈（族）。

    舉個例子。投擲一個非均勻硬幣，可以使用參數為θ的伯努利模型，θ為硬幣為正面的概率，那麼結果x的分佈形式為：

    其共軛先驗為beta分佈，具有兩個參數

和

，稱為超參數（hyperparameters）。且這兩個參數決定了θ參數，其Beta分佈形式為

    然後計算後驗概率

    歸一化這個等式後會得到另一個Beta分佈，從而證明了Beta分佈確實是伯努利分佈的共軛先驗分佈。

2.4 從beta分佈推廣到Dirichlet 分佈

    接下來，咱們來考察beta分佈的一個性質。

    如果

，則有：

    注意到上式最後結果的右邊積分

    其類似於概率分佈

，而對於這個分佈有

    從而求得

    的結果為

    最後將此結果帶入

的計算式，得到：

    最後的這個結果意味着對於Beta 分佈的隨機變量，其均值（期望）可以用

來估計。此外，狄利克雷Dirichlet 分佈也有類似的結論，即如果

，同樣可以證明有下述結論成立：

    那什麼是Dirichlet 分佈呢？簡單的理解Dirichlet 分佈就是一組連續多變量概率分佈，是多變量普遍化的beta分佈。為了紀念德國數學家約翰·彼得·古斯塔夫·勒熱納·狄利克雷（Peter Gustav Lejeune Dirichlet）而命名。狄利克雷分佈常作為貝葉斯統計的先驗概率。

3 Dirichlet 分佈

3.1 Dirichlet 分佈

    根據wikipedia上的介紹，維度K ≥ 2（x1,x2…xK-1維，共K個）的狄利克雷分佈在參數α1, ..., αK > 0上、基於歐幾里得空間RK-1裏的勒貝格測度有個概率密度函數，定義為：

    其中，

相當於是多項beta函數

    且

    此外，x1+x2+…+xK-1+xK=1，x1,x2…xK-1>0，且在(K-1)維的單純形上，其他區域的概率密度為0。

    當然，也可以如下定義Dirichlet 分佈

    其中的

稱為Dirichlet 分佈的歸一化係數：

    且根據Dirichlet分佈的積分為1（概率的基本性質），可以得到：

3.2 Dirichlet-Multinomial 共軛

    下面，在2.2節問題2的基礎上繼續深入，引出問題3。

• 

• ，
• 排序後對應的順序統計量



• ,
• 問



• 的聯合分佈是什麼？

    為了簡化計算，取x3滿足x1+x2+x3=1,但只有x1,x2是變量，如下圖所示：

    從而有：

    繼而得到於是我們得到

的聯合分佈為：

    觀察上述式子的最終結果，可以看出上面這個分佈其實就是3維形式的 Dirichlet 分佈

    令

，於是分佈密度可以寫為

    這個就是一般形式的3維 Dirichlet 分佈，即便

延拓到非負實數集合，以上概率分佈也是良定義的。

    將Dirichlet分佈的概率密度函數取對數，繪製對稱Dirichlet分佈的圖像如下圖所示（截取自wikipedia上）：

上圖中，取K=3，也就是有兩個獨立參數x1,x2，分別對應圖中的兩個座標軸，第三個參數始終滿足x3=1-x1-x2且α1=α2=α3=α，圖中反映的是參數α從α=(0.3, 0.3, 0.3)變化到(2.0, 2.0, 2.0)時的概率對數值的變化情況。

    為了論證Dirichlet分佈是多項式分佈的共軛先驗概率分佈，下面咱們繼續在上述問題3的基礎上再進一步，提出問題4。

2. 問題4  



3. ，排序後對應的順序統計量



4. 
   
6. 令



7. ,



8. ,



9. （此處的p3非變量，只是為了表達方便），現在要猜測



10. ；

11. 

12. ，Yi中落到



13. ，



14. ，



15.  三個區間的個數分別為 m1,m2,m3，m=m1+m2+m3；
17.  問後驗分佈



18. 的分佈是什麼。

   為了方便討論，記

，及

，根據已知條件“

，Yi中落到

，

，

 三個區間的個數分別為 m1,m2”，可得

、

分別是這m+n個數中第

大、第

大的數。於是，後驗分佈

應該為

，即一般化的形式表示為：

。

    同樣的，按照貝葉斯推理的邏輯，可將上述過程整理如下：

2.  我們要猜測參數



3. ，其先驗分佈為



4. ；
6.  數據Yi落到三個區間



7. ，



8. ，



9.  的個數分別為



10. ，所以



11. 服從多項分佈



12. 
    
14.  在給定了來自數據提供的知識



15. 後，



16. 的後驗分佈變為



17. 
    

    上述貝葉斯分析過程的直觀表述為：

    令

，可把

從整數集合延拓到實數集合，從而得到更一般的表達式如下：

    針對於這種觀測到的數據符合多項分佈，參數的先驗分佈和後驗分佈都是Dirichlet 分佈的情況，就是Dirichlet-Multinomial 共軛。換言之，至此已經證明了Dirichlet分佈的確就是多項式分佈的共軛先驗概率分佈。

    意味着，如果我們為多項分佈的參數p選取的先驗分佈是Dirichlet分佈，那麼以p為參數的多項分佈用貝葉斯估計得到的後驗分佈仍然服從Dirichlet分佈。

    進一步，一般形式的Dirichlet 分佈定義如下：

    而對於給定的

和

，其多項分佈為：

    結論是：Dirichlet分佈

和多項分佈

是共軛關係。

4 主題模型LDA

        在開始下面的旅程之前，先來總結下我們目前所得到的最主要的幾個收穫：

• 通過上文的第2.2節，我們知道beta分佈是二項式分佈的共軛先驗概率分佈：
•  “對於非負實數



• 和



• ，我們有如下關係

    其中

對應的是二項分佈

的計數。針對於這種觀測到的數據符合二項分佈，參數的先驗分佈和後驗分佈都是Beta分佈的情況，就是Beta-Binomial 共軛。”

• 通過上文的3.2節，我們知道狄利克雷分佈（Dirichlet分佈）是多項式分佈的共軛先驗概率分佈：
• “ 把



• 從整數集合延拓到實數集合，從而得到更一般的表達式如下：

    針對於這種觀測到的數據符合多項分佈，參數的先驗分佈和後驗分佈都是Dirichlet 分佈的情況，就是 Dirichlet-Multinomial 共軛。 ”

• 以及貝葉斯派思考問題的固定模式：

  • 先驗分佈

  

  •  + 樣本信息

  

  

  •  後驗分佈

  

  • 
    

  
  

•     上述思考模式意味着，新觀察到的樣本信息將修正人們以前對事物的認知。換言之，在得到新的樣本信息之前，人們對



• 的認知是先驗分佈



• ，在得到新的樣本信息



• 後，人們對



• 的認知為



• 。
• 順便提下頻率派與貝葉斯派各自不同的思考方式：
• 頻率派把需要推斷的參數θ看做是固定的未知常數，即概率



• 雖然是未知的，但最起碼是確定的一個值，同時，樣本X 是隨機的，所以頻率派重點研究樣本空間，大部分的概率計算都是針對樣本X 的分佈；
• 而貝葉斯派的觀點則截然相反，他們認為待估計的參數



• 是隨機變量，服從一定的分佈，而樣本X 是固定的，由於樣本是固定的，所以他們重點研究的是參數



• 的分佈。

    OK，在殺到終極boss——LDA模型之前，再循序漸進理解基礎模型：Unigram model、mixture of unigrams model，以及跟LDA最為接近的pLSA模型。

   為了方便描述，首先定義一些變量：

• 

• 表示詞，



• 表示所有單詞的個數（固定值）

• 

• 表示主題，



• 是主題的個數（預先給定，固定值）

• 

• 表示語料庫，其中的



• 是語料庫中的文檔數（固定值）

• 

• 表示文檔，其中的



• 表示一個文檔中的詞數（隨機變量）

4.1 各個基礎模型

4.1.1 Unigram model

    對於文檔

，用

表示詞

的先驗概率，生成文檔

的概率為：

    其圖模型為（圖中被塗色的w表示可觀測變量，N表示一篇文檔中總共N個單詞，M表示M篇文檔）：

    或為：

    unigram model假設文本中的詞服從Multinomial分佈，而我們已經知道Multinomial分佈的先驗分佈為Dirichlet分佈。

    上圖中的

表示在文本中觀察到的第n個詞，n∈[1,N]表示該文本中一共有N個單詞。加上方框表示重複，即一共有N個這樣的隨機變量

。其中，p和α是隱含未知變量：

• p是詞服從的Multinomial分佈的參數
• α是Dirichlet分佈（即Multinomial分佈的先驗分佈）的參數。

    一般α由經驗事先給定，p由觀察到的文本中出現的詞學習得到，表示文本中出現每個詞的概率。

4.1.2 Mixture of unigrams model

    該模型的生成過程是：給某個文檔先選擇一個主題

，再根據該主題生成文檔，該文檔中的所有詞都來自一個主題。假設主題有

，生成文檔

的概率為：

    其圖模型為（圖中被塗色的w表示可觀測變量，未被塗色的z表示未知的隱變量，N表示一篇文檔中總共N個單詞，M表示M篇文檔）：

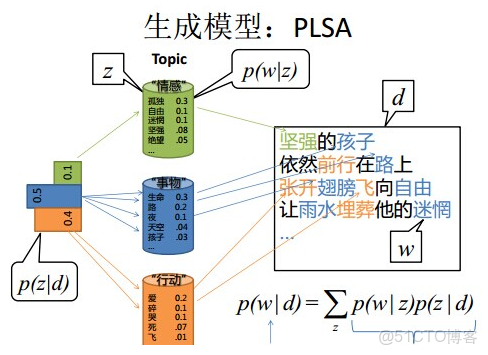
4.2 PLSA模型

    啊哈，長征兩萬五，經過前面這麼長的鋪墊，終於快要接近LDA模型了！因為跟LDA模型最為接近的便是下面要闡述的這個pLSA模型，理解了pLSA模型後，到LDA模型也就一步之遙——給pLSA加上貝葉斯框架，便是LDA。

4.2.1 pLSA模型下生成文檔

OK，在上面的Mixture of unigrams model中，我們假定一篇文檔只有一個主題生成，可 實際中，一篇文章往往有多個主題，只是這多個主題各自在文檔中出現的概率大小不一樣。比如介紹一個國家的文檔中，往往會分別從教育、經濟、交通等多個主題進行介紹。那麼在pLSA中，文檔是怎樣被生成的呢？

    假設你要寫M篇文檔，由於一篇文檔由各個不同的詞組成，所以你需要確定每篇文檔裏每個位置上的詞。

    再假定你一共有K個可選的主題，有V個可選的詞，咱們來玩一個扔骰子的遊戲。

• 1. 假設你每寫一篇文檔會製作一顆K面的“文檔-主題”骰子（扔此骰子能得到K個主題中的任意一個），和K個V面的“主題-詞項” 骰子（每個骰子對應一個主題，K個骰子對應之前的K個主題，且骰子的每一面對應要選擇的詞項，V個面對應着V個可選的詞）。
• 比如可令K=3，即製作1個含有3個主題的“文檔-主題”骰子，這3個主題可以是：教育、經濟、交通。然後令V = 3，製作3個有着3面的“主題-詞項”骰子，其中，教育主題骰子的3個面上的詞可以是：大學、老師、課程，經濟主題骰子的3個面上的詞可以是：市場、企業、金融，交通主題骰子的3個面上的詞可以是：高鐵、汽車、飛機。
• 2. 每寫一個詞，先扔該“文檔-主題”骰子選擇主題，得到主題的結果後，使用和主題結果對應的那顆“主題-詞項”骰子，扔該骰子選擇要寫的詞。
• 先扔“文檔-主題”的骰子，假設（以一定的概率）得到的主題是教育，所以下一步便是扔教育主題篩子，（以一定的概率）得到教育主題篩子對應的某個詞：大學。
• 上面這個投骰子產生詞的過程簡化下便是：“先以一定的概率選取主題，再以一定的概率選取詞”。事實上，一開始可供選擇的主題有3個：教育、經濟、交通，那為何偏偏選取教育這個主題呢？其實是隨機選取的，只是這個隨機遵循一定的概率分佈。比如可能選取教育主題的概率是0.5，選取經濟主題的概率是0.3，選取交通主題的概率是0.2，那麼這3個主題的概率分佈便是{教育：0.5，經濟：0.3，交通：0.2}，我們把各個主題z在文檔d中出現的概率分佈稱之為主題分佈，且是一個多項分佈。
• 同樣的，從主題分佈中隨機抽取出教育主題後，依然面對着3個詞：大學、老師、課程，這3個詞都可能被選中，但它們被選中的概率也是不一樣的。比如大學這個詞被選中的概率是0.5，老師這個詞被選中的概率是0.3，課程被選中的概率是0.2，那麼這3個詞的概率分佈便是{大學：0.5，老師：0.3，課程：0.2}，我們把各個詞語w在主題z下出現的概率分佈稱之為詞分佈，這個詞分佈也是一個多項分佈。
• 所以，選主題和選詞都是兩個隨機的過程，先從主題分佈{教育：0.5，經濟：0.3，交通：0.2}中抽取出主題：教育，然後從該主題對應的詞分佈{大學：0.5，老師：0.3，課程：0.2}中抽取出詞：大學。

• 3. 最後，你不停的重複扔“文檔-主題”骰子和”主題-詞項“骰子，重複N次（產生N個詞），完成一篇文檔，重複這產生一篇文檔的方法M次，則完成M篇文檔。

    上述過程抽象出來即是PLSA的文檔生成模型。在這個過程中，我們並未關注詞和詞之間的出現順序，所以pLSA是一種詞袋方法。具體説來，該模型假設一組共現(co-occurrence)詞項關聯着一個隱含的主題類別

。同時定義：

• 

• 表示海量文檔中某篇文檔被選中的概率。

• 

• 表示詞



• 在給定文檔



• 中出現的概率。
• 怎麼計算得到呢？針對海量文檔，對所有文檔進行分詞後，得到一個詞彙列表，這樣每篇文檔就是一個詞語的集合。對於每個詞語，用它在文檔中出現的次數除以文檔中詞語總的數目便是它在文檔中出現的概率



• 。

• 

• 表示具體某個主題



• 在給定文檔



• 下出現的概率。

• 

• 表示具體某個詞



• 在給定主題



• 下出現的概率，與主題關係越密切的詞，其條件概率



• 越大。

    利用上述的第1、3、4個概率，我們便可以按照如下的步驟得到“文檔-詞項”的生成模型：

2. 按照概率



3. 選擇一篇文檔



4. 
   
6. 選定文檔



7. 後，從主題分佈中按照概率



8. 選擇一個隱含的主題類別



9. 
   
11. 選定



12. 後，從詞分佈中按照概率



13. 選擇一個詞



14. 
    

    所以pLSA中生成文檔的整個過程便是選定文檔生成主題，確定主題生成詞。

4.2.1 根據文檔反推其主題分佈

    反過來，既然文檔已經產生，那麼如何根據已經產生好的文檔反推其主題呢？這個利用看到的文檔推斷其隱藏的主題（分佈）的過程（其實也就是產生文檔的逆過程），便是主題建模的目的：自動地發現文檔集中的主題（分佈）。

    換言之，人類根據文檔生成模型寫成了各類文章，然後丟給了計算機，相當於計算機看到的是一篇篇已經寫好的文章。現在計算機需要根據一篇篇文章中看到的一系列詞歸納出當篇文章的主題，進而得出各個主題各自不同的出現概率：主題分佈。即文檔d和單詞w是可被觀察到的，但主題z卻是隱藏的。

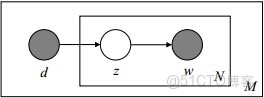
    如下圖所示（圖中被塗色的d、w表示可觀測變量，未被塗色的z表示未知的隱變量，N表示一篇文檔中總共N個單詞，M表示M篇文檔）：

    上圖中，文檔d和詞w是我們得到的樣本（樣本隨機，參數雖未知但固定，所以pLSA屬於頻率派思想。區別於下文要介紹的LDA中：樣本固定，參數未知但不固定，是個隨機變量，服從一定的分佈，所以LDA屬於貝葉斯派思想），可觀測得到，所以對於任意一篇文檔，其

是已知的。

    從而可以根據大量已知的文檔-詞項信息

，訓練出文檔-主題

和主題-詞項

，如下公式所示：

    故得到文檔中每個詞的生成概率為：

    由於

可事先計算求出，而

和

未知，所以

就是我們要估計的參數（值），通俗點説，就是要最大化這個θ。

    用什麼方法進行估計呢，常用的參數估計方法有極大似然估計MLE、最大後驗證估計MAP、貝葉斯估計等等。因為該待估計的參數中含有隱變量z，所以我們可以考慮EM算法。

4.2.1.1 EM算法的簡單介紹

    EM算法，全稱為Expectation-maximization algorithm，為期望最大算法，其基本思想是：首先隨機選取一個值去初始化待估計的值

，然後不斷迭代尋找更優的

使得其似然函數likelihood 

比原來的

要大。換言之，假定現在得到了

，想求

，使得

    EM的關鍵便是要找到

的一個下界

（注：

，其中，X表示已經觀察到的隨機變量），然後不斷最大化這個下界，通過不斷求解下界

的極大化，從而逼近要求解的似然函數

。

    所以EM算法的一般步驟為：

• 1. 隨機選取或者根據先驗知識初始化



• ；
• 2. 不斷迭代下述兩步
• ①給出當前的參數估計



• ，計算似然函數



• 的下界



• 
  
• ②重新估計參數θ，即求



• ，使得



• 
  
• 3. 上述第二步後，如果



• 收斂（即



• 收斂）則退出算法，否則繼續回到第二步。

    上述過程好比在二維平面上，有兩條不相交的曲線，一條曲線在上（簡稱上曲線

），一條曲線在下（簡稱下曲線

），下曲線為上曲線的下界。現在對上曲線未知，只已知下曲線，為了求解上曲線的最高點，我們試着不斷增大下曲線，使得下曲線不斷逼近上曲線，下曲線在某一個點達到局部最大值並與上曲線在這點的值相等，記錄下這個值，然後繼續增大下曲線，尋找下曲線上與上曲線上相等的值，迭代到

收斂（即

收斂）停止，從而利用當前下曲線上的局部最大值當作上曲線的全局最大值（換言之，EM算法不保證一定能找到全局最優值）。如下圖所示：

    以下是詳細介紹。

    假定有訓練集

，包含m個獨立樣本，希望從中找到該組數據的模型p(x,z)的參數。   

    然後通過極大似然估計建立目標函數--對數似然函數：

    這裏，z是隱隨機變量，直接找到參數的估計是很困難的。我們的策略是建立的下界，並且求該下界的最大值；重複這個過程，直到收斂到局部最大值。

    令Qi是z的某一個分佈，Qi≥0，且結合Jensen不等式，有：

    為了尋找儘量緊的下界，我們可以讓使上述等號成立，而若要讓等號成立的條件則是：

    換言之，有以下式子成立：

，且由於有：

    所以可得：

    最終得到EM算法的整體框架如下：

    OK，EM算法還會在本博客後面的博文中具體闡述。接下來，回到pLSA參數的估計問題上。

4.2.1.2 EM算法估計pLSA的兩未知參數

    首先嚐試從矩陣的角度來描述待估計的兩個未知變量

和

。

• 假定用



• 表示詞表



• 在主題



• 上的一個多項分佈，則



• 可以表示成一個向量，每個元素



• 表示詞項



• 出現在主題



• 中的概率，即

• 用



• 表示所有主題



• 在文檔



• 上的一個多項分佈，則



• 可以表示成一個向量，每個元素



• 表示主題



• 出現在文檔



• 中的概率，即

    這樣，巧妙的把

和

轉換成了兩個矩陣。換言之，最終我們要求解的參數是這兩個矩陣：

    由於詞和詞之間是相互獨立的，所以整篇文檔N個詞的分佈為：

    再由於文檔和文檔之間也是相互獨立的，所以整個語料庫中詞的分佈為（整個語料庫M篇文檔，每篇文檔N個詞）：

    其中，

表示詞項

在文檔

中的詞頻，

表示文檔di中詞的總數，顯然有

。

    從而得到整個語料庫的詞分佈的對數似然函數（下述公式中有個小錯誤，正確的應該是：N為M，M為N）：

    現在，我們需要最大化上述這個對數似然函數來求解參數

和

。對於這種含有隱變量的最大似然估計，可以使用EM算法。EM算法，分為兩個步驟：先E-step，後M-step。

• E-step：假定參數已知，計算此時隱變量的後驗概率。

    利用貝葉斯法則，可以得到：

• M-step：帶入隱變量的後驗概率，最大化樣本分佈的對數似然函數，求解相應的參數。

    觀察之前得到的對數似然函數

的結果，由於文檔長度

可以單獨計算，所以去掉它不影響最大化似然函數。此外，根據E-step的計算結果，把 

代入

，於是我們只要最大化下面這個函數 

 即可（下述公式中有個小錯誤，正確的應該是：N為M，M為N）：

    這是一個多元函數求極值問題，並且已知有如下約束條件（下述公式中有個小錯誤，正確的應該是：M為N）：

    熟悉凸優化的朋友應該知道，一般處理這種帶有約束條件的極值問題，常用的方法便是拉格朗日乘數法，即通過引入拉格朗日乘子將約束條件和多元（目標）函數融合到一起，轉化為無約束條件的極值問題。

    這裏我們引入兩個拉格朗日乘子

和

，從而寫出拉格朗日函數（下述公式中有個小錯誤，正確的應該是：N為M，M為N）：

    因為我們要求解的參數是

和

，所以分別對

和

求偏導，然後令偏導結果等於0，得到（下述公式中有個小錯誤，正確的應該是：N為M，M為N）：

    消去拉格朗日乘子，最終可估計出參數

和

（下述公式中有個小錯誤，正確的應該是：N為M，M為N）：

    綜上，在pLSA中：

2. 由於



3. 和



4. 未知，所以我們用EM算法去估計



5. 這個參數的值。
7. 而後，用



8. 表示詞項



9. 出現在主題



10. 中的概率，即
11. ，用



12. 表示主題



13. 出現在文檔



14. 中的概率，即
15. ，從而把



16. 轉換成了“主題-詞項”矩陣Φ（主題生成詞），把



17. 轉換成了“文檔-主題”矩陣Θ（文檔生成主題）。
19. 最終求解出



20. 、



21. 。

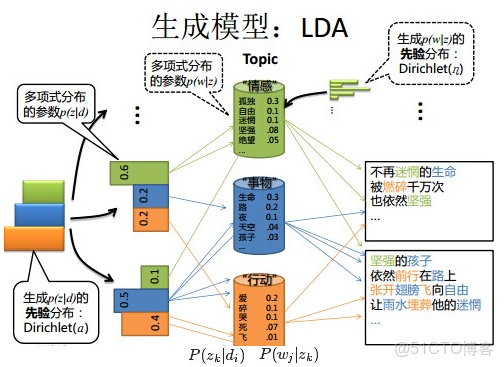
4.3 LDA模型

    事實上，理解了pLSA模型，也就差不多快理解了LDA模型，因為LDA就是在pLSA的基礎上加層貝葉斯框架，即LDA就是pLSA的貝葉斯版本（正因為LDA被貝葉斯化了，所以才需要考慮歷史先驗知識，才加的兩個先驗參數）。

4.3.1 pLSA跟LDA的對比：生成文檔與參數估計

    在pLSA模型中，我們按照如下的步驟得到“文檔-詞項”的生成模型：

2. 按照概率



3. 選擇一篇文檔



4. 
   
6. 選定文檔



7. 後，確定文章的主題分佈
9. 從主題分佈中按照概率



10. 選擇一個隱含的主題類別



11. 
    
13. 選定



14. 後，確定主題下的詞分佈
16. 從詞分佈中按照概率



17. 選擇一個詞



18.  ”

    下面，咱們對比下本文開頭所述的LDA模型中一篇文檔生成的方式是怎樣的：

2. 按照先驗概率



3. 選擇一篇文檔



4. 
   
6. 從狄利克雷分佈（即Dirichlet分佈）



7. 中取樣生成文檔 



8. 的主題分佈



9. ，換言之，主題分佈



10. 由超參數為



11. 的Dirichlet分佈生成
13. 從主題的多項式分佈



14. 中取樣生成文檔



15. 第 j 個詞的主題



16. 
    
18. 從狄利克雷分佈（即Dirichlet分佈）



19. 中取樣生成主題



20. 對應的詞語分佈



21. ，換言之，詞語分佈



22. 由參數為



23. 的Dirichlet分佈生成
25. 從詞語的多項式分佈



26. 中採樣最終生成詞語



27.  ”

    從上面兩個過程可以看出，LDA在PLSA的基礎上，為主題分佈和詞分佈分別加了兩個Dirichlet先驗。

    繼續拿之前講解PLSA的例子進行具體説明。如前所述，在PLSA中，選主題和選詞都是兩個隨機的過程，先從主題分佈{教育：0.5，經濟：0.3，交通：0.2}中抽取出主題：教育，然後從該主題對應的詞分佈{大學：0.5，老師：0.3，課程：0.2}中抽取出詞：大學。

    而在LDA中，選主題和選詞依然都是兩個隨機的過程，依然可能是先從主題分佈{教育：0.5，經濟：0.3，交通：0.2}中抽取出主題：教育，然後再從該主題對應的詞分佈{大學：0.5，老師：0.3，課程：0.2}中抽取出詞：大學。

    那PLSA跟LDA的區別在於什麼地方呢？區別就在於：

• PLSA中，主題分佈和詞分佈是唯一確定的，能明確的指出主題分佈可能就是{教育：0.5，經濟：0.3，交通：0.2}，詞分佈可能就是{大學：0.5，老師：0.3，課程：0.2}。
• 但在LDA中，主題分佈和詞分佈不再唯一確定不變，即無法確切給出。例如主題分佈可能是{教育：0.5，經濟：0.3，交通：0.2}，也可能是{教育：0.6，經濟：0.2，交通：0.2}，到底是哪個我們不再確定（即不知道），因為它是隨機的可變化的。但再怎麼變化，也依然服從一定的分佈，即主題分佈跟詞分佈由Dirichlet先驗隨機確定。

   看到這，你可能凌亂了，你説面對多個主題或詞，各個主題或詞被抽中的概率不一樣，所以抽取主題或詞是隨機抽取，還好理解。但現在你説主題分佈和詞分佈本身也都是不確定的，這是怎麼回事？沒辦法，誰叫Blei等人“強行”給PLSA安了個貝葉斯框架呢，正因為LDA是PLSA的貝葉斯版本，所以主題分佈跟詞分佈本身由先驗知識隨機給定。

    進一步，你會發現：

• pLSA中，主題分佈和詞分佈確定後，以一定的概率（



• 、



• ）分別選取具體的主題和詞項，生成好文檔。而後根據生成好的文檔反推其主題分佈、詞分佈時，最終用EM算法（極大似然估計思想）求解出了兩個未知但固定的參數的值：



• （由



• 轉換而來）和



• （由



• 轉換而來）。
• 文檔d產生主題z的概率，主題z產生單詞w的概率都是兩個固定的值。
• 舉個文檔d產生主題z的例子。給定一篇文檔d，主題分佈是一定的，比如{ P(zi|d), i = 1,2,3 }可能就是{0.4,0.5,0.1}，表示z1、z2、z3，這3個主題被文檔d選中的概率都是個固定的值：P(z1|d) = 0.4、P(z2|d) = 0.5、P(z3|d) = 0.1，如下圖所示（圖截取自沈博PPT上）：

• 

• 但在貝葉斯框架下的LDA中，我們不再認為主題分佈（各個主題在文檔中出現的概率分佈）和詞分佈（各個詞語在某個主題下出現的概率分佈）是唯一確定的（而是隨機變量），而是有很多種可能。但一篇文檔總得對應一個主題分佈和一個詞分佈吧，怎麼辦呢？LDA為它們弄了兩個Dirichlet先驗參數，這個Dirichlet先驗為某篇文檔隨機抽取出某個主題分佈和詞分佈。
• 文檔d產生主題z（準確的説，其實是Dirichlet先驗為文檔d生成主題分佈Θ，然後根據主題分佈Θ產生主題z）的概率，主題z產生單詞w的概率都不再是某兩個確定的值，而是隨機變量。
• 還是再次舉下文檔d具體產生主題z的例子。給定一篇文檔d，現在有多個主題z1、z2、z3，它們的主題分佈{ P(zi|d), i = 1,2,3 }可能是{0.4,0.5,0.1}，也可能是{0.2,0.2,0.6}，即這些主題被d選中的概率都不再認為是確定的值，可能是P(z1|d) = 0.4、P(z2|d) = 0.5、P(z3|d) = 0.1，也有可能是P(z1|d) = 0.2、P(z2|d) = 0.2、P(z3|d) = 0.6等等，而主題分佈到底是哪個取值集合我們不確定（為什麼？這就是貝葉斯派的核心思想，把未知參數當作是隨機變量，不再認為是某一個確定的值），但其先驗分佈是dirichlet 分佈，所以可以從無窮多個主題分佈中按照dirichlet 先驗隨機抽取出某個主題分佈出來。如下圖所示（圖截取自沈博PPT上）：

 

    換言之，LDA在pLSA的基礎上給這兩參數（

、

）加了兩個先驗分佈的參數（貝葉斯化）：一個主題分佈的先驗分佈Dirichlet分佈

，和一個詞語分佈的先驗分佈Dirichlet分佈

。

    綜上，LDA真的只是pLSA的貝葉斯版本，文檔生成後，兩者都要根據文檔去推斷其主題分佈和詞語分佈（ 即兩者本質都是為了估計給定文檔生成主題，給定主題生成詞語的概率 ），只是用的參數推斷方法不同，在pLSA中用極大似然估計的思想去推斷兩未知的固定參數，而LDA則把這兩參數弄成隨機變量，且加入dirichlet先驗。

    所以，pLSA跟LDA的本質區別就在於它們去估計未知參數所採用的思想不同，前者用的是頻率派思想，後者用的是貝葉斯派思想。
    好比，我去一朋友家：

• 按照頻率派的思想，我估計他在家的概率是1/2，不在家的概率也是1/2，是個定值。
• 而按照貝葉斯派的思想，他在家不在家的概率不再認為是個定值1/2，而是隨機變量。比如按照我們的經驗（比如當天週末），猜測他在家的概率是0.6，但這個0.6不是説就是完全確定的，也有可能是0.7。如此，貝葉斯派沒法確切給出參數的確定值（0.3,0.4，0.6,0.7，0.8,0.9都有可能），但至少明白在哪個範圍或哪些取值（0.6,0.7，0.8,0.9）更有可能，哪個範圍或哪些取值（0.3,0.4） 不太可能。進一步，貝葉斯估計中，參數的多個估計值服從一定的先驗分佈，而後根據實踐獲得的數據（例如週末不斷跑他家），不斷修正之前的參數估計，從先驗分佈慢慢過渡到後驗分佈。

    OK，相信已經解釋清楚了。如果是在機器學習班上face-to-face，更好解釋和溝通。

4.3.2 LDA生成文檔過程的進一步理解

    上面説，LDA中，主題分佈 —— 比如{ P(zi), i =1,2,3 }等於{0.4,0.5,0.1}或{0.2,0.2,0.6} —— 是由dirichlet先驗給定的，不是根據文檔產生的。所以，LDA生成文檔的過程中，先從dirichlet先驗中“隨機”抽取出主題分佈，然後從主題分佈中“隨機”抽取出主題，最後從確定後的主題對應的詞分佈中“隨機”抽取出詞。

    那麼，dirichlet先驗到底是如何“隨機”抽取主題分佈的呢？

    事實上，從dirichlet分佈中隨機抽取主題分佈，這個過程不是完全隨機的。為了説清楚這個問題，咱們得回顧下dirichlet分佈。事實上，如果我們取3個事件的話，可以建立一個三維座標系，類似xyz三維座標系，這裏，我們把3個座標軸弄為p1、p2、p3，如下圖所示：

 在這個三維座標軸所劃分的空間裏，每一個座標點(p1,p2,p3)就對應着一個主題分佈，且某一個點(p1,p2,p3)的大小表示3個主題z1、z2、z3出現的概率大小（因為各個主題出現的概率和為1，所以p1+p2+p3 = 1，且p1、p2、p3這3個點最大取值為1）。比如(p1,p2,p3) = (0.4,0.5,0.1)便對應着主題分佈{ P(zi), i =1,2,3 } = {0.4,0.5,0.1}。

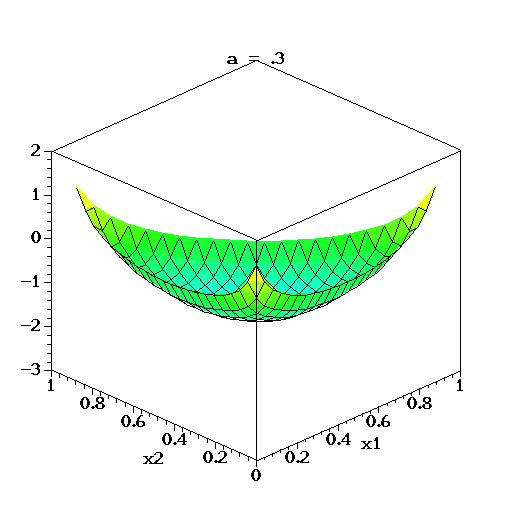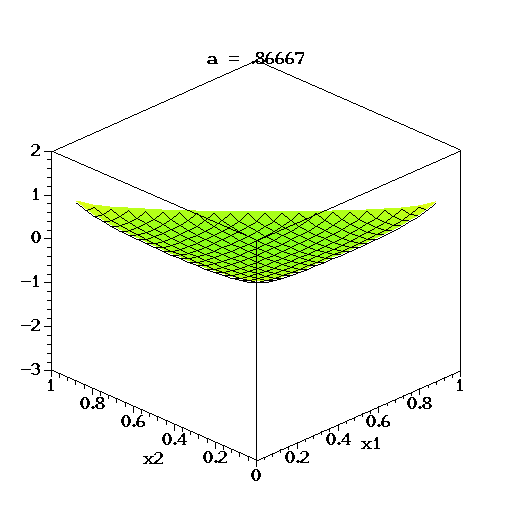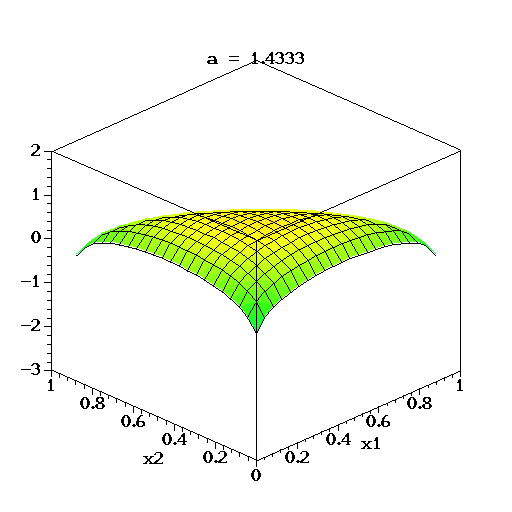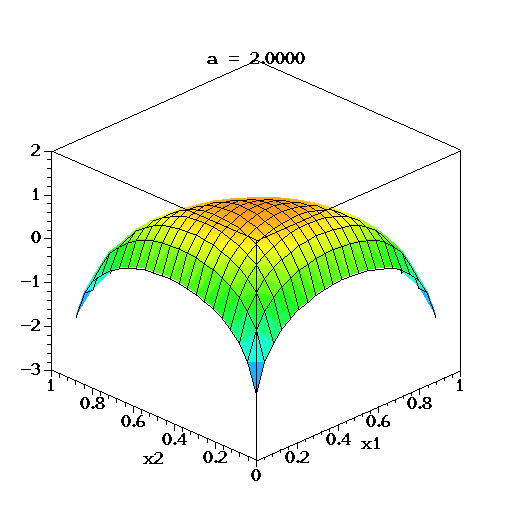
    可以想象到，空間裏有很多這樣的點(p1,p2,p3)，意味着有很多的主題分佈可供選擇，那dirichlet分佈如何選擇主題分佈呢？把上面的斜三角形放倒，映射到底面的平面上，便得到如下所示的一些彩圖（3個彩圖中，每一個點對應一個主題分佈，高度代表某個主題分佈被dirichlet分佈選中的概率，且選不同的

，dirichlet 分佈會偏向不同的主題分佈）：

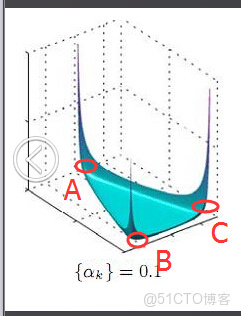
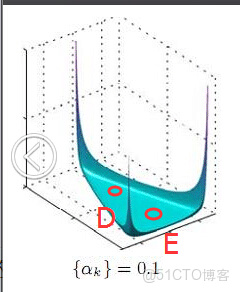
    我們來看上圖中左邊這個圖，高度就是代表dirichlet分佈選取某個座標點(p1,p2,p3)（這個點就是一個主題分佈）的概率大小。如下圖所示，平面投影三角形上的三個頂點上的點：A=(0.9,0.05,0.05)、B=(0.05,0.9,0.05)、C=(0.05,0.05,0.9)各自對應的主題分佈被dirichlet分佈選中的概率值很大，而平面三角形內部的兩個點：D、E對應的主題分佈被dirichlet分佈選中的概率值很小。

    所以雖然説dirichlet分佈是隨機選取任意一個主題分佈的，但依然存在着P(A) = P(B) = P(C) >> P(D) = P(E)，即dirichlet分佈還是“偏愛”某些主題分佈的。至於dirichlet分佈的參數

是如何決定dirichlet分佈的形狀的，可以從dirichlet分佈的定義和公式思考。

    此外，就算説“隨機”選主題也是根據主題分佈來“隨機”選取，這裏的隨機不是完全隨機的意思，而是根據各個主題出現的概率值大小來抽取。比如當dirichlet先驗為文檔d生成的主題分佈{ P(zi), i =1,2,3 }是{0.4,0.5,0.1}時，那麼主題z2在文檔d中出現的概率便是0.5。所以，從主題分佈中抽取主題，這個過程也不是完全隨機的，而是按照各個主題出現的概率值大小進行抽取。

4.3.3 pLSA跟LDA的概率圖對比

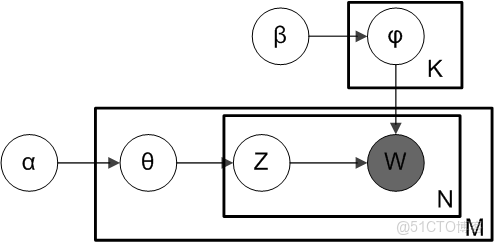
    接下來，對比下LDA跟pLSA的概率模型圖模型，左圖是pLSA，右圖是LDA（右圖不太規範，z跟w都得是小寫， 其中，陰影圓圈表示可觀測的變量，非陰影圓圈表示隱變量，箭頭表示兩變量間的條件依賴性conditional dependency，方框表示重複抽樣，方框右下角的數字代表重複抽樣的次數）：

    對應到上面右圖的LDA，只有W / w是觀察到的變量，其他都是隱變量或者參數，其中，Φ表示詞分佈，Θ表示主題分佈，

 是主題分佈Θ的先驗分佈（即Dirichlet 分佈）的參數，

是詞分佈Φ的先驗分佈（即Dirichlet 分佈）的參數，N表示文檔的單詞總數，M表示文檔的總數。

    所以，對於一篇文檔d中的每一個單詞，LDA根據先驗知識

確定某篇文檔的主題分佈θ，然後從該文檔所對應的多項分佈（主題分佈）θ中抽取一個主題z，接着根據先驗知識

確定當前主題的詞語分佈ϕ，然後從主題z所對應的多項分佈（詞分佈）ϕ中抽取一個單詞w。然後將這個過程重複N次，就產生了文檔d。

    換言之：

2. 假定語料庫中共有M篇文章，每篇文章下的Topic的主題分佈是一個從參數為



3. 的Dirichlet先驗分佈中採樣得到的Multinomial分佈，每個Topic下的詞分佈是一個從參數為



4. 的Dirichlet先驗分佈中採樣得到的Multinomial分佈。
5. 對於某篇文章中的第n個詞，首先從該文章中出現的每個主題的Multinomial分佈（主題分佈）中選擇或採樣一個主題，然後再在這個主題對應的詞的Multinomial分佈（詞分佈）中選擇或採樣一個詞。不斷重複這個隨機生成過程，直到M篇文章全部生成完成。

    綜上，M 篇文檔會對應於 M 個獨立的 Dirichlet-Multinomial 共軛結構，K 個 topic 會對應於 K 個獨立的 Dirichlet-Multinomial 共軛結構。

• 其中，



• →θ→z 表示生成文檔中的所有詞對應的主題，顯然 



• →θ 對應的是Dirichlet 分佈，θ→z 對應的是 Multinomial 分佈，所以整體是一個 Dirichlet-Multinomial 共軛結構，如下圖所示：

• 類似的，



• →φ→w，容易看出， 此時β→φ對應的是 Dirichlet 分佈， φ→w 對應的是 Multinomial 分佈， 所以整體也是一個Dirichlet-Multinomial 共軛結構，如下圖所示：

4.3.4 pLSA跟LDA參數估計方法的對比

    上面對比了pLSA跟LDA生成文檔的不同過程，下面，咱們反過來，假定文檔已經產生，反推其主題分佈。那麼，它們估計未知參數所採用的方法又有什麼不同呢？

• 在pLSA中，我們使用EM算法去估計“主題-詞項”矩陣Φ（由



• 轉換得到）和“文檔-主題”矩陣Θ（由



• 轉換得到）這兩個參數，而且這兩參數都是個固定的值，只是未知，使用的思想其實就是極大似然估計MLE。
• 而在LDA中，估計Φ、Θ這兩未知參數可以用變分(Variational inference)-EM算法，也可以用gibbs採樣，前者的思想是最大後驗估計MAP（MAP與MLE類似，都把未知參數當作固定的值），後者的思想是貝葉斯估計。貝葉斯估計是對MAP的擴展，但它與MAP有着本質的不同，即貝葉斯估計把待估計的參數看作是服從某種先驗分佈的隨機變量。
• 關於貝葉斯估計再舉個例子。假設中國的大學只有兩種：理工科和文科，這兩種學校數量的比例是1:1，其中，理工科男女比例7:1，文科男女比例1:7。某天你被外星人隨機扔到一個校園，問你該學校可能的男女比例是多少？然後，你實際到該校園裏逛了一圈，看到的5個人全是男的，這時候再次問你這個校園的男女比例是多少？

1. 因為剛開始時，有先驗知識，所以該學校的男女比例要麼是7:1，要麼是1:7，即P(比例為7:1) = 1/2，P(比例為1:7) = 1/2。
2. 然後看到5個男生後重新估計男女比例，其實就是求P(比例7:1|5個男生）= ？，P(比例1:7|5個男生) = ？
4. 用貝葉斯公式



5. ，可得：P(比例7:1|5個男生) = P(比例7:1)*P(5個男生|比例7:1) / P(5個男生)，P(5個男生)是5個男生的先驗概率，與學校無關，所以是個常數；類似的，P(比例1:7|5個男生) = P((比例1:7)*P(5個男生|比例1:7)/P(5個男生)。
6. 最後將上述兩個等式比一下，可得：P(比例7:1|5個男生)/P(比例1:7|5個男生) = {P((比例7:1)*P(5個男生|比例7:1)} / { P(比例1:7)*P(5個男生|比例1:7)}。

    由於LDA把要估計的主題分佈和詞分佈看作是其先驗分佈是Dirichlet分佈的隨機變量，所以，在LDA這個估計主題分佈、詞分佈的過程中，它們的先驗分佈（即Dirichlet分佈）事先由人為給定，那麼LDA就是要去求它們的後驗分佈（LDA中可用gibbs採樣去求解它們的後驗分佈，得到期望

、

）！

   此外，不厭其煩的再插一句，在LDA中，主題分佈和詞分佈本身都是多項分佈，而由上文3.2節可知“Dirichlet分佈是多項式分佈的共軛先驗概率分佈”，因此選擇Dirichlet 分佈作為它們的共軛先驗分佈。意味着為多項分佈的參數p選取的先驗分佈是Dirichlet分佈，那麼以p為參數的多項分佈用貝葉斯估計得到的後驗分佈仍然是Dirichlet分佈。

4.3.5 LDA參數估計：Gibbs採樣

    理清了LDA中的物理過程，下面咱們來看下如何學習估計。

    類似於pLSA，LDA的原始論文中是用的變分-EM算法估計未知參數，後來發現另一種估計LDA未知參數的方法更好，這種方法就是：Gibbs Sampling，有時叫Gibbs採樣或Gibbs抽樣，都一個意思。Gibbs抽樣是馬爾可夫鏈蒙特卡爾理論（MCMC）中用來獲取一系列近似等於指定多維概率分佈（比如2個或者多個隨機變量的聯合概率分佈）觀察樣本的算法。

    OK，給定一個文檔集合，w是可以觀察到的已知變量，

和

是根據經驗給定的先驗參數，其他的變量z，θ和φ都是未知的隱含變量，需要根據觀察到的變量來學習估計的。根據LDA的圖模型，可以寫出所有變量的聯合分佈：

    注：上述公式中及下文中，

等價上文中定義的

，

等價於上文中定義的

，

等價於上文中定義的

，等價於上文中定義的

。

    因為

產生主題分佈θ，主題分佈θ確定具體主題，且

產生詞分佈φ、詞分佈φ確定具體詞，所以上述式子等價於下述式子所表達的聯合概率分佈

：

    其中，第一項因子

表示的是根據確定的主題

和詞分佈的先驗分佈參數

採樣詞的過程，第二項因子

是根據主題分佈的先驗分佈參數

採樣主題的過程，這兩項因子是需要計算的兩個未知參數。

    由於這兩個過程是獨立的，所以下面可以分別處理，各個擊破。

    第一個因子

，可以根據確定的主題

和從先驗分佈

取樣得到的詞分佈Φ產生：

    由於樣本中的詞服從參數為主題

的獨立多項分佈，這意味着可以把上面對詞的乘積分解成分別對主題和對詞的兩層乘積：

    其中，

是詞 t 在主題 k 中出現的次數。

    回到第一個因子上來。目標分佈

需要對詞分佈Φ積分，且結合我們之前在3.1節定義的Dirichlet 分佈的歸一化係數

的公式

    可得：

    這個結果可以看作K個Dirichlet-Multinomial模型的乘積。

    現在開始求第二個因子

。類似於

的步驟，先寫出條件分佈，然後分解成兩部分的乘積：

    其中，

 表示的單詞 i 所屬的文檔，

是主題 k 在文章 m 中出現的次數。

    對主題分佈Θ積分可得：

    綜合第一個因子和第二個因子的結果，得到

的聯合分佈結果為：

    接下來，有了聯合分佈

，咱們便可以通過聯合分佈來計算在給定可觀測變量 w 下的隱變量 z 的條件分佈（後驗分佈）

來進行貝葉斯分析。

    換言之，有了這個聯合分佈後，要求解第m篇文檔中的第n個詞（下標為

的詞）的全部條件概率就好求了。

    先定義幾個變量。

表示除去

的詞，

，

。

    然後，排除當前詞的主題分配，即根據其他詞的主題分配和觀察到的單詞來計算當前詞主題的概率公式為：

    勘誤：考慮到

，所以上述公式的第二行的分子，非p(w,z) *p(z)，而是p(w|z)*p(z)。

    且有：

    最後一步，便是根據Markov鏈的狀態

獲取主題分佈的參數Θ和詞分佈的參數Φ。

    換言之根據貝葉斯法則和Dirichlet先驗，以及上文中得到的

和

各自被分解成兩部分乘積的結果，可以計算得到每個文檔上Topic的後驗分佈和每個Topic下的詞的後驗分佈分別如下（據上文可知：其後驗分佈跟它們的先驗分佈一樣，也都是Dirichlet 分佈）：

    其中，

是構成文檔m的主題數向量，

是構成主題k的詞項數向量。

    此外，別忘了上文中2.4節所述的Dirichlet的一個性質，如下：

     “ 如果

，同樣可以證明有下述結論成立：

    即：如果

，則

中的任一元素

的期望是：

    可以看出，超參數

的直觀意義就是事件先驗的偽計數(prior pseudo-count)。 ”

    所以，最終求解的Dirichlet 分佈期望為：

    然後將

和

的結果代入之前得到的

的結果中，可得：

    仔細觀察上述結果，可以發現，式子的右半部分便是

，這個概率的值對應着

的路徑概率。如此，K 個topic 對應着K條路徑，Gibbs Sampling 便在這K 條路徑中進行採樣，如下圖所示：

    何等奇妙，就這樣，Gibbs Sampling通過求解出主題分佈和詞分佈的後驗分佈，從而成功解決主題分佈和詞分佈這兩參數未知的問題。