前言:
希爾排序(Shell Sort)是一種基於插入排序的排序算法,它的核心思想是通過將待排序元素按一定間隔分成若干組,並對每個組進行插入排序,進而達到加速排序的目的。
希爾排序開創性地突破了O(N²)時間複雜度瓶頸,成為計算機科學史上首個實現這一突破的排序算法。相較於傳統的插入、選擇和冒泡排序,它在性能上實現了質的飛躍。
一、傳統插入排序的缺陷
為了更好地理解希爾排序的優勢,我們首先回顧一下傳統插入排序的工作原理。
插入排序的核心思想是將一個元素插入到已經排好序的部分,逐步構建整個排序。它的時間複雜度為O(N²) ,這是因為每插入一個元素,都需要和之前的元素逐一比較,最壞情況下每次插入都要進行n次比較和交換。
例如:假設我們需要對一個逆序數組[6,5,4,3,2,1]進行升序排序。在這種情況下,每個待插入元素都需要與已排序部分逐個比較和交換,導致性能下降,這是因為插入操作只能逐步向前移動。
那麼,是否可以通過"跳式"多步的方式比較來優化插入排序呢? 希爾排序由此應運而生。
二、希爾排序的工作原理
希爾排序通過引入增量(gap)優化了插入排序,它通過逐步減小間隔(gap),將待排序數組劃分成多個小的子序列,每個子序列通過插入排序來進行排序。
由於插入排序本身對已經部分有序的數組較為高效,希爾排序通過逐步縮小間隔,使得整個數組在多輪排序中逐步趨向有序,最終gap減小至1,執行插入排序使得整個數組有序。
其核心步驟如下所示:
①設定初始增量gap值,將數組元素按gap間隔分組
②對每個分組執行插入排序
③逐步減小gap值,重複分組排序過程
④當gap減至1時,執行標準插入排序完成最終排序
其中每次排序讓數組接近有序的過程叫做預排序,最後一次排序是插入排序
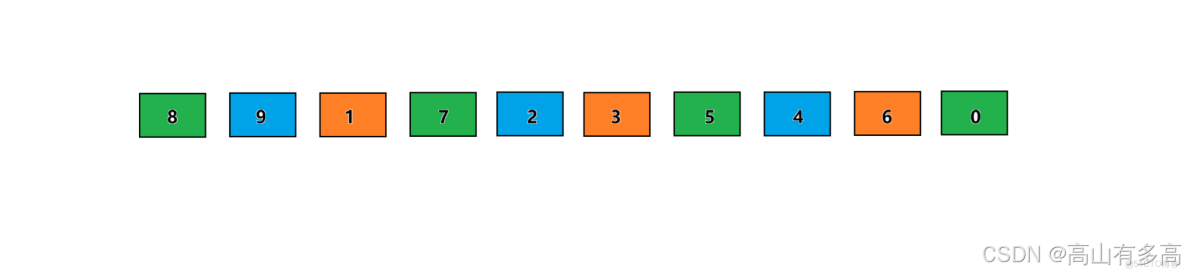
以待排序數組 [8,9,1,7,2,3,5,4,6,0] 為例講解希爾排序分組過程
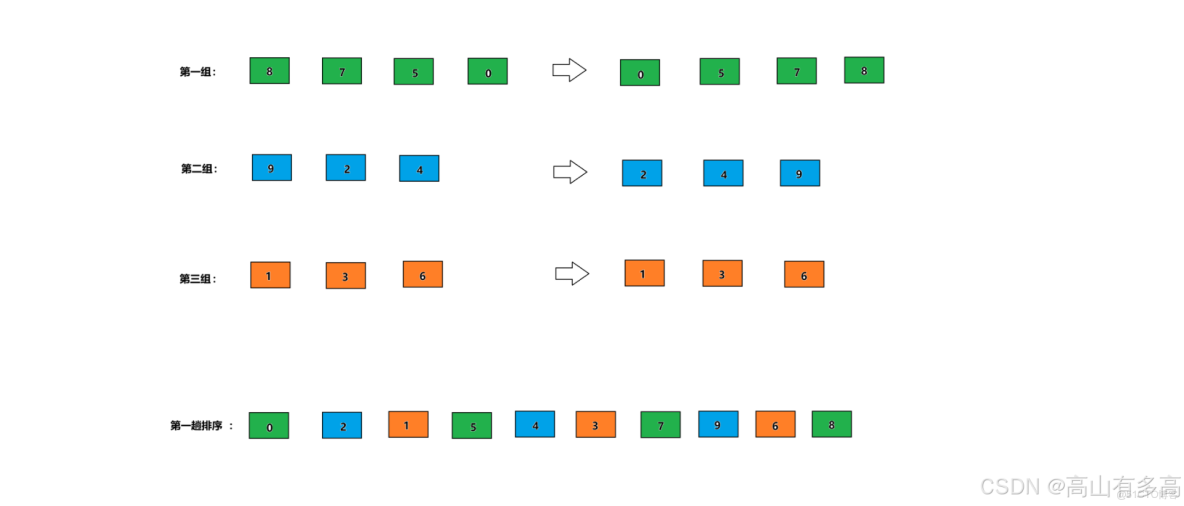
1.以gap=3為增量,進行如下分組,如下所示待排序數組被分為三組
2.對每一組進行插入排序,則可得到如下數組
3.此時gap增量縮小,以gap=2為增量對數組進行分組,數組將被分成2份,每組之間都是2的等差數列
4.最後gap為1,以gap=1進行分組,相當於沒有進行分組,就相當於進行插入排序
三、希爾排序的改進之處
對比第一次排序前後的結果可以發現,原本位於數組頭部數值的較大元素,經過分組排序後迅速被移動到了數組尾部。
這種排序方式採用增量步長來騰出插入位置,相比普通插入排序一次移動一步的方式效率顯著提升。
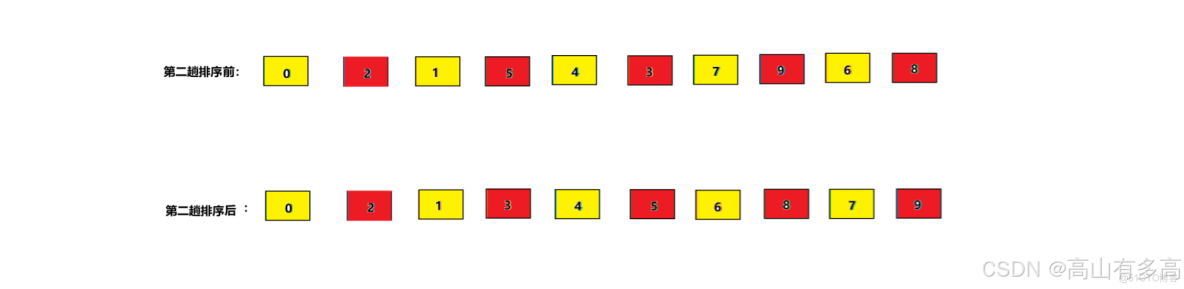
第一次排序後,我們採用更小的增量進行分組,經過第二趟排序以後,組與組之間更加有序
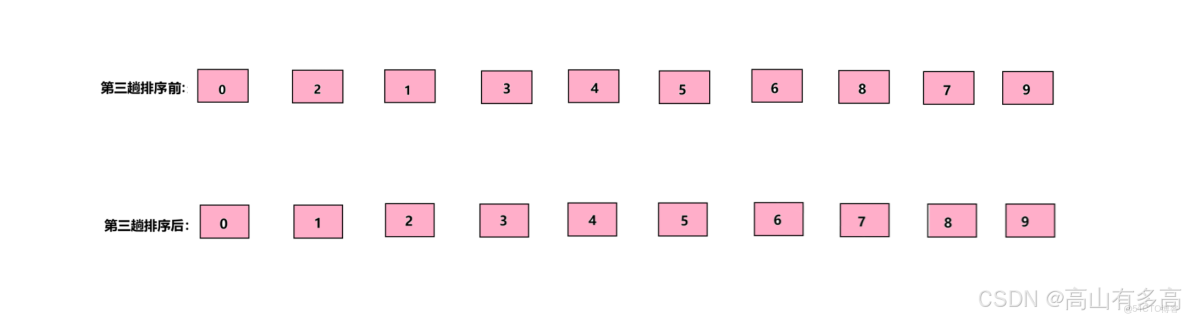
經過第二次排序後,我們採用gap=1的分組方式進行排序,這實際上等同於直接插入排序。
值得注意的是,此時的數組已接近有序狀態。最初的無序數組直接執行插入排序操作與預排序之後再進行直接插入排序,所需的比較和移動次數將明顯增多。
由上述,我們可以發現:
①當 gap 值越大時,數據會被分成更多組,組與組之間的有序程度越低;
②當 gap 值越小時,分組數量越少,組與組之間的有序程度越高;當 gap=1 時,該排序方式等價於插入排序。
③同時gap的值決定了分組的個數,因為每gap距離分為一組,所以gap的值為多少,待排數列就可以分為多少組。
例如:待排數列為 [8,9,1,7,2,3,5,4,6,0]
當
gap = 3時:
我們將數組按間隔
3分成多個組:
①組1:索引為 0, 3, 6, 9 的元素。
②組2:索引為 1, 4, 7 的元素。
③組3:索引為 2, 5, 8 的元素
四、希爾排序的分組策略
希爾排序中gap的選取沒有 “絕對最優” 的統一規則,但有幾種經典且常用的序列方案
核心原則是:初始 gap 要足夠大以快速減少逆序對,後續逐步縮小,最終必須降到 1(保證數組完全有序)。
①希爾祖師爺提出的增量是
gap = n / 2
②Knuth大佬提出的gap = [gap / 3] + 1
五、希爾排序的代碼實現
對於希爾排序代碼實現的過程十分抽象難懂,由於我們講解的希爾排序的思路是將待排序數組進行分組後,進行直接插入排序,這也就導致我們容易產生疑惑,是不是分多少組就調用多少次插入排序的代碼呢?
實則不然,我們可以通過用一次遍歷數組的方式,巧妙地對每個分組完成單趟排序,不需要對代碼進行很複雜抽象的操作。
我們依然可以採用先局部再整體的方式進行對數組的排序: 假設gap的初始值為3,初始時對待排序數組進行分三組
[8,9,1,7,2,3,5,4,6,0] 為例進行代碼的講解
核心思路:對於第一組(綠色方塊)的元素而言:進行插入排序的思路,通過將待排序的數組[ 7 , 5 , 0 ] ,插入到已經有序的數組 [ 8 ] 。
①定義變量end表示:有序數組中的最後一個元素下標
②定義tmp表示:待排序數組中,當前要插入到有序數組中的元素值,即tmp=a[end+gap]
例如:初始時已經有序的數組為[8],需要將a[end+gap]的值 7 插入到已經有序的數組中
③遍歷第一組(綠色方塊)的元素而言,每遍歷一個元素需要跨越gap步的距離,而不是固定思維跨越一步的距離
④確定end的範圍:為了使得待排序數組中的最後一個元素a[end+gap]也能插入到有序數組中,則end的最大值只能為n-gap-1,
故而確定得到end<gap-n
5.1、排序一組
由上述思路我們可以對綠色這一組進行排序
//數組:[8,9,1,7,2,3,5,4,6,0]
//下標:[0,1,2,3,4,5,6,7,8,9]
//進行升序排序
//假設gap=3
int gap = 3;
for (int i = 0; i < n - gap; i += gap)
{
//end下標為有序數組中的最後一個元素下標
int end = i;
//當前需要進行插入的元素
int tmp = a[end + gap];
//進行插入
while (end >= 0)
{
if (tmp < a[end])
{
//a[end]往後移動
a[end + gap] = a[end];
//向前跨越gap進行遍歷
end -= gap;
}
else
{
//找到合適的位置
break;
}
}
//退出while循環有兩種情況
//情況一:當前插入的元素,在向前比較時,已排序數組中沒有比其更小的,因不滿足end>=0而退出
//情況二:當前插入的元素,在向前比較的時候找到了合適的位置,因break而退出
a[end + gap] = tmp;
}通過該段代碼,此時數組預期結果為:[0 9 1 5 2 3 7 4 6 8]
5.2、排序多組
有了排序綠色方塊一組的基礎,如果想要排序其他組,只需要在此基礎上再添加一層循環,控制每組的起始位置就能夠排序其餘其他的組次
//數組:[8,9,1,7,2,3,5,4,6,0]
//下標:[0,1,2,3,4,5,6,7,8,9]
//進行升序排序
//假設gap=3
int gap = 3;
//控制每組的起始位置
for (int k = 0; k < gap; k++)
{
for (int i = k; i < n - gap; i += gap)
{
//end下標為有序數組中的最後一個元素下標
int end = i;
//當前需要進行插入的元素
int tmp = a[end + gap];
//進行插入
while (end >= 0)
{
if (tmp < a[end])
{
//a[end]往後移動
a[end + gap] = a[end];
//向前跨越gap進行遍歷
end -= gap;
}
else
{
//找到合適的位置
break;
}
}
//退出while循環有兩種情況
//情況一:當前插入的元素,在向前比較時,已排序數組中沒有比其更小的,因不滿足end>=0而退出
//情況二:當前插入的元素,在向前比較的時候找到了合適的位置,因break而退出
a[end + gap] = tmp;
}
}
通過該段代碼,此時數組預期結果為:[0 2 1 5 4 3 7 9 6 8]
5.3、縮小gap
我們通過縮小gap值的方式,數組從預排序變為幾乎完全有序狀態,最後當gap=1時,數組變為有序
//以數組:[8,9,1,7,2,3,5,4,6,0]
// 下標:[0,1,2,3,4,5,6,7,8,9]
//進行升序排序
//假設gap=3
int gap = 3;
//由於採用的是gap--的方式縮小gap,所以gap=1時也要進入
while (gap >= 1)
{
for (int k = 0; k < gap; k++)
{
for (int i = k; i < n - gap; i += gap)
{
//end下標為有序數組中的最後一個元素下標
int end = i;
//當前需要進行插入的元素
int tmp = a[end + gap];
//進行插入
while (end >= 0)
{
if (tmp < a[end])
{
//a[end]往後移動
a[end + gap] = a[end];
//向前跨越gap進行遍歷
end -= gap;
}
else
{
//找到合適的位置
break;
}
}
//退出while循環有兩種情況
//情況一:當前插入的元素,在向前比較時,已排序數組中沒有比其更小的,因不滿足end>=0而退出
//情況二:當前插入的元素,在向前比較的時候找到了合適的位置,因break而退出
a[end + gap] = tmp;
}
gap--;
}
}
通過該段代碼後,此時數組預期結果為:[0 1 2 3 4 5 6 7 8 9]
思考如下問題:
1.這僅僅是在gap=3的基礎上實現,但每次分組只能為3嗎?
2.每次縮小增量gap只能每次減小1嗎?
答:當然不是,我們一般採用,Knuth大佬提出的gap = [gap / 3] + 1 或則 希爾祖師爺提出的增量 gap = n / 2 進行分組實現預排序
用上述增量的方式也能使得最後一次排序時gap=1,轉變為直接插入排序。
5.4、完整實現
於是我們可以進行更改上述代碼,採用這兩種增量的方式調整gap,從而得到最終版本的希爾排序:
//以數組:[8,9,1,7,2,3,5,4,6,0]
// 下標:[0,1,2,3,4,5,6,7,8,9]
//進行升序排序
//假設gap=3
int gap = n;
while (gap > 1)
{
//shell增量 gap=gap/2
//knuth增量 gap=gap/3+1
gap = gap / 3 + 1;
for (int k = 0; k < gap; k++)
{
for (int i = k; i < n - gap; i += gap)
{
//end下標為有序數組中的最後一個元素下標
int end = i;
//當前需要進行插入的元素
int tmp = a[end + gap];
//進行插入
while (end >= 0)
{
if (tmp < a[end])
{
//a[end]往後移動
a[end + gap] = a[end];
//向前跨越gap進行遍歷
end -= gap;
}
else
{
//找到合適的位置
break;
}
}
//退出while循環有兩種情況
//情況一:當前插入的元素,在向前比較時,已排序數組中沒有比其更小的,因不滿足end>=0而退出
//情況二:當前插入的元素,在向前比較的時候找到了合適的位置,因break而退出
a[end + gap] = tmp;
}
}
}
代碼疑難點剖析:
int gap = n; while (gap > 1) { gap = gap / 3 + 1; //... }
想必對於這一部分邏輯會很疑惑,為什麼這樣控制gap呢?
之所以這樣寫,主要有兩個原因:保證最後一次gap的值一定是 1,以及防止死循環。
1.while循環的條件
gap > 1: 保證了只要 gap 還沒變到 1,就繼續縮小,而且它把 gap = 2 放進來作為最後一次循環的臨界條件,當gap=2時,配合gap的調整表達式使得gap=1,保證了最後一次循環進行的是插入排序。
2.gap處理的表達式
gap=gap / 3 + 1 : 每次 gap = gap / 3 + 1 計算,實際上是通過不斷除以3和加1的方式逐漸減小gap的值,直到最後gap為1,加1有效的避免了因為整數除法被截斷導致gap=0,而造成了死循環導致程序卡死。
這兩段代碼十分巧妙的結合在一起,感嘆一下大佬們的智商
實例推演 (Trace) 🔍
讓我們用一個具體的數字
gap = 8來跑一遍這個邏輯:
初始狀態:gap = 8
第 1 次判斷:8 > 1?👉 Yes。進入循環。
更新 gap:gap = 8 / 3 + 1 = 2 + 1 = 3。
執行排序:以 3 為增量進行排序。
第 2 次判斷:3 > 1?👉 Yes。繼續循環。
更新 gap:gap = 3 / 3 + 1 = 1 + 1 = 2。
執行排序:以 2 為增量進行排序。
第 3 次判斷:2 > 1?👉 Yes。繼續循環。
更新 gap:gap = 2 / 3 + 1 = 0 + 1 = 1。
執行排序:以 1 為增量進行排序。(注意:這裏完成了最終的插入排序)
第 4 次判斷:1 > 1?👉 No。
退出循環,排序結束。
六、希爾排序代碼的總結
6.1寫法一(方便理解的寫法)
通過gap進行分組後,一組一組排序
void ShellSort(int* a, int n)
{
//以數組:[8,9,1,7,2,3,5,4,6,0]
// 下標:[0,1,2,3,4,5,6,7,8,9]
//進行升序排序
//假設gap=3
int gap = n;
while (gap > 1)
{
//shell增量 gap=gap/2
//knuth增量 gap=gap/3+1
gap = gap / 3 + 1;
for (int k = 0; k < gap; k++)
{
for (int i = k; i < n - gap; i += gap)
{
//end下標為有序數組中的最後一個元素下標
int end = i;
//當前需要進行插入的元素
int tmp = a[end + gap];
//進行插入
while (end >= 0)
{
if (tmp < a[end])
{
//a[end]往後移動
a[end + gap] = a[end];
//向前跨越gap進行遍歷
end -= gap;
}
else
{
//找到合適的位置
break;
}
}
//退出while循環有兩種情況
//情況一:當前插入的元素,在向前比較時,已排序數組中沒有比其更小的,因不滿足end>=0而退出
//情況二:當前插入的元素,在向前比較的時候找到了合適的位置,因break而退出
a[end + gap] = tmp;
}
}
}
}
6.2寫法二(主流書上的寫法)
通過gap進行分組後,組與組之間交替的進行排序
這是在寫法一的基礎上進行改進減少代碼量,但是在性能上與寫法一沒有本質區別,只是邏輯發生了改變,寫法一是一組一組排,當一組排序完畢後,另一組才開始繼續排需要多一層循環控制組數的起點
以下圖為例,對於寫法二而言,這是組與組之間交替着排序,當綠色一組排序完一個,輪替到藍色一組排序一個,再輪替到橙色一組排序一個,這也交替着進行,多組並行的方式進行調整各自組的有序性。
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
//預排序
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
七、希爾排序複雜度分析
時間複雜度分析
對於希爾排序的時間複雜度沒有明確的數學表達式進行定量分析,但是經過大量數據驗證認定:
|
增量序列類型 |
最壞時間複雜度 |
平均時間複雜度 |
適用場景 |
|
二分增量(傳統) |
O(n²) |
O(n²) |
教學演示,無需追求效率的場景 |
|
Hibbard 序列 |
O(n^(1.5)) |
O(n^(1.3)) |
平衡效率與實現複雜度,推薦首選 |
|
Sedgewick 序列 |
O(n log²n) |
接近 O (n log n) |
大規模數據,追求極致效率 |
空間複雜度分析
希爾排序的空間複雜度為 O(1),屬於 “原地排序” 算法。