前言：

我菜菜菜菜菜菜，所以只改了兩道題。

noip模擬題7 - Geek_i++

T2：原子（atom）

思路：

建圖圖圖圖圖。

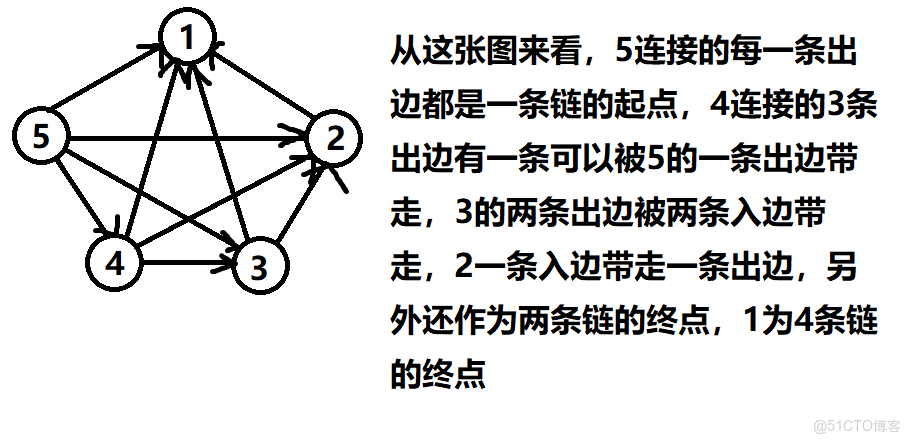
根據題意我們可以建出來一個完全圖，然後求出圖中最少有幾條鏈就行。

我們發現，鏈的數量其實就是每個點的（出度減去入度）的加和。

然後再所有的把鏈跑出來就行。

提一嘴，隊列是簡單的，但是鏈式前向星是可寫的。

noip模擬題7 - Geek_子節點_02

代碼：

$code$ 

#include<iostream>
#include<queue>
using namespace std;
const int N=2005;
int n,ans,du[N];
queue<int> e[N],q;
int main(){
	freopen("atom.in","r",stdin);
	freopen("atom.out","w",stdout);
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<n;i++){
		for(int j=i+1;j<=n;j++){
			e[i].push(j);
			du[i]++;du[j]--;
		}
	}
	for(int i=1;i<=n;i++) if(du[i]>0) ans+=du[i];
	cout<<ans<<'\n';
	int i=1;
	while(1){
		while(e[i].empty()&&i<=n) i++;
		if(i>n) break;
		int x=i,cnt=0;
		if(x>1){
			q.push(x-1);
			cnt++;
		}
		while(!e[x].empty()){
			cnt++;
			int y=e[x].front();e[x].pop();
			q.push(y-x);
			x=y;
		}
		cout<<cnt<<' ';
		while(!q.empty()){
			cout<<q.front()<<' ';
			q.pop();
		}
		cout<<'\n';
	}
	return 0;
}

T3：旅行計劃（plan）

思路：

竟然是 \(3\) 個 \(dp\)

對於每一個點的狀態，可以分為三種情況：出去一次，出去又回來，出去兩趟。分別對它們進行狀態轉移。

先説出去又回來的。那先顯然是它的子節點出去又回來的長度加和再加上這個點到子節點的重複路徑數/2*2。

再説出去兩趟的。顯然是要求出出去一趟的最大值和次大值然後加和再加上從這個點出去又回來的路徑長度，在和它的子節點的出去兩趟的 \(dp\) 值加上該點到子節點的重複路徑數/2*2取一下 \(max\)

最後是出去一次的。就是這個點的所有子節點出去一次的最大值加上改點到子節點的(最長路徑數 \(-1)/2*2\)，再加上出去又回來的路徑長度。

代碼：

$code$ 

#include<iostream>
#include<cstring>
#define int long long
using namespace std;
const int N=1e6+5;
int T,n,u,v,w,d1,d2,d3,cnt,head[N],f1[N],f2[N],f3[N];
struct flower{
	int to,nxt,val;
}e[N<<1];
inline void add(int x,int y,int z){
	e[++cnt].to=y;
	e[cnt].val=z;
	e[cnt].nxt=head[x];
	head[x]=cnt;
}
inline void dfs(int x,int fa){
	f1[x]=f2[x]=f3[x]=0;
	int maxn=0,maxx=0;
	for(int i=head[x];i;i=e[i].nxt){
		int y=e[i].to,z=e[i].val;
		if(y==fa) continue;
		dfs(y,x);
		if(z/2>=1){
			d3=z/2*2+f3[y];
			d2=z/2*2+f2[y]-d3;
		}else d2=d3=0;
		f2[x]=max(d2,f2[x]);
		f3[x]+=d3;
		d1=(z-1)/2*2+1+f1[y]-d3;
		if(d1>maxn){
			maxx=maxn;
			maxn=d1;
		}else if(d1>maxx) maxx=d1;
	}
	f1[x]=maxn+f3[x];
	f2[x]=max(f2[x],maxn+maxx)+f3[x];
}
signed main(){
	freopen("plan.in","r",stdin);
	freopen("plan.out","w",stdout);
	ios::sync_with_stdio(false);
	cin>>T;
	while(T--){
		cnt=0;
		memset(head,0,sizeof(head));
		cin>>n;
		for(int i=1;i<n;i++){
			cin>>u>>v>>w;
			add(u,v,w);add(v,u,w);
		}
		dfs(1,0);
		int ans=0;
		for(int i=1;i<=n;i++) ans=max(ans,max(f1[i],max(f2[i],f3[i])));
		cout<<ans<<'\n';
	}
	return 0;
}