一、差分算法簡介
1.1 簡介
差分算法的核心在於構建差分數組或矩陣,將對原始數據的複雜區間操作轉化為對差分數組特定端點值的簡單操作 ,從而實現對原數組的高效區間修改。在面對頻繁對數組某個區間的元素進行增減操作時,傳統方法往往需要對區間內每個元素逐一處理,時間複雜度較高;而差分算法通過巧妙的轉換,將這類操作的時間複雜度降至 O (1),大大提升了處理效率。
差分適用於頻繁對原始數組的某個區間的元素進行增減
二、差分算法基礎理論
2.1 一維差分
2.1.1 差分數組的概念
對於一個給定的一維數組 arr(長度為 length),其差分數組 diff 定義如下:diff[0] = arr[0],對於 i > 0,diff[i] = arr[i] - arr[i - 1]。差分數組記錄了原始數組中相鄰元素之間的差異。例如,原始數組 arr = [1, 3, 5, 7, 9],其差分數組 diff = [1, 2, 2, 2, 2]。
2.1.2 性質與原理
差分數組的核心性質:差分數組的前綴和即為原始數組。即對於任意的 i,有 arr[i] = diff[0] + diff[1] + ... + diff[i]。
當需要對原始數組的區間 [l, r](0-based)進行 +k 操作時,僅需修改差分數組的兩個端點:diff[l] += k、diff[r + 1] -= k。
避免邊界判斷的關鍵:一維場景中,若 r + 1 超出原始數組長度(即 r = length - 1),diff[r + 1] 的修改會作用於數組外的 “虛擬位置”,但由於後續計算前綴和時僅遍歷到 length - 1,該修改不會影響結果,因此無需額外判斷 r + 1 < length。
2.1.3 做題步驟與代碼實現
以 “區間加法” 問題為例:給定初始長度為 length 的全 0 數組,和一系列更新操作 updates(updates[i] = [startIdx, endIdx, inc]),返回執行完所有操作後的數組。
核心操作
diff[left] += val;
diff[right + 1] -= val;定義差分數組:直接初始化長度為 length + 1 的差分數組(額外的 1 個位置用於容納 r + 1 超出邊界的情況),無需判斷邊界
差分數組前綴和即為結果數組
int[] result = new int[length];
result[0] = diff[0];
for (int i = 1; i < length; i++) {
result[i] = result[i - 1] + diff[i];
}模板代碼演示
public int[] getModifiedArray(int length, int[][] updates) {
// 差分數組長度設為 length + 1,避免邊界判斷
int[] diff = new int[length + 1];
// 步驟 2:處理所有區間更新(無需判斷 endIdx + 1 是否越界)
for (int[] update : updates) {
int start = update[0];
int end = update[1];
int val = update[2];
diff[start] += val;
diff[end + 1] -= val; // 即使 end+1 = length,也不會越界
}
// 步驟 3:計算前綴和,還原結果數組
int[] result = new int[length];
result[0] = diff[0];
for (int i = 1; i < length; i++) {
result[i] = result[i - 1] + diff[i];
}
return result;
}2.2 二維差分
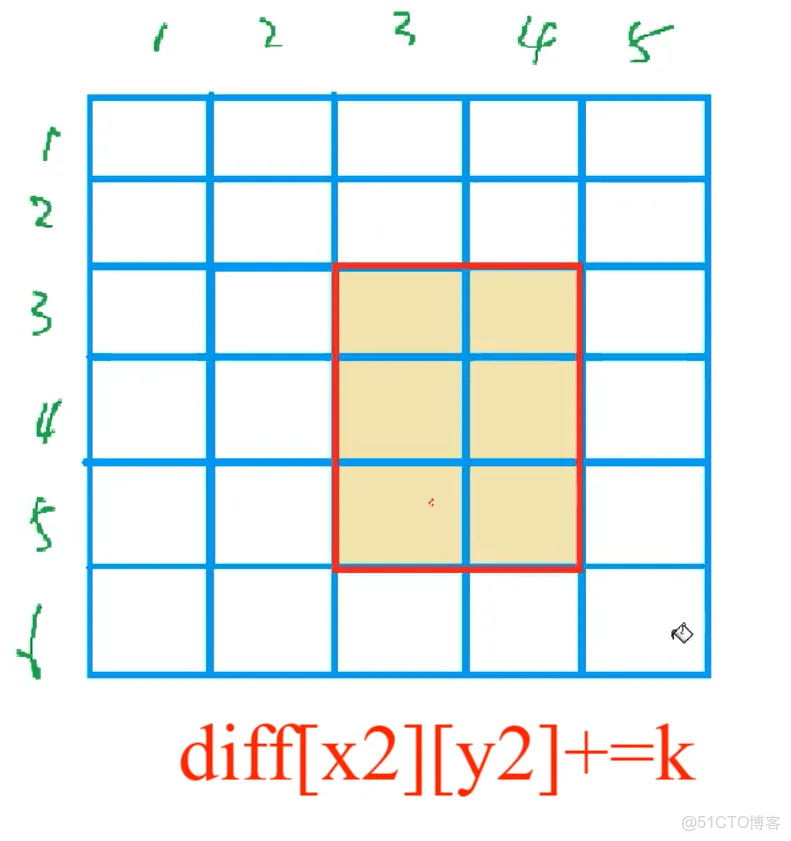
2.2.1 核心操作及邏輯
避免邊界判斷的關鍵:將差分矩陣的尺寸設為 (m + 2) × (n + 2)(比原始矩陣多 1 行 1 列),即使 x2 + 1 = m + 1 或 y2 + 1 = n + 1,修改也不會越界,且後續計算前綴和時僅遍歷原始矩陣的 m × n 範圍,多餘位置的修改不影響結果。
2.2.2 初始化差分矩陣
二維差分的初始化本質是:將原始矩陣的每個元素 matrix[i][j](1-based)視為 1×1 的矩形區域,執行 +matrix[i][j] 操作。利用 (m + 2) × (n + 2) 的差分矩陣,無需判斷 i+1 或 j+1 是否越界。
初始化代碼實現
// 初始化: 對 (i,j)~(i,j) 執行 +val 操作
diff[i][j] += val;
diff[i][j + 1] -= val;
diff[i + 1][j] -= val;
diff[i + 1][j + 1] += val;2.2.3 子矩陣更新與恢復原矩陣
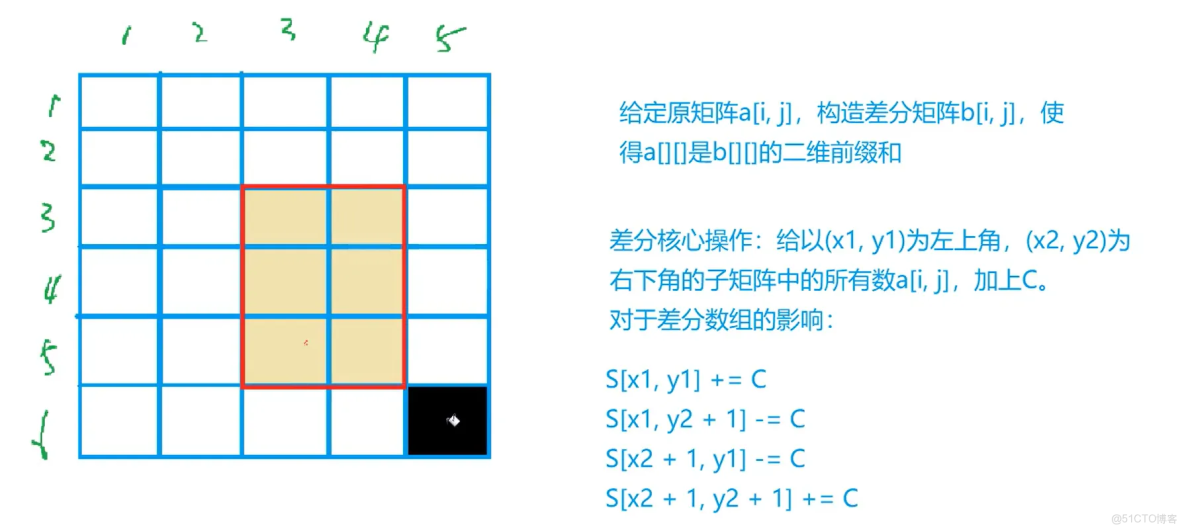
子矩陣更新:這是最核心的步驟
// 對矩形區域 (x1,y1)~(x2,y2) 執行 +val 操作
public void updateDiffMatrix(int[][] diff, int x1, int y1, int x2, int y2, int val) {
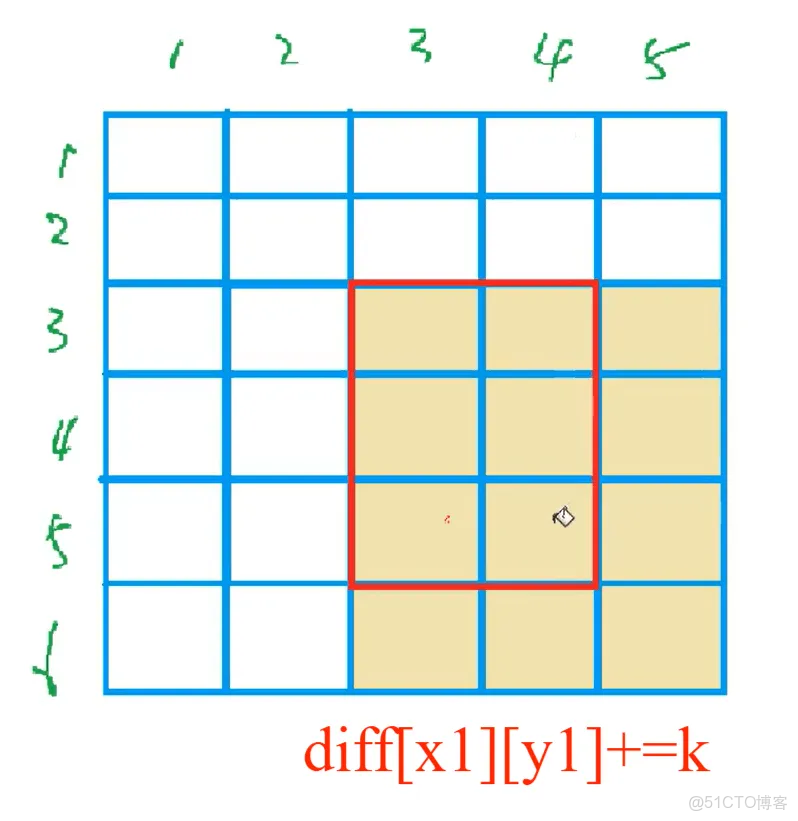
diff[x1][y1] += val;
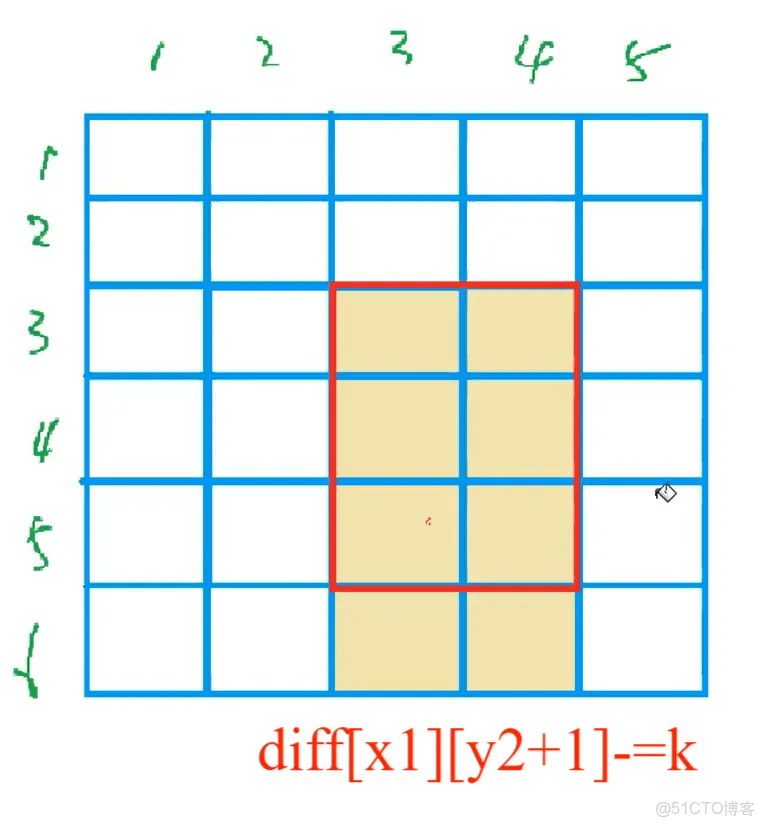
diff[x1][y2 + 1] -= val;
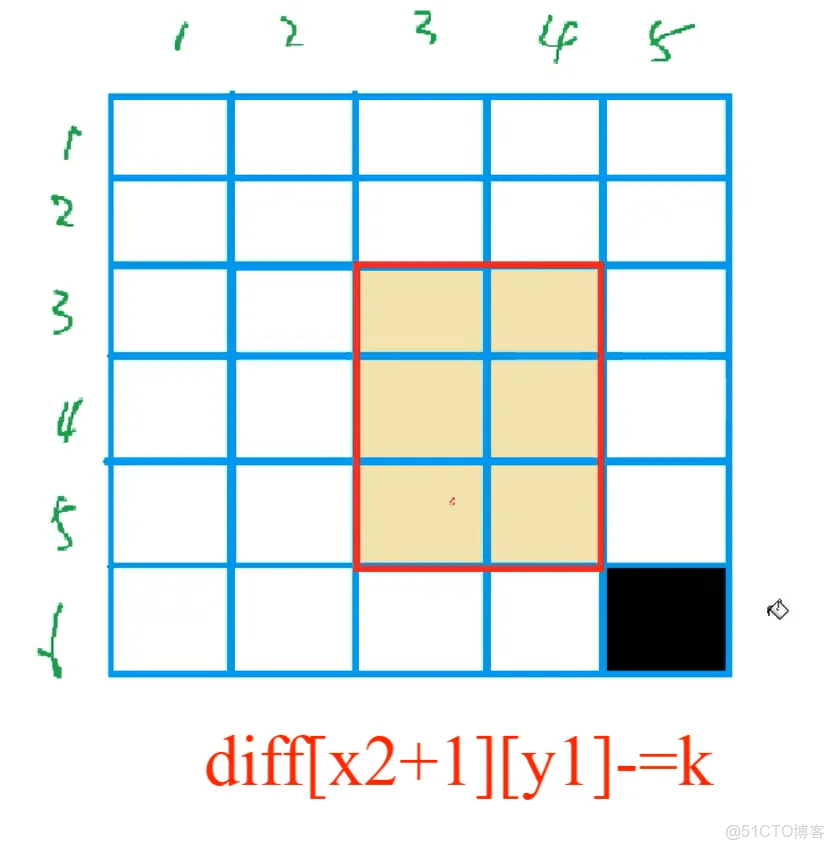
diff[x2 + 1][y1] -= val;
diff[x2 + 1][y2 + 1] += val; // 無需判斷 x2+1、y2+1 是否越界
}恢復原矩陣:二維前綴和即為結果數組
// 根據差分矩陣恢復 m 行 n 列的原始矩陣(1-based)
public int[][] recoverOriginalMatrix(int[][] diff, int m, int n) {
int[][] matrix = new int[m + 1][n + 1]; // 1-based 存儲結果
// 計算二維前綴和(先按行,再按列)
for (int i = 1; i <= m; i++) {
int rowSum = 0;
for (int j = 1; j <= n; j++) {
rowSum += diff[i][j];
matrix[i][j] = matrix[i - 1][j] + rowSum;
}
}
return matrix;
}三、差分算法適用場景
3.1 一維差分適用場景
批量數據區間調整
例如電商平台的 “限時折扣”:某商品的每日價格存儲在數組中,需對 [活動開始日, 活動結束日] 的價格統一減去折扣金額。使用一維差分(差分數組長度設為 n + 1),無需判斷邊界,直接修改區間端點即可。
統計區間覆蓋次數
例如地鐵客流量統計:給定每個乘客的乘車時間段 [進站時間, 出站時間],統計每個時間點的在站人數。通過差分將 “時間段覆蓋” 轉化為 diff[進站] += 1、diff[出站 + 1] -= 1,無需判斷邊界,最終前綴和即為每個時間點的人數。
3.2 二維差分適用場景
圖像處理中的矩形區域調整
例如圖像亮度增強:對 800×600 圖像的 (100,200)~(300,400) 區域亮度 +50。使用 (802×602) 的差分矩陣,直接執行 4 個端點的修改,無需判斷 300+1 或 400+1 是否越界,效率顯著高於逐像素遍歷。
網格地圖的區域狀態更新
例如遊戲地圖的 “技能效果”:在 100×100 的網格中,技能對 (x1,y1)~(x2,y2) 區域的敵人造成傷害。通過 (102×102) 的差分矩陣記錄傷害值,後續計算前綴和即可得到每個敵人的總傷害,避免邊界判斷邏輯。
四、差分算法初始化情況分析
4.1 何時無需初始化?
當原始數組 / 矩陣的初始值為 全 0 時,差分數組 / 矩陣默認初始化為全 0 即可,無需額外操作。例如 “區間加法” 問題中初始數組為全 0,直接使用 new int[length + 1] 初始化差分數組,無需基於原始數組計算初始差分。
4.2 何時需要初始化?
當原始數組 / 矩陣存在 非 0 初始值 時,需將初始狀態轉化為差分更新操作(即 “初始化差分”)。例如原始數組 arr = [3,5,4,6] 或原始矩陣 matrix = [[1,2],[3,4]],需通過遍歷原始數據,對每個元素執行 “單點更新” 操作,構建初始差分數組 / 矩陣。
4.3 二維差分初始化示例(避免邊界判斷)
以 3×3 原始矩陣(1-based)matrix = [[0,0,0,0],[0,1,2,3],[0,4,5,6],[0,7,8,9]](第 0 行第 0 列為佔位符)為例,初始化差分矩陣的過程:
- 差分矩陣尺寸設為 (3+2) × (3+2) = 5×5,初始全 0。
- 對 matrix[1][1] = 1 執行單點更新:diff[1][1] +=1、diff[1][2]-=1、diff[2][1]-=1、diff[2][2]+=1。
- 對 matrix[1][2] = 2 執行單點更新:diff[1][2] +=2、diff[1][3]-=2、diff[2][2]-=2、diff[2][3]+=2。
- 依次遍歷所有元素,最終得到初始差分矩陣。
核心優勢:整個過程無需判斷 i+1 或 j+1 是否超出原始矩陣範圍(如 i=3 時 i+1=4,仍在 5×5 差分矩陣內),代碼簡潔且無越界風險。
五、經典例題
5.1 一維差分
1109. 航班預訂統計 - 力扣(LeetCode)
class Solution {
public int[] corpFlightBookings(int[][] bookings, int n) {
int[] diff = new int[n];
for (int[] booking : bookings) {
int first = booking[0] - 1;
int last = booking[1] - 1;
int seats = booking[2];
// 區間更新
diff[first] += seats;
if (last < diff.length - 1) {
diff[last + 1] -= seats;
}
}
int[] ans = new int[diff.length];
ans[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
ans[i] = ans[i - 1] + diff[i];
}
return ans;
}
}1094. 拼車 - 力扣(LeetCode)
class Solution {
public boolean carPooling(int[][] trips, int capacity) {
int[] diff = new int[1001];
for (int[] trip : trips) {
int num = trip[0];
int from = trip[1];
int to = trip[2];
diff[from] += num;
diff[to] -= num;
}
int res = diff[0];
if (res > capacity)
return false;
for (int i = 1; i < diff.length; i++) {
res = res + diff[i];
if (res > capacity) {
return false;
}
}
return true;
}
}5.2 二維差分
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int q = sc.nextInt();
// 消耗換行符
sc.nextLine();
int[][] matrix = new int[n + 1][m + 1];
for (int i = 1; i <= n; i++) {
String line = sc.nextLine();
for (int j = 1; j <= m; j++) {
char c = line.charAt(j - 1);
if (c == 'B') {
matrix[i][j] = 1;
}
}
}
//n + 2 避免邊界判斷
int [][] diff = new int[n + 2][m + 2];
for(int T = 0;T < q; T++) {
int x1 = sc.nextInt();
int y1 = sc.nextInt();
int x2 = sc.nextInt();
int y2 = sc.nextInt();
//二維差分核心操作
diff[x1][y1] += 1;
diff[x1][y2 + 1] -=1;
diff[x2 + 1][y1] -=1;
diff[x2 + 1][y2 + 1] += 1;
}
int[][] pre = new int[n + 1][m + 1];
int ans = 0;
//差分數組前綴和即為結果數組
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
pre[i][j] = pre[i - 1][j] + pre[i][j - 1]
- pre[i - 1][j - 1] + diff[i][j];
if(pre[i][j] >= 1 || matrix[i][j] == 1) {
ans++;
}
}
}
System.out.println(ans);
}
}