紅黑樹原理和C++實現詳情 - 開發語言,後端,c++,算法,數據結構,JavaScript,前端開發雲端築夢者博客

前言：在計算機科學領域，數據結構的選擇直接決定着算法性能的巔峯。紅黑樹——這一被譽為"最優雅的平衡二叉搜索樹"，憑藉其嚴格的平衡約束和穩定的對數級時間複雜度（O(log n)），已成為高性能系統的核心支柱。從Linux內核的進程調度到C++ STL的map容器，從數據庫引擎的B+樹後備存儲到實時系統的內存管理，紅黑樹的身影無處不在。

一、紅黑樹的定義

二、紅黑樹的性質

三、紅黑樹實現的總體思路

四、紅黑樹的節點結構

五、紅黑樹的插入操作

1.按照二叉搜索的樹規則插入新節點

2.檢測新節點插入後，紅黑樹的性質是否造到破壞

情況一: cur為紅，p為紅，g為黑，u存在且為紅

情況二: cur為紅，p為紅，g為黑，u不存在/u存在且為黑

情況三: cur為紅，p為紅，g為黑，u不存在/u存在且為黑

六、紅黑樹的驗證

總代碼

一、紅黑樹的定義

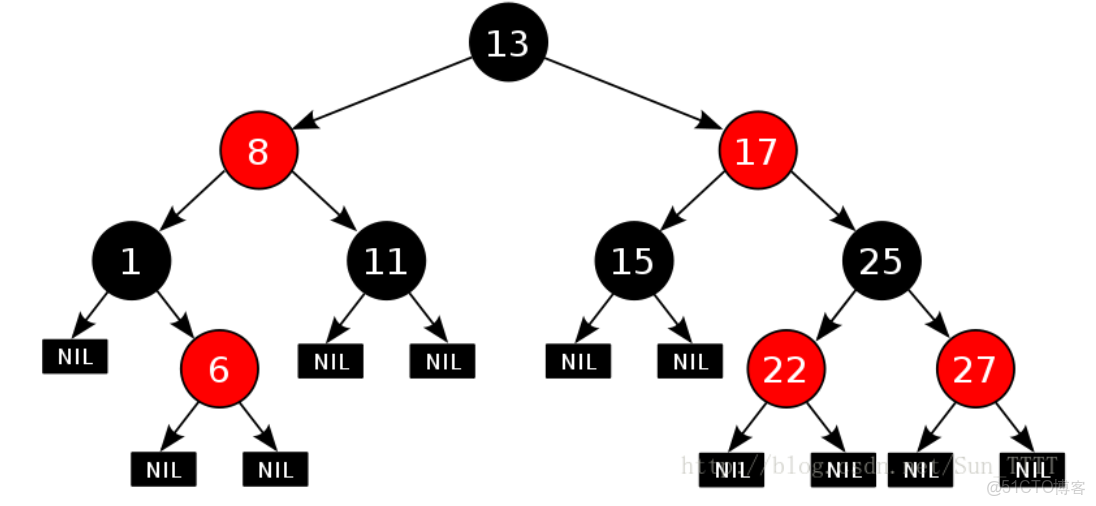
紅黑樹，是一種二叉搜索樹，但在每個結點上增加一個存儲位表示結點的顏色，可以是Red或 Black。通過對任何一條從根到葉子的路徑上各個結點着色方式的限制，紅黑樹確保沒有一條路徑會比其他路徑長出倆倍，因而是接近平衡的。

紅黑樹原理和C++實現_#算法

二、紅黑樹的性質

1.每個結點不是紅色就是黑色

紅黑樹的每個節點都有顏色屬性：紅和黑。不允許出現其它顏色情況

2.根節點是黑色的

整棵紅黑樹的根節點必須是黑色

3.如果一個節點是紅色的，則它的兩個孩子結點是黑色的

也就是説，父子節點不可能出現連續的紅色

4.每個葉子節點都是黑色的

紅黑樹的葉子節點通常定義為 NIL（空節點），即使實際樹中不畫，需視為黑色節點

5.對於每個結點，從該結點到其所有後代葉結點的簡單路徑上，均包含相同數目的黑色結點

簡單路徑：樹中不重複經過節點的路徑（從當前節點到任意葉子節點的路徑唯一）

想象從任意節點出發，沿着所有可能的路徑走向葉子節點（NIL節點），每條路徑經過的黑色節點數量必須完全相同。這個統一的計數被稱為該節點的黑高（Black Height）。

以節點X為起點，可能存在多條通往不同NIL葉子的路徑
路徑可能經過不同數量的紅色節點
但所有路徑中的黑色節點總數必須嚴格一致

B(黑) / \ R(紅) B(黑) / \ / \ NIL NIL NIL NIL

如上代碼，根節點到最左NIL：B→R→NIL（黑高=1）

根節點到最右NIL：B→B→NIL（黑高=2）→ 違反規則（實際紅黑樹不會出現此結構）

黑高的意義是什麼？？

我們前面已經瞭解了，不可能有連續的兩個紅節點，所以一定是一黑一紅，或者兩黑。那麼通過黑高（Black-Height）的嚴格一致，將最長路徑限制在最短路徑的兩倍以內，從而保證樹高始終維持在O(log n)級別。

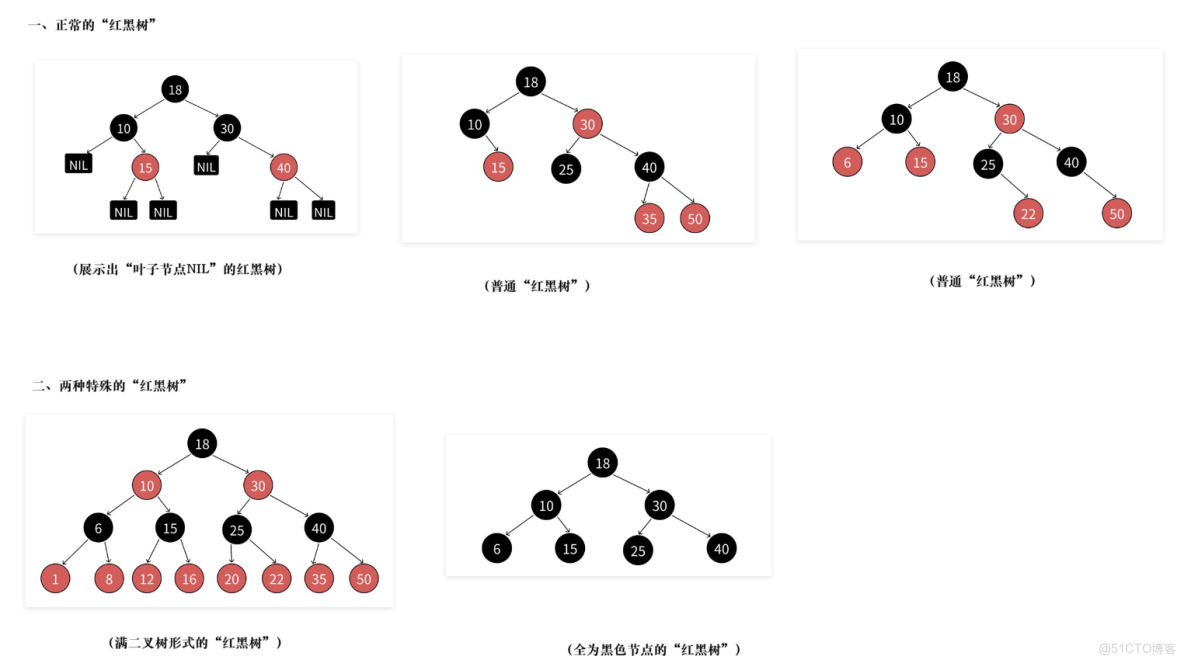
這裏再給大家放一下紅黑樹的各種示意圖，能對性質有更深的理解。

紅黑樹原理和C++實現_#c++_02

正是黑高的存在，所以滿足上面的性質，紅黑樹就能保證：其最長路徑中節點個數不會超過最短路徑節點個數的兩倍。

三、紅黑樹實現的總體思路

紅黑樹包含了之前的AVL樹的四大旋轉，它沒有像AVL樹那樣嚴格的平衡，僅要求：最長路徑不超過最短路徑的兩倍即可。但是插入節點是根據大小選擇性的走左還是走右，我們是無法控制插入位置的，那麼如何保證插入節點後依然屬於紅黑樹？

這裏我們提供三板斧：

1.標準BST插入

按照二叉搜索樹規則找到插入位置，新節點初始設為紅色（最小化對黑高的影響）

設為黑色的代價：必然導致某條路徑黑高+1

需要遞歸調整整棵樹的所有路徑平均需O(log n)次調整

設為紅色的代價：僅可能產生雙紅衝突（父節點也是紅色）

通過有限的旋轉和變色即可修復平均只需O(1)次調整

2.衝突檢測

檢測與父節點的衝突。

3.檢查修復紅黑樹

檢查黑高的改變有沒有影響uncle節點。如有需改變。

四、紅黑樹的節點結構

// 節點顏色：紅或黑
enum Color { RED, BLACK };

// 紅黑樹節點
template<class K, class V>
struct RBTreeNode {
    // 存儲的鍵值對
    std::pair<K, V> kv;
    
    // 節點指針
    RBTreeNode* parent;  // 父節點
    RBTreeNode* left;    // 左孩子
    RBTreeNode* right;   // 右孩子
    
    // 節點顏色
    Color color;         // 顏色標記
    
    // 構造函數
    RBTreeNode(const std::pair<K, V>& kv)
        : kv(kv),         // 初始化鍵值對
          parent(nullptr),// 父節點初始為空
          left(nullptr),  // 左孩子初始為空
          right(nullptr), // 右孩子初始為空
          color(RED)      // 新節點默認紅色（符合紅黑樹規則）
    {}
};

int main() {
    // 創建一個紅黑樹節點
    RBTreeNode<int, std::string> node({10, "Hello"});
    
    // 訪問節點成員
    std::cout << node.kv.first;   // 輸出鍵：10
    std::cout << node.kv.second;  // 輸出值："Hello"
    
    // 檢查節點顏色
    if(node.color == RED) {
        std::cout << "這是紅色節點";
    }
    
    return 0;
}

紅黑樹原理和C++實現_#後端_03

五、紅黑樹的插入操作

首先我們需要先找到那個插入位置：如果是根（顏色為黑）；如果是其它節點（顏色為紅）

1.按照二叉搜索的樹規則插入新節點

// 插入新節點
bool insert(int key, string value) {
    // 1. 如果樹是空的，直接創建根節點
    if (root == nullptr) {
        root = new Node(key, value);
        root->color = BLACK;  // 根節點必須是黑色
        return true;
    }

    // 2. 尋找插入位置
    Node* parent = nullptr;
    Node* current = root;
    
    while (current != nullptr) {
        parent = current;
        
        if (key < current->key) {    // 向左找
            current = current->left;
        } 
        else if (key > current->key) { // 向右找
            current = current->right;
        }
        else {  // 已經存在相同的key
            return false; 
        }
    }

    // 3. 創建新節點（默認為紅色）
    Node* newNode = new Node(key, value);
    newNode->parent = parent;  // 連接父節點
    
    // 4. 連接到父節點
    if (key < parent->key) {
        parent->left = newNode;  // 作為左孩子
    } else {
        parent->right = newNode; // 作為右孩子
    }

    // 5. 這裏應該添加紅黑樹的平衡調整代碼
    // fixInsert(newNode);
    
    return true;
}

2.檢測新節點插入後，紅黑樹的性質是否造到破壞

因為新節點的默認顏色是紅色，因此：如果其雙親節點的顏色是黑色，沒有違反紅黑樹任何
性質，則不需要調整；但當新插入節點的雙親節點顏色為紅色時，就違反了性質三不能有連
在一起的紅色節點，此時需要對紅黑樹分情況來討論：

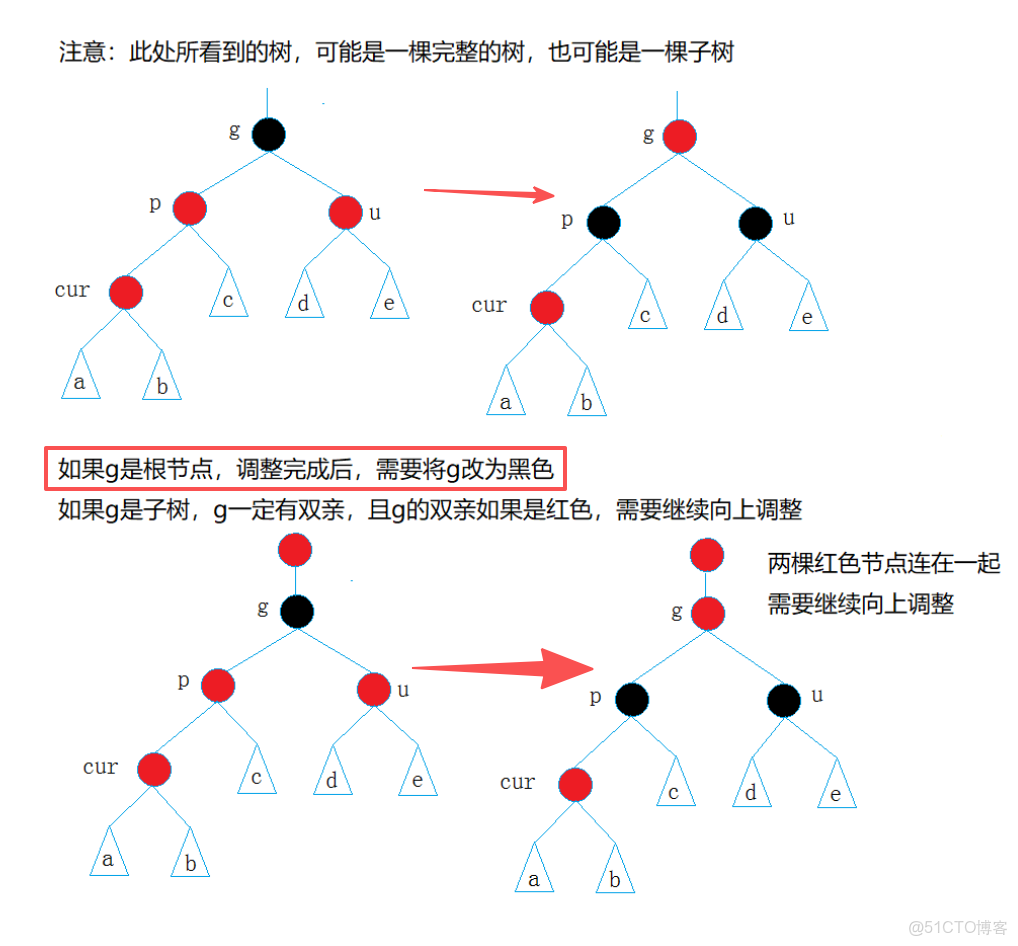
約定:cur為當前節點，p為父節點，g為祖父節點，u為叔叔節點

情況一: cur為紅，p為紅，g為黑，u存在且為紅

紅黑樹原理和C++實現_#算法_04

總結，解決方式：將p,u改為黑，g改為紅，然後把g當成cur，繼續向上調整。

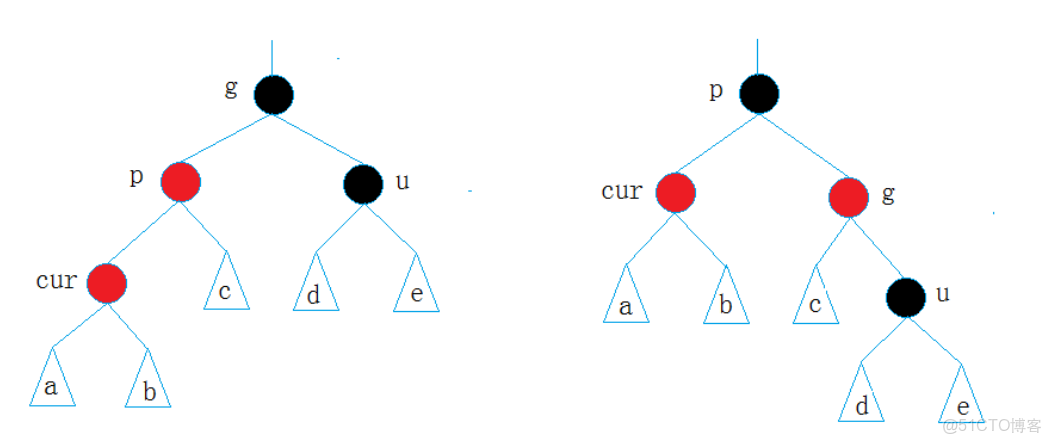
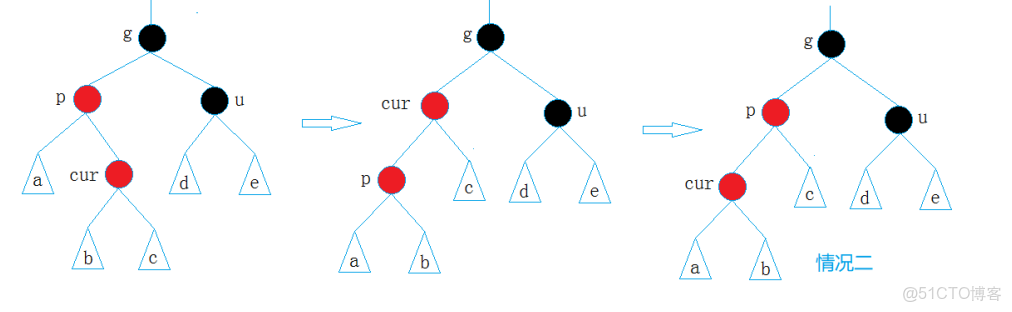
情況二: cur為紅，p為紅，g為黑，u不存在/u存在且為黑

紅黑樹原理和C++實現_#開發語言_05

這裏我們會發現僅靠變色無法修復，因為會導致黑高不一致。必須通過旋轉調整樹結構，再配合變色。也就是右旋再去判斷。

p為g的左孩子，cur為p的左孩子，則進行右單旋轉；

相反， p為g的右孩子，cur為p的右孩子，則進行左單旋轉

p、g變色--p變黑，g變紅

拓展説明：u的情況有兩種
1.如果u節點不存在，則cur一定是新插入節點，因為如果cur不是新插入節點，
則cur和p一定有一個節點的顏色是黑色，就不滿足性質4：每條路徑黑色節點個
數相同。
2.如果u節點存在，則其一定是黑色的，那麼cur節點原來的顏色一定是黑色的，
現在看到其是紅色的原因是因為cur的子樹在調整的過程中將cur節點的顏色由
黑色改成紅色。

🔍 為什麼u不存在時cur一定是新插入節點？

黑(g) / \ 紅(p) NIL(黑) / 紅(cur) ← 新插入節點

如果cur不是新插入的節點，而u是NIL（黑色），那麼從祖父節點g出發：

路徑1：g → p → cur → NIL

路徑2：g → u（NIL）

路徑1的黑高：g(1) → p(不算) → cur(不算) → NIL(1) → 總計：2

路徑2的黑高：g(1) → NIL(1) → 總計：2

如果cur原本就存在且為黑色：

黑(g) / \ 紅(p) NIL(黑) / 黑(cur) ← 違反性質4！

路徑1黑高：g(1) → p(不算) → cur(1) → NIL(1) → 總計：3
路徑2黑高：g(1) → NIL(1) → 總計：2

所以不可能，結論：只有當cur是新插入節點時，才可能遇到u不存在的情況

🔍 為什麼cur"原來的顏色"是黑色？
這裏的"原來"指的是在插入新節點前的狀態。考慮紅黑樹的性質：

每次插入新節點時都設為紅色（初始紅色）
如果cur不是新插入節點，那麼它之前一定是黑色節點被改為紅色，這就説明，u存在的時候，一定是自下而上調整成為黑色的。

情況三: cur為紅，p為紅，g為黑，u不存在/u存在且為黑

紅黑樹原理和C++實現_#後端_06

p為g的左孩子，cur為p的右孩子，則針對p做左單旋轉；相反， p為g的右孩子，cur為p的左孩子，則針對p做右單旋轉即可

六、紅黑樹的驗證

我們來根據下面幾個性質檢測紅黑樹：

根節點是否為黑色

是否有連續的紅色節點

根據任意一條路徑的黑色節點去測一棵樹的黑高，看是否相等

總代碼

#include <iostream>
#include <utility>
using namespace std;

// 節點顏色：紅或黑
enum Color { RED, BLACK };

// 紅黑樹節點
template<class K, class V>
struct RBTreeNode {
    // 存儲的鍵值對
    pair<K, V> kv;

    // 節點指針
    RBTreeNode* parent;  // 父節點
    RBTreeNode* left;    // 左孩子
    RBTreeNode* right;   // 右孩子

    // 節點顏色
    Color color;         // 顏色標記

    // 構造函數
    RBTreeNode(const pair<K, V>& kv)
        : kv(kv),         // 初始化鍵值對
        parent(nullptr),  // 父節點初始為空
        left(nullptr),    // 左孩子初始為空
        right(nullptr),   // 右孩子初始為空
        color(RED)        // 新節點默認紅色（符合紅黑樹規則）
    {}
};

// 紅黑樹類
template<class K, class V>
class RBTree {
public:
    typedef RBTreeNode<K, V> Node;
    Node* root = nullptr;

    // 插入鍵值對
    bool insert(const K& key, const V& value) {
        // 1. 如果樹是空的，直接創建根節點
        if (root == nullptr) {
            root = new Node(make_pair(key, value));
            root->color = BLACK;  // 根節點必須是黑色
            return true;
        }

        // 2. 尋找插入位置
        Node* parent = nullptr;
        Node* current = root;

        while (current != nullptr) {
            parent = current;

            if (key < current->kv.first) {    // 向左找
                current = current->left;
            }
            else if (key > current->kv.first) { // 向右找
                current = current->right;
            }
            else {  // 已經存在相同的key
                return false;
            }
        }

        // 3. 創建新節點（默認為紅色）
        Node* newNode = new Node(make_pair(key, value));
        newNode->parent = parent;  // 連接父節點

        // 4. 連接到父節點
        if (key < parent->kv.first) {
            parent->left = newNode;  // 作為左孩子
        }
        else {
            parent->right = newNode; // 作為右孩子
        }

        // 5. 平衡調整
        fixInsert(newNode);

        return true;
    }

    // 左旋
    void rotateLeft(Node* x) {
        Node* y = x->right;
        x->right = y->left;
        
        if (y->left != nullptr) {
            y->left->parent = x;
        }
        
        y->parent = x->parent;
        
        if (x->parent == nullptr) {
            root = y;
        } else if (x == x->parent->left) {
            x->parent->left = y;
        } else {
            x->parent->right = y;
        }
        
        y->left = x;
        x->parent = y;
    }

    // 右旋
    void rotateRight(Node* y) {
        Node* x = y->left;
        y->left = x->right;
        
        if (x->right != nullptr) {
            x->right->parent = y;
        }
        
        x->parent = y->parent;
        
        if (y->parent == nullptr) {
            root = x;
        } else if (y == y->parent->left) {
            y->parent->left = x;
        } else {
            y->parent->right = x;
        }
        
        x->right = y;
        y->parent = x;
    }

    // 插入後修復紅黑樹性質
    void fixInsert(Node* z) {
        while (z != root && z->parent->color == RED) {
            if (z->parent == z->parent->parent->left) {
                Node* y = z->parent->parent->right;
                if (y != nullptr && y->color == RED) {
                    // 情況1：叔叔是紅色
                    z->parent->color = BLACK;
                    y->color = BLACK;
                    z->parent->parent->color = RED;
                    z = z->parent->parent;
                } else {
                    if (z == z->parent->right) {
                        // 情況2：叔叔是黑色，z是右孩子
                        z = z->parent;
                        rotateLeft(z);
                    }
                    // 情況3：叔叔是黑色，z是左孩子
                    z->parent->color = BLACK;
                    z->parent->parent->color = RED;
                    rotateRight(z->parent->parent);
                }
            } else {
                Node* y = z->parent->parent->left;
                if (y != nullptr && y->color == RED) {
                    // 情況1鏡像
                    z->parent->color = BLACK;
                    y->color = BLACK;
                    z->parent->parent->color = RED;
                    z = z->parent->parent;
                } else {
                    if (z == z->parent->left) {
                        // 情況2鏡像
                        z = z->parent;
                        rotateRight(z);
                    }
                    // 情況3鏡像
                    z->parent->color = BLACK;
                    z->parent->parent->color = RED;
                    rotateLeft(z->parent->parent);
                }
            }
        }
        root->color = BLACK;
    }

    // 中序遍歷打印樹
    void inorderTraversal(Node* node) {
        if (node == nullptr) return;
        inorderTraversal(node->left);
        cout << node->kv.first << "(" << (node->color == RED ? "R" : "B") << ") ";
        inorderTraversal(node->right);
    }

    // 打印樹結構
    void printTree() {
        inorderTraversal(root);
        cout << endl;
    }
};

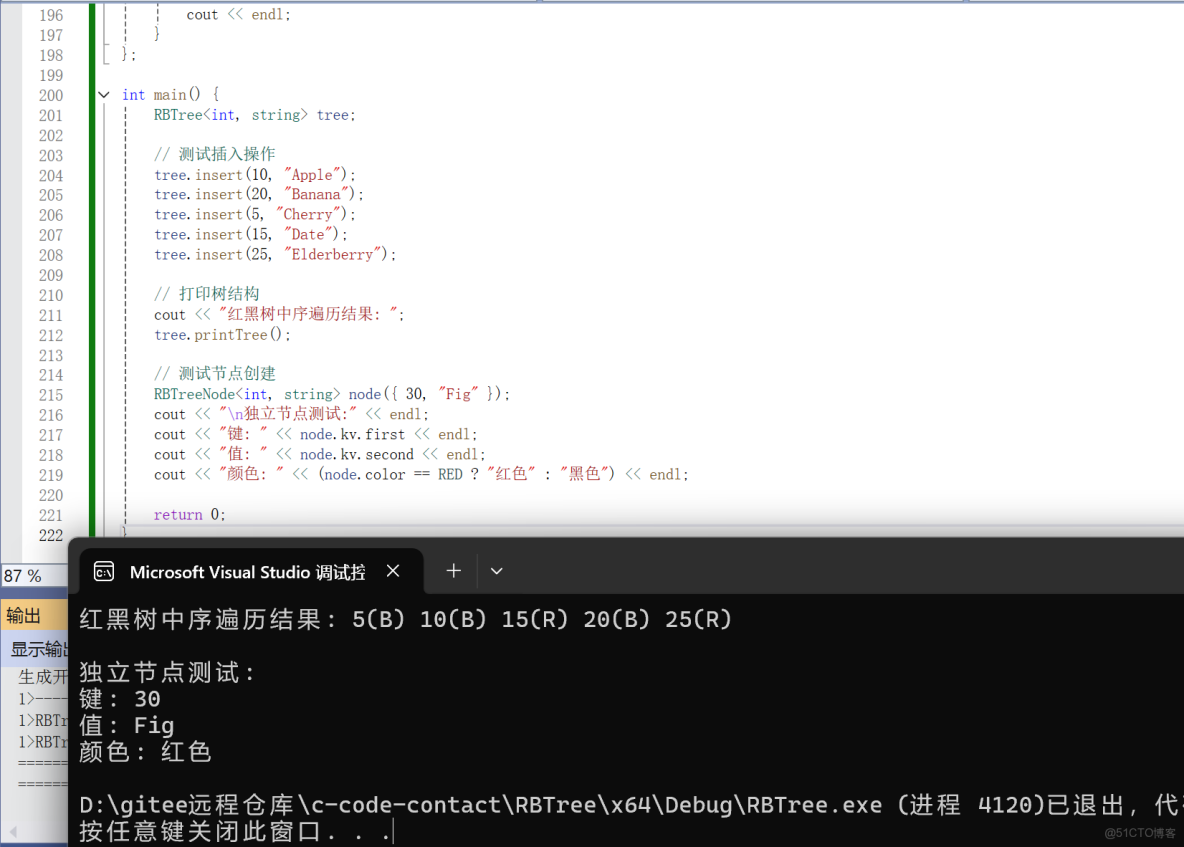
int main() {
    RBTree<int, string> tree;
    
    // 測試插入操作
    tree.insert(10, "Apple");
    tree.insert(20, "Banana");
    tree.insert(5, "Cherry");
    tree.insert(15, "Date");
    tree.insert(25, "Elderberry");
    
    // 打印樹結構
    cout << "紅黑樹中序遍歷結果: ";
    tree.printTree();
    
    // 測試節點創建
    RBTreeNode<int, string> node({30, "Fig"});
    cout << "\n獨立節點測試:" << endl;
    cout << "鍵: " << node.kv.first << endl;
    cout << "值: " << node.kv.second << endl;
    cout << "顏色: " << (node.color == RED ? "紅色" : "黑色") << endl;
    
    return 0;
}

紅黑樹原理和C++實現_#數據結構_07