此篇一區論文。一個圖回憶長啥樣

 

至於模型就省略了吧，注意挖空部分使用可是材料ecth。

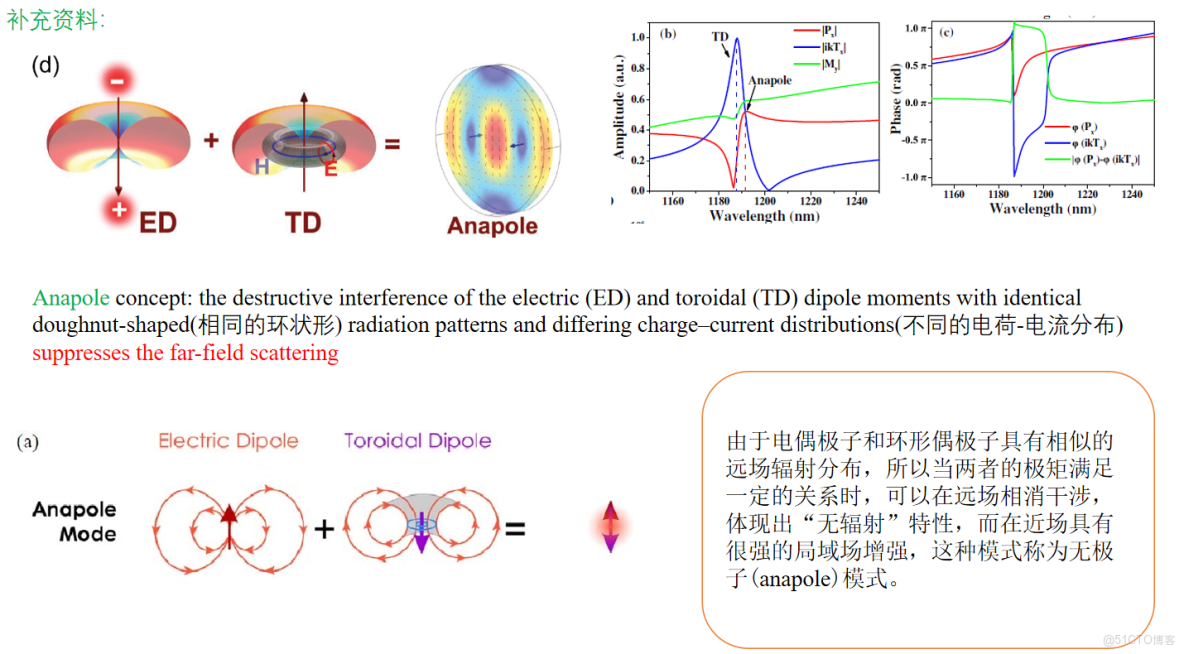
在這一篇，我們能接觸到的新概念有 無極子， BIC與準BIC， 束縛能力， 環形模式的優勢， 折射率與紅藍移的關係，調製深度。

 

一、無極子

 

二、BIC與準BIC

BIC是一種諧振狀態，線寬接近於0。

準BIC就是原本沒有峯，由於不對稱導致能量泄露，出現了峯？（不知道這麼理解可以不？）

 

 

 三、束縛能力

我們希望結構有很強的場束縛能力（低損耗，弱自由空間耦合，弱輻射，對吧？）

論文中經常提到的“自由空間”指的是結構的表面周圍，在周圍長增強很大。

“自由空間”泛指比較遠的地方。

 

四、環形模式的優勢

 

環形模式的高品質因數並非來自非對稱性或BIC，而是由於環形模式與自由空間的固有弱耦合以及每個諧振器之間的強近場耦合引起的。

從製造容差的角度來看，這種機制優於基於不對稱的方法。

具體地，通過不對稱獲得的Q因數與結構的不對稱量成反比，並且最終受制造期間可行的長度尺度限制。

簡言之就是，實際容易操作，固有優勢。

五、折射率與紅藍移的關係

n低------藍移

 

六、調製深度

調製深度 = 峯的透射率T —— 谷的透射率T

調製深度有什麼意義呢？