一、實驗題目
102.二叉樹的層序遍歷
給你二叉樹的根節點 root ,返回其節點值的 層序遍歷 。 (即逐層地,從左到右訪問所有節點)。
面試題08.10.顏色填充
編寫函數,實現許多圖片編輯軟件都支持的「顏色填充」功能。 待填充的圖像用二維數組 image 表示,元素為初始顏色值。初始座標點的行座標為 sr 列座標為 sc。需要填充的新顏色為 newColor 。 「周圍區域」是指顏色相同且在上、下、左、右四個方向上存在相連情況的若干元素。 請用新顏色填充初始座標點的周圍區域,並返回填充後的圖像。
LCR 150.
彩燈裝飾記錄2
一棵聖誕樹記作根節點為 root 的二叉樹,節點值為該位置裝飾彩燈的顏色編號。請按照從左到右的順序返回每一層彩燈編號,每一層的結果記錄於一行。
765.情侶牽手
n 對情侶坐在連續排列的 2n 個座位上,想要牽到對方的手。 人和座位由一個整數數組 row 表示,其中 row[i] 是坐在第 i 個座位上的人的 ID。情侶們按順序編號,第一對是 (0, 1),第二對是 (2, 3),以此類推,最後一對是 (2n-2, 2n-1)。 返回 最少交換座位的次數,以便每對情侶可以並肩坐在一起。 每次交換可選擇任意兩人,讓他們站起來交換座位。
二、實驗思路和方案
102.二叉樹的層序遍歷
題目要求的二叉樹的從上至下打印(即按層打印),又稱為二叉樹的廣度優先搜索。廣度優先搜索通常藉助隊列的先入先出特性來實現。
將本層全部節點打印到一行,並將下一層全部節點加入隊列,以此類推,即可分為多行打印。
面試題08.10.顏色填充
可以將與指定節點相鄰的,且顏色相同,且不等於新顏色的節點加入隊列Queue中,然後依次取出再進行處理。
LCR 150.彩燈裝飾記錄2
在二叉樹層序遍歷的基礎上,這道題要求將每層打印到一行。因此我們可以考慮將當前全部節點打印到一行,並將下一層全部節點加入隊列,以此類推,即可分為多行打印。
765.情侶牽手
首先將節點都標記為未訪問,並遍歷圖中的每個節點。如果發現一個未訪問的節點,就從該節點出發,沿着圖中的邊,將其餘的未訪問的節點都標記為已訪問,並同時統計標記的次數。當遍歷過程終止時,標記的數量次數即為連通分量的大小。
三、實驗代碼
102.二叉樹的層序遍歷
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
List<List<Integer>> res = new ArrayList<>();
if (root != null) queue.add(root);
while (!queue.isEmpty()) {
List<Integer> tmp = new ArrayList<>();
for(int i = queue.size(); i > 0; i--) {
TreeNode node = queue.poll();
tmp.add(node.val);
if (node.left != null) queue.add(node.left);
if (node.right != null) queue.add(node.right);
}
res.add(tmp);
}
return res;
}
}
面試題08.10.顏色填充
class Solution {
public int[][] floodFill(int[][] image, int sr, int sc, int newColor) {
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[]{sr, sc});
int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
while (!queue.isEmpty()) {
int[] arr = queue.poll();
int i = arr[0];
int j = arr[1];
int oldColor = image[i][j];
image[i][j] = newColor;
for (int k = 0; k < dir.length; k++) {
int r = dir[k][0] + i;
int c = dir[k][1] + j;
if (r >= 0 && r < image.length && c >= 0 && c < image[0].length && image[r][c] == oldColor && image[r][c] != newColor) {
queue.offer(new int[]{r, c});
}
}
}
return image;
}
}
LCR 150.彩燈裝飾記錄2
class Solution {
public List<List<Integer>> decorateRecord(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
List<List<Integer>> res = new ArrayList<>();
if (root != null) queue.add(root);
while (!queue.isEmpty()) {
List<Integer> tmp = new ArrayList<>();
for (int i = queue.size(); i > 0; i--) {
TreeNode node = queue.poll();
tmp.add(node.val);
if (node.left != null) queue.add(node.left);
if (node.right != null) queue.add(node.right);
}
res.add(tmp);
}
return res;
}
}
765.情侶牽手
class Solution {
public int minSwapsCouples(int[] row) {
int m = row.length;
int n = m / 2;
List<Integer>[] graph = new List[n];
for (int i = 0; i < n; ++i) {
graph[i] = new ArrayList<>();
}
for (int i = 0; i < m; i += 2) {
int x = row[i] / 2, y = row[i + 1] / 2;
if (x != y) {
graph[x].add(y);
graph[y].add(x);
}
}
boolean[] visited = new boolean[n];
int res = 0;
for (int i = 0; i < n; ++i) {
if (!visited[i]) {
Queue<Integer> queue = new LinkedList<>();
visited[i] = true;
queue.offer(i);
int cnt = 0;
while (!queue.isEmpty()) {
int x = queue.poll();
++cnt;
for (int y : graph[x]) {
if (!visited[y]) {
visited[y] = true;
queue.offer(y);
}
}
}
res += cnt - 1;
}
}
return res;
}
}四、實驗結果及分析
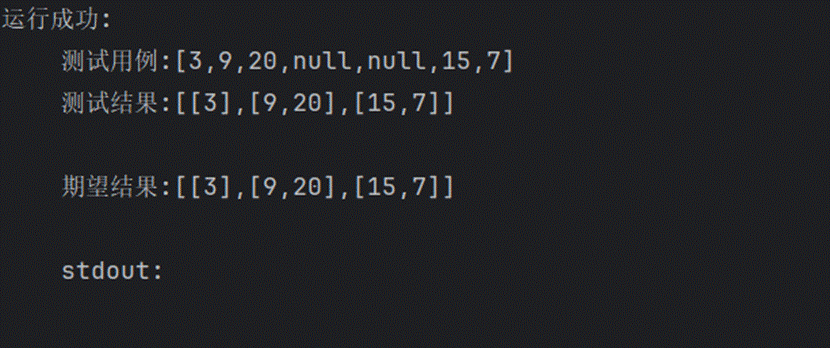
102.二叉樹的層序遍歷
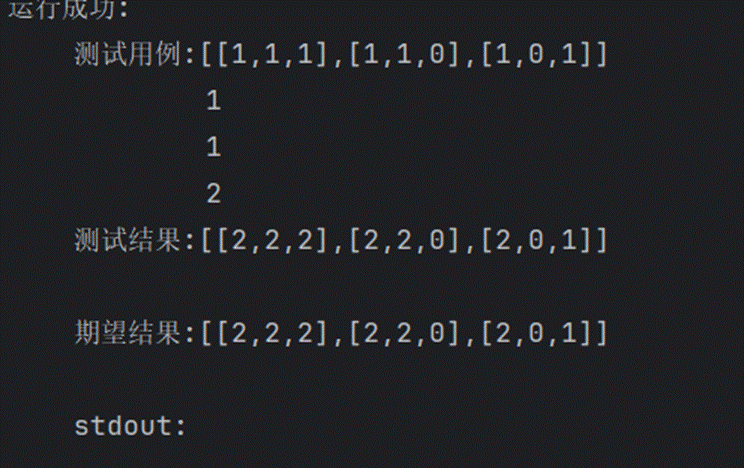
面試題08.10.顏色填充
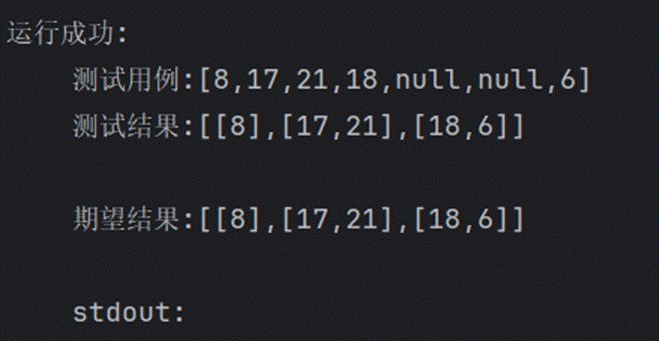
LCR 150.彩燈裝飾記錄2
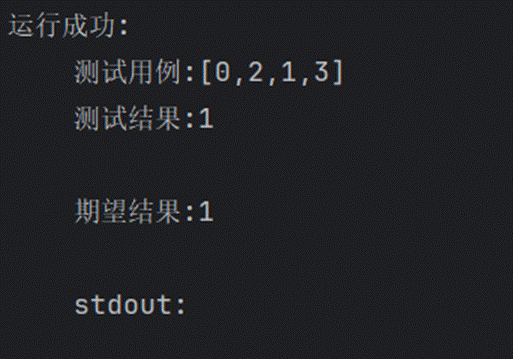
765.情侶牽手
五、實驗總結及體會
通過本次實驗,我對廣度優先搜索有了初步的理解和認識。廣度優先搜索適用於無權重圖的最短路徑和狀態空間搜索,但在狀態空間過大時可能會導致內存溢出。