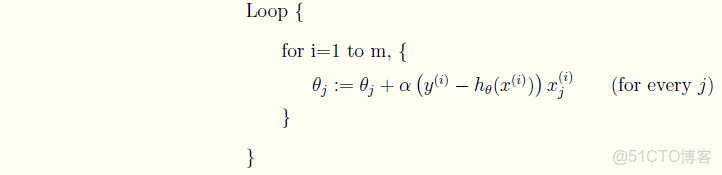本文主要講了梯度下降法的兩種迭代思路,隨機梯度下降(Stochastic gradient descent)和批量梯度下降(Batch gradient descent)。以及他們在python中的實現。
梯度下降法
梯度下降是一個最優化算法,通俗的來講也就是沿着梯度下降的方向來求出一個函數的極小值。那麼我們在高等數學中學過,對於一些我們瞭解的函數方程,我們可以對其求一階導和二階導,比如説二次函數。可是我們在處理問題的時候遇到的並不都是我們熟悉的函數,並且既然是機器學習就應該讓機器自己去學習如何對其進行求解,顯然我們需要換一個思路。因此我們採用梯度下降,不斷迭代,沿着梯度下降的方向來移動,求出極小值。
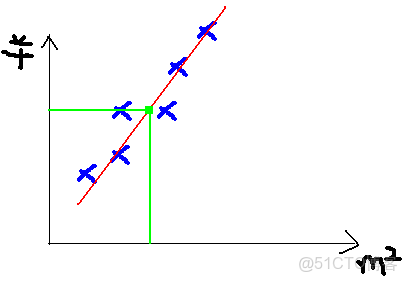
此處我們還是用coursea的機器學習課中的案例,假設我們從中介那裏拿到了一個地區的房屋售價表,那麼在已知房子面積的情況下,如何得知房子的銷售價格。顯然,這是一個線性模型,房子面積是自變量x,銷售價格是因變量y。我們可以用給出的數據畫一張圖。然後,給出房子的面積,就可以從圖中得知房子的售價了。
現在我們的問題就是,針對給出的數據,如何得到一條最擬合的直線。
對於線性模型,如下。
- h(x)是需要擬合的函數。
- J(θ)稱為均方誤差或cost function。用來衡量訓練集眾的樣本對線性模式的擬合程度。
- m為訓練集眾樣本的個數。
- θ是我們最終需要通過梯度下降法來求得的參數。
h(θ)=∑j=0nθjxjJ(θ)=12m∑i=0m(yi−hθ(xi))2h(θ)=∑j=0nθjxjJ(θ)=12m∑i=0m(yi−hθ(xi))2
接下來的梯度下降法就有兩種不同的迭代思路。
批量梯度下降(Batch gradient descent)
現在我們就要求出J(θ)取到極小值時的θTθT向量。之前已經説過了,沿着函數梯度的反方向下降就能最快的找到極小值。
- 計算J(θ)關於θTθT的偏導數,也就得到了向量中每一個θθ的梯度。
∂J(θ)∂θj=−1m∑i=0m(yi−hθ(xi))∂∂θj(yi−hθ(xi))=−1m∑i=0m(yi−hθ(xi))∂∂θj(∑j=0nθjxij−yi)=−1m∑i=0m(yi−hθ(xi))xij(1)(2)(3)(1)∂J(θ)∂θj=−1m∑i=0m(yi−hθ(xi))∂∂θj(yi−hθ(xi))(2)=−1m∑i=0m(yi−hθ(xi))∂∂θj(∑j=0nθjxji−yi)(3)=−1m∑i=0m(yi−hθ(xi))xji - 沿着梯度的反方向更新參數θ的值
θj:=θj+α∂J(θ)∂θj:=θj−α1m∑i=0m(yi−hθ(xi))xijθj:=θj+α∂J(θ)∂θj:=θj−α1m∑i=0m(yi−hθ(xi))xji - 迭代直到收斂。
可以看到,批量梯度下降是用了訓練集中的所有樣本。因此在數據量很大的時候,每次迭代都要遍歷訓練集一遍,開銷會很大,所以在數據量大的時候,可以採用隨機梯度下降法。
隨機梯度下降(Stochastic gradient descent)
和批量梯度有所不同的地方在於,每次迭代只選取一個樣本的數據,一旦到達最大的迭代次數或是滿足預期的精度,就停止。
可以得出隨機梯度下降法的θ更新表達式。
θj:=θj−α1m(yi−hθ(xi))xijθj:=θj−α1m(yi−hθ(xi))xji
迭代直到收斂。
兩種迭代思路的python實現
下面是python的代碼實現,現在僅僅是用純python的語法(python2.7)來實現的。隨着學習的深入,屆時還會有基於numpy等一些庫的實現,下次補充。
#encoding:utf-8
#隨機梯度
def stochastic_gradient_descent(x,y,theta,alpha,m,max_iter):
"""隨機梯度下降法,每一次梯度下降只使用一個樣本。
:param x: 訓練集種的自變量
:param y: 訓練集種的因變量
:param theta: 待求的權值
:param alpha: 學習速率
:param m: 樣本總數
:param max_iter: 最大迭代次數
"""
deviation = 1
iter = 0
flag = 0
while True:
for i in range(m): #循環取訓練集中的一個
deviation = 0
h = theta[0] * x[i][0] + theta[1] * x[i][1]
theta[0] = theta[0] + alpha * (y[i] - h)*x[i][0]
theta[1] = theta[1] + alpha * (y[i] - h)*x[i][1]
iter = iter + 1
#計算誤差
for i in range(m):
deviation = deviation + (y[i] - (theta[0] * x[i][0] + theta[1] * x[i][1])) ** 2
if deviation <EPS or iter >max_iter:
flag = 1
break
if flag == 1 :
break
return theta, iter
#批量梯度
def batch_gradient_descent(x,y,theta,alpha,m,max_iter):
"""批量梯度下降法,每一次梯度下降使用訓練集中的所有樣本來計算誤差。
:param x: 訓練集種的自變量
:param y: 訓練集種的因變量
:param theta: 待求的權值
:param alpha: 學習速率
:param m: 樣本總數
:param max_iter: 最大迭代次數
"""
deviation = 1
iter = 0
while deviation > EPS and iter < max_iter:
deviation = 0
sigma1 = 0
sigma2 = 0
for i in range(m): #對訓練集中的所有數據求和迭代
h = theta[0] * x[i][0] + theta[1] * x[i][1]
sigma1 = sigma1 + (y[i] - h)*x[i][0]
sigma2 = sigma2 + (y[i] - h)*x[i][1]
theta[0] = theta[0] + alpha * sigma1 /m
theta[1] = theta[1] + alpha * sigma2 /m
#計算誤差
for i in range(m):
deviation = deviation + (y[i] - (theta[0] * x[i][0] + theta[1] * x[i][1])) ** 2
iter = iter + 1
return theta, iter
#運行 為兩種算法設置不同的參數
# data and init
matrix_x = [[2.1,1.5],[2.5,2.3],[3.3,3.9],[3.9,5.1],[2.7,2.7]]
matrix_y = [2.5,3.9,6.7,8.8,4.6]
MAX_ITER = 5000
EPS = 0.0001
#隨機梯度
theta = [2,-1]
ALPHA = 0.05
resultTheta,iters = stochastic_gradient_descent(matrix_x, matrix_y, theta, ALPHA, 5, MAX_ITER)
print 'theta=',resultTheta
print 'iters=',iters
#批量梯度
theta = [2,-1]
ALPHA = 0.05
resultTheta,iters = batch_gradient_descent(matrix_x, matrix_y, theta, ALPHA, 5, MAX_ITER)
print 'theta=',resultTheta
print 'iters=',iters
#encoding:utf-8
#隨機梯度
def stochastic_gradient_descent(x,y,theta,alpha,m,max_iter):
"""隨機梯度下降法,每一次梯度下降只使用一個樣本。
:param x: 訓練集種的自變量
:param y: 訓練集種的因變量
:param theta: 待求的權值
:param alpha: 學習速率
:param m: 樣本總數
:param max_iter: 最大迭代次數
"""
deviation = 1
iter = 0
flag = 0
while True:
for i in range(m): #循環取訓練集中的一個
deviation = 0
h = theta[0] * x[i][0] + theta[1] * x[i][1]
theta[0] = theta[0] + alpha * (y[i] - h)*x[i][0]
theta[1] = theta[1] + alpha * (y[i] - h)*x[i][1]
iter = iter + 1
#計算誤差
for i in range(m):
deviation = deviation + (y[i] - (theta[0] * x[i][0] + theta[1] * x[i][1])) ** 2
if deviation <EPS or iter >max_iter:
flag = 1
break
if flag == 1 :
break
return theta, iter
#批量梯度
def batch_gradient_descent(x,y,theta,alpha,m,max_iter):
"""批量梯度下降法,每一次梯度下降使用訓練集中的所有樣本來計算誤差。
:param x: 訓練集種的自變量
:param y: 訓練集種的因變量
:param theta: 待求的權值
:param alpha: 學習速率
:param m: 樣本總數
:param max_iter: 最大迭代次數
"""
deviation = 1
iter = 0
while deviation > EPS and iter < max_iter:
deviation = 0
sigma1 = 0
sigma2 = 0
for i in range(m): #對訓練集中的所有數據求和迭代
h = theta[0] * x[i][0] + theta[1] * x[i][1]
sigma1 = sigma1 + (y[i] - h)*x[i][0]
sigma2 = sigma2 + (y[i] - h)*x[i][1]
theta[0] = theta[0] + alpha * sigma1 /m
theta[1] = theta[1] + alpha * sigma2 /m
#計算誤差
for i in range(m):
deviation = deviation + (y[i] - (theta[0] * x[i][0] + theta[1] * x[i][1])) ** 2
iter = iter + 1
return theta, iter
#運行 為兩種算法設置不同的參數
# data and init
matrix_x = [[2.1,1.5],[2.5,2.3],[3.3,3.9],[3.9,5.1],[2.7,2.7]]
matrix_y = [2.5,3.9,6.7,8.8,4.6]
MAX_ITER = 5000
EPS = 0.0001
#隨機梯度
theta = [2,-1]
ALPHA = 0.05
resultTheta,iters = stochastic_gradient_descent(matrix_x, matrix_y, theta, ALPHA, 5, MAX_ITER)
print 'theta=',resultTheta
print 'iters=',iters
#批量梯度
theta = [2,-1]
ALPHA = 0.05
resultTheta,iters = batch_gradient_descent(matrix_x, matrix_y, theta, ALPHA, 5, MAX_ITER)
print 'theta=',resultTheta
print 'iters=',iters
代碼見github。https://github.com/maoqyhz/machine_learning_practice.git 運行結果
ALPHA = 0.05
theta= [-0.08445285887795494, 1.7887820818368738]
iters= 1025
theta= [-0.08388979324755381, 1.7885951009289043]
iters= 772
[Finished in 0.5s]ALPHA = 0.01
theta= [-0.08387216503392847, 1.7885649678753883]
iters= 3566
theta= [-0.08385924864202322, 1.788568071697816]
iters= 3869
[Finished in 0.1s]ALPHA = 0.1
theta= [588363545.9596066, -664661366.4562845]
iters= 5001
theta= [-0.09199523483489512, 1.7944581778450577]
iters= 516
[Finished in 0.2s]總結
梯度下降法是一種最優化問題求解的算法。有批量梯度和隨機梯度兩種不同的迭代思路。他們有以下的差異:
- 批量梯度收斂速度慢,隨機梯度收斂速度快。
- 批量梯度是在θ更新前對所有樣例彙總誤差,而隨機梯度下降的權值是通過考查某個樣本來更新的
- 批量梯度的開銷大,隨機梯度的開銷小。
使用梯度下降法時需要尋找出一個最好的學習效率。這樣可以使得使用最少的迭代次數達到我們需要的精度。
##################################################
最小二乘法與梯度下降法區別
最小二乘法跟梯度下降法都是通過求導來求損失函數的最小值,那它們有什麼區別呢。
相同