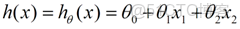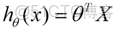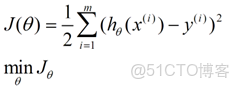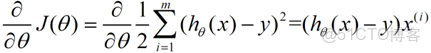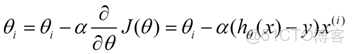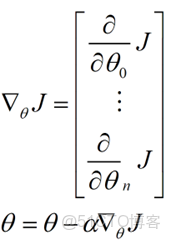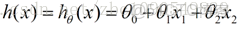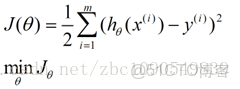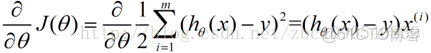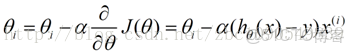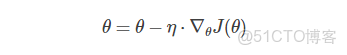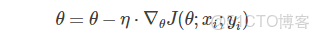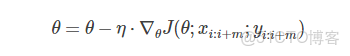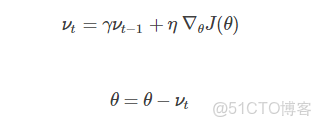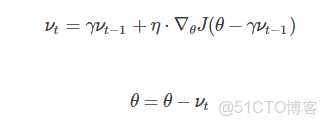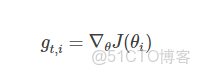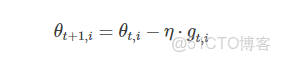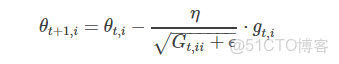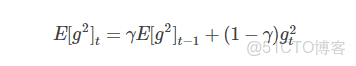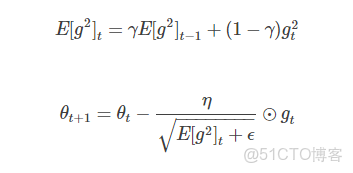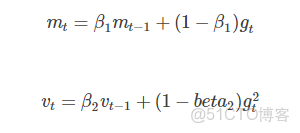迴歸與梯度下降

　　迴歸在數學上來説是給定一個點集，能夠用一條曲線去擬合之，如果這個曲線是一條直線，那就被稱為線性迴歸，如果曲線是一條二次曲線，就被稱為二次迴歸，迴歸還有很多的變種，如本地加權迴歸、邏輯迴歸，等等。

　　用一個很簡單的例子來説明迴歸，這個例子來自很多的地方，也在很多的開源軟件中看到，比如説weka。大概就是，做一個房屋價值的評估系統，一個房屋的價值來自很多地方，比如説面積、房間的數量（幾室幾廳）、地 段、朝向等等，這些影響房屋價值的變量被稱為特徵(feature)，feature在機器學習中是一個很重要的概念，有很多的論文專門探討這個東西。在 此處，為了簡單，假設我們的房屋就是一個變量影響的，就是房屋的面積。

　　假設有一個房屋銷售的數據如下：

　　面積(m^2)  銷售價錢（萬元）

　　123            250

　　150            320

　　87              160

　　102            220

　　…               …

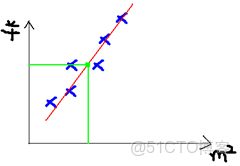
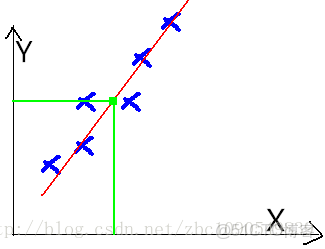
　　這個表類似於帝都5環左右的房屋價錢，我們可以做出一個圖，x軸是房屋的面積。y軸是房屋的售價，如下：

　　如果來了一個新的面積，假設在銷售價錢的記錄中沒有的，我們怎麼辦呢？

　　我們可以用一條曲線去儘量準的擬合這些數據，然後如果有新的輸入過來，我們可以在將曲線上這個點對應的值返回。如果用一條直線去擬合，可能是下面的樣子：

　　綠色的點就是我們想要預測的點。

　　首先給出一些概念和常用的符號，在不同的機器學習書籍中可能有一定的差別。

　　房屋銷售記錄表 - 訓練集(training set)或者訓練數據(training data), 是我們流程中的輸入數據，一般稱為x

　　房屋銷售價錢 - 輸出數據，一般稱為y

　　擬合的函數（或者稱為假設或者模型），一般寫做 y = h(x)

　　訓練數據的條目數(#training set), 一條訓練數據是由一對輸入數據和輸出數據組成的

　　輸入數據的維度(特徵的個數，#features)，n

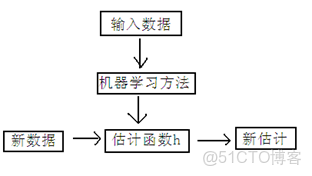
　　下面是一個典型的機器學習的過程，首先給出一個輸入數據，我們的算法會通過一系列的過程得到一個估計的函數，這個函數有能力對沒有見過的新數據給出一個新的估計，也被稱為構建一個模型。就如同上面的線性迴歸函數。

　　我們用X1，X2..Xn 去描述feature裏面的分量，比如x1=房間的面積，x2=房間的朝向，等等，我們可以做出一個估計函數：

　　θ在這兒稱為參數，在這兒的意思是調整feature中每個分量的影響力，就是到底是房屋的面積更重要還是房屋的地段更重要。為了如果我們令X0 = 1，就可以用向量的方式來表示了：

　　我們程序也需要一個機制去評估我們θ是否比較好，所以説需要對我們做出的h函數進行評估，一般這個函數稱為損失函數（loss function）或者錯誤函數(error function)，描述h函數不好的程度，在下面，我們稱這個函數為J函數

　　在這兒我們可以做出下面的一個錯誤函數：

　　這個錯誤估計函數是去對x(i)的估計值與真實值y(i)差的平方和作為錯誤估計函數，前面乘上的1/2是為了在求導的時候，這個係數就不見了。

　　如何調整θ以使得J(θ)取得最小值有很多方法，其中有最小二乘法(min square)，是一種完全是數學描述的方法，在stanford機器學習開放課最後的部分會推導最小二乘法的公式的來源，這個來很多的機器學習和數學書 上都可以找到，這裏就不提最小二乘法，而談談梯度下降法。

梯度下降法是按下面的流程進行

　　1）首先對θ賦值，這個值可以是隨機的，也可以讓θ是一個全零的向量。

　　2）改變θ的值，使得J(θ)按梯度下降的方向進行減少。

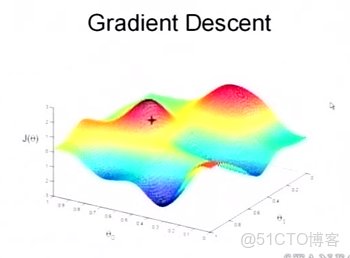
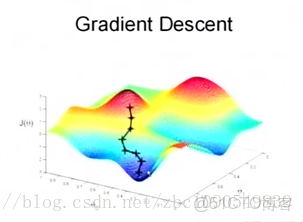
　　為了更清楚，給出下面的圖：

　　這是一個表示參數θ與誤差函數J(θ)的關係圖，紅色的部分是表示J(θ)有着比較高的取值，我們需要的是，能夠讓J(θ)的值儘量的低。也就是深藍色的部分。θ0，θ1表示θ向量的兩個維度。

　　在上面提到梯度下降法的第一步是給θ給一個初值，假設隨機給的初值是在圖上的十字點。

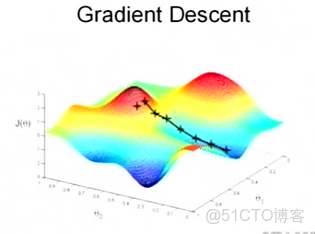
　　然後我們將θ按照梯度下降的方向進行調整，就會使得J(θ)往更低的方向進行變化，如圖所示，算法的結束將是在θ下降到無法繼續下降為止。

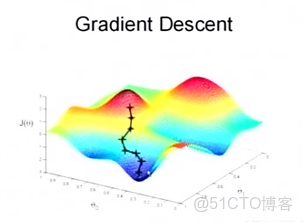
　　當然，可能梯度下降的最終點並非是全局最小點，可能是一個局部最小點，可能是下面的情況：

　　上面這張圖就是描述的一個局部最小點，這是我們重新選擇了一個初始點得到的，看來我們這個算法將會在很大的程度上被初始點的選擇影響而陷入局部最小點

　　　下面我將用一個例子描述一下梯度減少的過程，對於我們的函數J(θ)求偏導J：（求導的過程如果不明白，可以温習一下微積分）

　　下面是更新的過程，也就是θi會向着梯度最小的方向進行減少。θi表示更新之前的值，-後面的部分表示按梯度方向減少的量，α表示步長，也就是每次按照梯度減少的方向變化多少。

　　一個很重要的地方值得注意的是，梯度是有方向的，對於一個向量θ，每一維分量θi都可以求出一個梯度的方向，我們就可以找到一個整體的方向，在變化的時候，我們就朝着下降最多的方向進行變化就可以達到一個最小點，不管它是局部的還是全局的。

　　用更簡單的數學語言進行描述步驟2）是這樣的：

　　倒三角形表示梯度，按這種方式來表示，θi就不見了，看看用好向量和矩陣，真的會大大的簡化數學的描述啊。

誤差準則函數與隨機梯度下降

　　數學一點將就是，對於給定的一個點集（X，Y），找到一條曲線或者曲面，對其進行擬合之。同時稱X中的變量為特徵（Feature)，Y值為預測值。

　　如圖：

　　一個典型的機器學習的過程，首先給出一組輸入數據X，我們的算法會通過一系列的過程得到一個估計的函數，這個函數有能力對沒有見過的新數據給出一個新的估計Y，也被稱為構建一個模型。

　　我們用X1、X2...Xn 去描述feature裏面的分量，用Y來描述我們的估計，得到一下模型：

　　我們需要一種機制去評價這個模型對數據的描述到底夠不夠準確，而採集的數據x、y通常來説是存在誤差的（多數情況下誤差服從高斯分佈），於是，自然的，引入誤差函數：

　　關鍵的一點是如何調整theta值，使誤差函數J最小化。J函數構成一個曲面或者曲線，我們的目的是找到該曲面的最低點：

　　假設隨機站在該曲面的一點，要以最快的速度到達最低點，我們當然會沿着坡度最大的方向往下走（梯度的反方向）。

　　用數學描述就是一個求偏導數的過程：

　　這樣，參數theta的更新過程描述為以下：

         （α表示算法的學習速率）

不同梯度下降算法的區別

　梯度下降：全量梯度下降就是我上面的推導，要留意，在梯度下降中，對於θθ的更新，所有的樣本都有貢獻，也就是參與調整θθ.其計算得到的是一個標準梯度。因而理論上來説一次更新的幅度是比較大的。如果樣本不多的情況下，當然是這樣收斂的速度會更快啦。

　　隨機梯度下降：可以看到多了隨機兩個字，隨機也就是説我用樣本中的一個例子來近似我所有的樣本，來調整θθ，因而隨機梯度下降是會帶來一定的問題，因為計算得到的並不是準確的一個梯度，容易陷入到局部最優解中。

　　批量梯度下降：其實批量的梯度下降就是一種折中的方法，他用了一些小樣本來近似全部的，其本質就是我1個指不定不太準，那我用個30個50個樣本那比隨機的要準不少了吧，而且批量的話還是非常可以反映樣本的一個分佈情況的。

　　 隨機梯度下降和批量梯度下降都是梯度下降方法的一種，都是通過求偏導的方式求參數的最優解。

　　批量梯度下降算法：是通過對每一個樣本求偏導，然後挨個更新。（對於大樣本的實驗，這種方法效率太低）。

　　而隨機梯度下降算法則是從其中的所有樣本中取出部分樣本求偏導，對參數進行更新。

梯度下降算法是機器學習中使用非常廣泛的優化算法，也是眾多機器學習算法中最常用的優化方法。幾乎當前每一個先進的(state-of-the-art)機器學習庫或者深度學習庫都會包括梯度下降算法的不同變種實現。但是，它們就像一個黑盒優化器，很難得到它們優缺點的實際解釋。 

梯度下降算法是通過沿着目標函數J(θ)參數θ∈R的梯度(一階導數)相反方向−∇θJ(θ)來不斷更新模型參數來到達目標函數的極小值點（收斂），更新步長為η。

三種梯度下降優化框架

   有三種梯度下降算法框架，它們不同之處在於每次學習(更新模型參數)使用的樣本個數，每次更新使用不同的樣本會導致每次學習的準確性和學習時間不同。

1、全量梯度下降(Batch gradient descent) 
   每次使用全量的訓練集樣本來更新模型參數，即： 

　　 其Python代碼如下：

for i in range(epochs):
    params_grad = evaluate_gradient(loss_function,data,params)
    params = params - learning_rate * params_grad

　　epochs 是用户輸入的最大迭代次數。通過上訴代碼可以看出，每次使用全部訓練集樣本計算損失函數loss_function的梯度params_grad，然後使用學習速率learning_rate朝着梯度相反方向去更新模型的每個參數params。一般各現有的一些機器學習庫都提供了梯度計算api。如果想自己親手寫代碼計算，那麼需要在程序調試過程中驗證梯度計算是否正確。

　　全量梯度下降每次學習都使用整個訓練集，因此其優點在於每次更新都會朝着正確的方向進行，最後能夠保證收斂於極值點(凸函數收斂於全局極值點，非凸函數可能會收斂於局部極值點)，但是其缺點在於每次學習時間過長，並且如果訓練集很大以至於需要消耗大量的內存，並且全量梯度下降不能進行在線模型參數更新。

　2、隨機梯度下降(Stochastic gradient descent)

   隨機梯度下降算法每次從訓練集中隨機選擇一個樣本來進行學習，即： 

　　 批量梯度下降算法每次都會使用全部訓練樣本，因此這些計算是冗餘的，因為每次都使用完全相同的樣本集。而隨機梯度下降算法每次只隨機選擇一個樣本來更新模型參數，因此每次的學習是非常快速的，並且可以進行在線更新。 
   其Python代碼如下：

for i in range(epochs):
    np.random.shuffle(data)
    for example in data:
        params_grad = evaluate_gradient(loss_function,example,params)
        params = params - learning_rate * params_grad

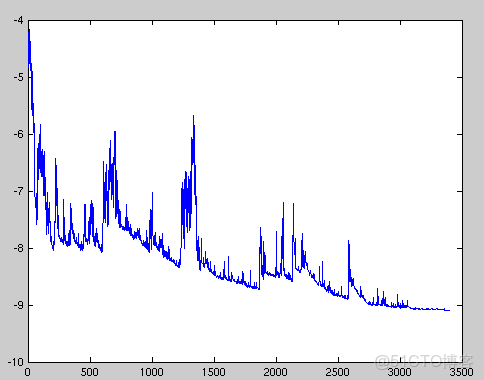
隨機梯度下降最大的缺點在於每次更新可能並不會按照正確的方向進行，因此可以帶來優化波動(擾動)，如下圖：

　　 不過從另一個方面來看，隨機梯度下降所帶來的波動有個好處就是，對於類似盆地區域（即很多局部極小值點）那麼這個波動的特點可能會使得優化的方向從當前的局部極小值點跳到另一個更好的局部極小值點，這樣便可能對於非凸函數，最終收斂於一個較好的局部極值點，甚至全局極值點。 
   由於波動，因此會使得迭代次數（學習次數）增多，即收斂速度變慢。不過最終其會和全量梯度下降算法一樣，具有相同的收斂性，即凸函數收斂於全局極值點，非凸損失函數收斂於局部極值點。

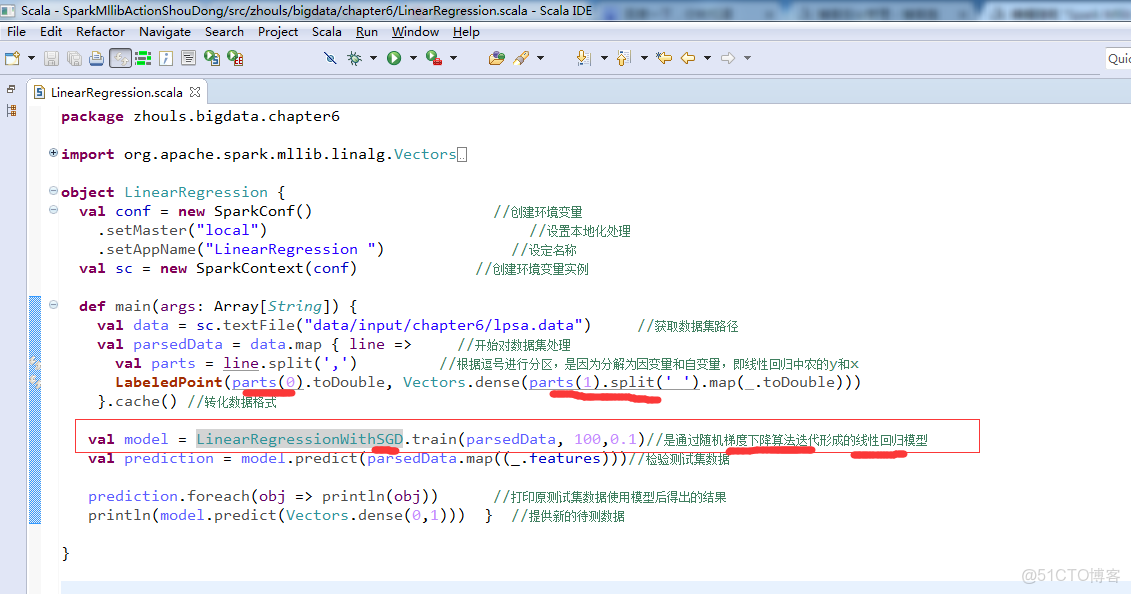
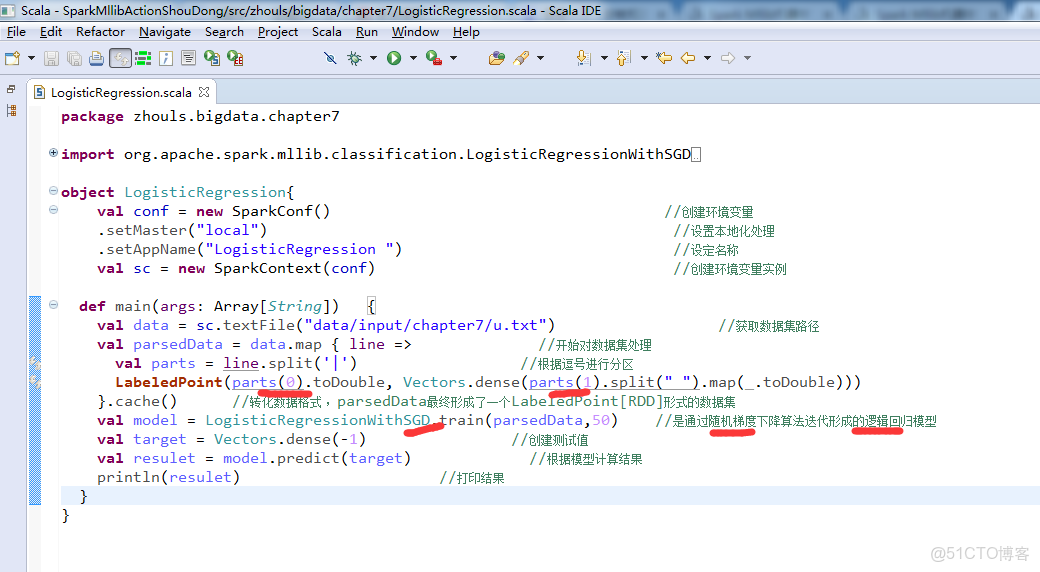
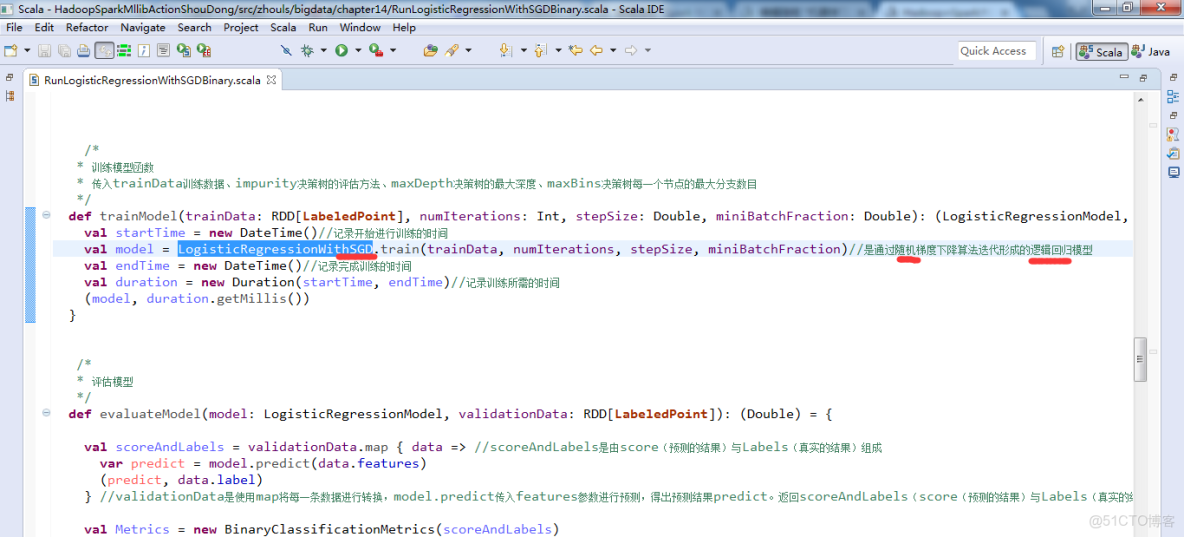
隨機梯度下降算法迭代形成的邏輯迴歸模型  和   通過隨機梯度下降算法迭代形成的線性迴歸模型

　　具體見

Spark Mllib機器學習實戰的第6章 線性迴歸理論與實戰

 　　具體，見

Spark Mllib機器學習實戰的第7章 Mllib分類實戰

　　具體，見

Hadoop+Spark大數據巨量分析與機器學習整合開發實戰的第14章 使用邏輯迴歸二元分類算法來預測分類StumbleUpon數據集

3、小批量梯度下降算法(Mini-batch gradient descent)

m，m < n個樣本進行學習，即： 

　　 其Python代碼如下：

for i in range(epochs):
    np.random.shuffle(data)
    for batch in get_batches(data, batch_size=50):
        params_grad = evaluate_gradient(loss_function,batch,params)
        params = params - learning_rate * params_grad

　　相對於隨機梯度下降算法，小批量梯度下降算法降低了收斂波動性，即降低了參數更新的方差，使得更新更加穩定。相對於全量梯度下降，其提高了每次學習的速度。並且其不用擔心內存瓶頸從而可以利用矩陣運算進行高效計算。一般而言每次更新隨機選擇[50,256]個樣本進行學習，但是也要根據具體問題而選擇，實踐中可以進行多次試驗，選擇一個更新速度與更次次數都較適合的樣本數。

   mini-batch梯度下降雖然可以保證收斂性。mini-batch梯度下降常用於神經網絡中。

梯度下降算法的問題與挑戰

 　　雖然梯度下降算法效果很好，並且廣泛使用，但同時其也存在一些挑戰與問題需要解決：

• 選擇一個合理的學習速率很難。如果學習速率過小，則會導致收斂速度很慢。如果學習速率過大，那麼其會阻礙收斂，即在極值點附近會振盪。
• 學習速率調整(又稱學習速率調度，Learning rate schedules試圖在每次更新過程中，改變學習速率，如退火。一般使用某種事先設定的策略或者在每次迭代中衰減一個較小的閾值。無論哪種調整方法，都需要事先進行固定設置，這邊便無法自適應每次學習的數據集特點。
• 模型所有的參數每次更新都是使用相同的學習速率。如果數據特徵是稀疏的或者每個特徵有着不同的取值統計特徵與空間，那麼便不能在每次更新中每個參數使用相同的學習速率，那些很少出現的特徵應該使用一個相對較大的學習速率。
• 對於非凸目標函數，容易陷入那些次優的局部極值點中，如在神經網路中。那麼如何避免呢。Dauphin指出更嚴重的問題不是局部極值點，而是鞍點(These saddle points are usually surrounded by a plateau of the same error, which makes it notoriously hard for SGD to escape, as the gradient is close to zero in all dimensions.)。

梯度下降優化算法

　　下面將討論一些在深度學習社區中經常使用用來解決上訴問題的一些梯度優化方法，不過並不包括在高維數據中不可行的算法，如牛頓法。

　　1、Momentum

   如果在峽谷地區(某些方向較另一些方向上陡峭得多，常見於局部極值點)，SGD會在這些地方附近振盪，從而導致收斂速度慢。這種情況下，動量(Momentum)便可以解決。動量在參數更新項中加上一次更新量(即動量項),即： 

γ<1 ，一般是小於等於0.9。

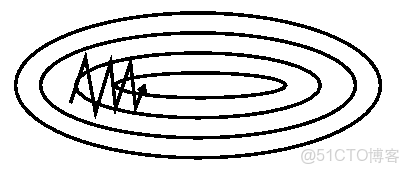
　　其作用如下圖所示： 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  圖    沒有動量 

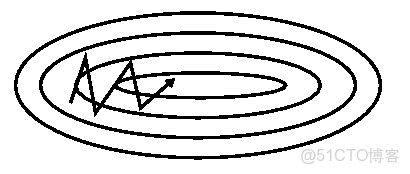
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 圖    加上動量

 　　加上動量項就像從山頂滾下一個球，求往下滾的時候累積了前面的動量(動量不斷增加)，因此速度變得越來越快，直到到達終點。同理，在更新模型參數時，對於那些當前的梯度方向與上一次梯度方向相同的參數，那麼進行加強，即這些方向上更快了；對於那些當前的梯度方向與上一次梯度方向不同的參數，那麼進行削減，即這些方向上減慢了。因此可以獲得更快的收斂速度與減少振盪。

2、NAG

 　　從山頂往下滾的球會盲目地選擇斜坡。更好的方式應該是在遇到傾斜向上之前應該減慢速度。 
   Nesterov accelerated gradient(NAG,涅斯捷羅夫梯度加速)不僅增加了動量項，並且在計算參數的梯度時，在損失函數中減去了動量項，即計算∇θJ(θ−γνt−1)，這種方式預估了下一次參數所在的位置。即： 

 
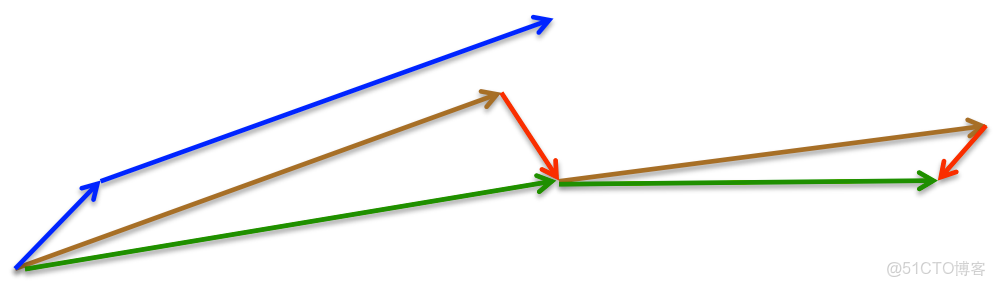
　　如下圖所示： 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　圖   NAG更新

γ=0.9，首先計算當前梯度項，如上圖小藍色向量，然後加上動量項，這樣便得到了大的跳躍，如上圖大藍色的向量。這便是隻包含動量項的更新。而NAG首先來一個大的跳躍（動量項)，然後加上一個小的使用了動量計算的當前梯度（上圖紅色向量）進行修正得到上圖綠色的向量。這樣可以阻止過快更新來提高響應性，如在RNNs中。 
   通過上面的兩種方法，可以做到每次學習過程中能夠根據損失函數的斜率做到自適應更新來加速SGD的收斂。下一步便需要對每個參數根據參數的重要性進行各自自適應更新。

　　3、Adagrad

   Adagrad[3]也是一種基於梯度的優化算法，它能夠對每個參數自適應不同的學習速率，對稀疏特徵，得到大的學習更新，對非稀疏特徵，得到較小的學習更新，因此該優化算法適合處理稀疏特徵數據。Dean等發現Adagrad能夠很好的提高SGD的魯棒性，google便用起來訓練大規模神經網絡(看片識貓:recognize cats in Youtube videos)。Pennington等在GloVe中便使用Adagrad來訓練得到詞向量(Word Embeddings), 頻繁出現的單詞賦予較小的更新，不經常出現的單詞則賦予較大的更新。 
   在前述中，每個模型參數θi使用相同的學習速率η，而Adagrad在每一個更新步驟中對於每一個模型參數θi使用不同的學習速率ηi，設第t次更新步驟中，目標函數的參數θi梯度為gt,i，即： 

  　　那麼SGD更新方程為： 

　　而Adagrad對每一個參數使用不同的學習速率，其更新方程為：

  　　Adagrad主要優勢在於它能夠為每個參數自適應不同的學習速率，而一般的人工都是設定為0.01。同時其缺點在於需要計算參數梯度序列平方和，並且學習速率趨勢是不斷衰減最終達到一個非常小的值。下文中的Adadelta便是用來解決該問題的。

w；二是對於參數梯度歷史窗口序列(不包括當前)不再使用平方和，而是使用均值代替；三是最終的均值是歷史窗口序列均值與當前梯度的時間衰減加權平均。即：

γ與動量項中的一樣，都是

　　RMSprop

   其實RMSprop是Adadelta的中間形式，也是為了降低Adagrad中學習速率衰減過快問題，即： 

γ=0.9,η=0.001

　　Adam

   Adaptive Moment Estimation(Adam) 也是一種不同參數自適應不同學習速率方法，與Adadelta與RMSprop區別在於，它計算曆史梯度衰減方式不同，不使用歷史平方衰減，其衰減方式類似動量，如下：

mt與vt分別是梯度的帶權平均和帶權有偏方差，初始為0向量，Adam的作者發現他們傾向於0向量(接近於0向量)，特別是在衰減因子(衰減率)β1,β2接近於1時。為了改進這個問題，對mt與vt進行偏差修正(bias-corrected)： 

β1=0.9，β2=0.999，ϵ=10−8。論文中將Adam與其它的幾個自適應學習速率進行了比較，效果均要好。

各優化方法比較

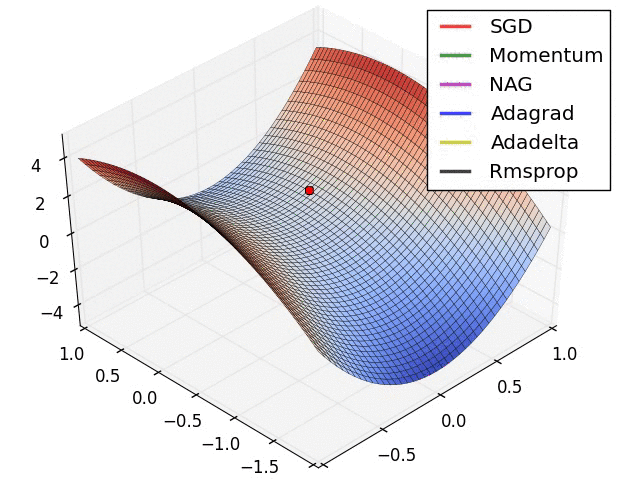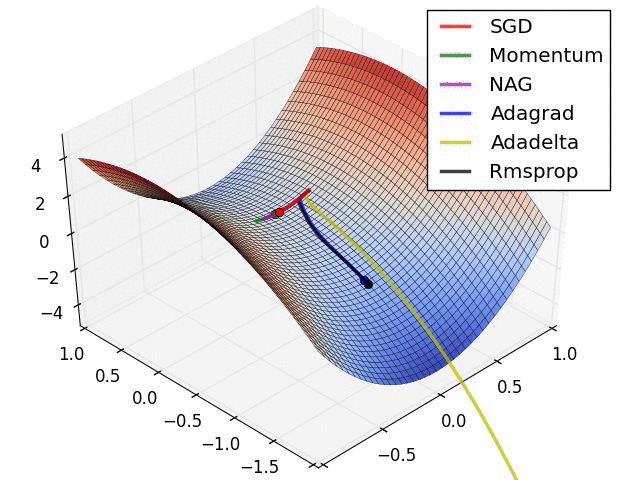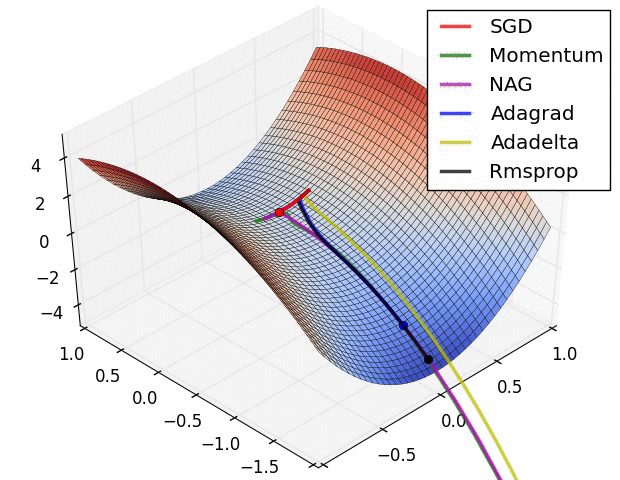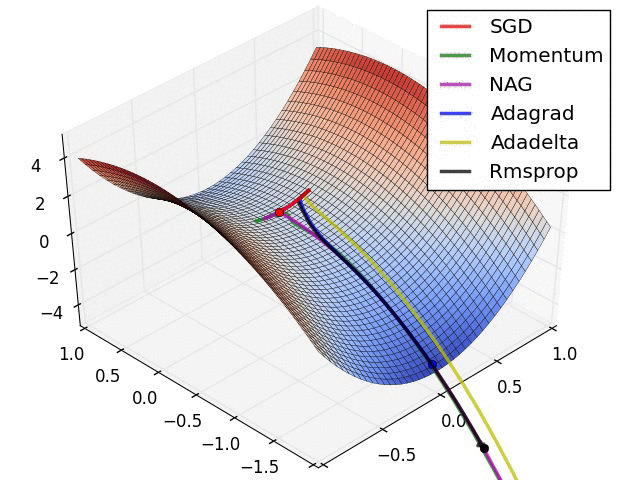
   下面兩幅圖可視化形象地比較上述各優化方法，詳細參見這裏，如圖： 

　　　　　　　　　　　　圖   SGD各優化方法在損失曲面上的表現

　　 從上圖可以看出， Adagrad、Adadelta與RMSprop在損失曲面上能夠立即轉移到正確的移動方向上達到快速的收斂。而Momentum 與NAG會導致偏離(off-track)。同時NAG能夠在偏離之後快速修正其路線，因為其根據梯度修正來提高響應性。 

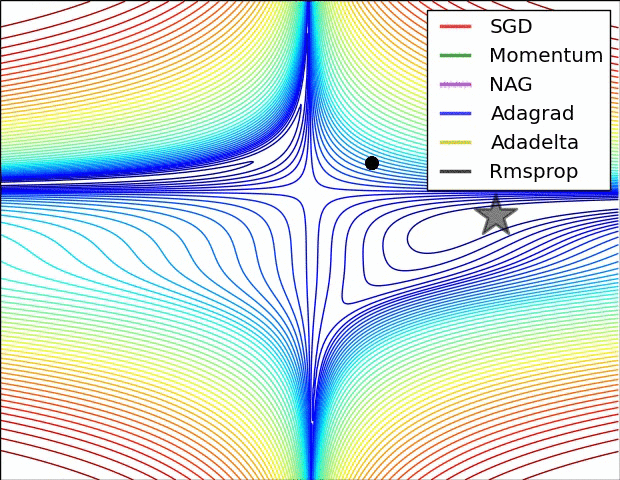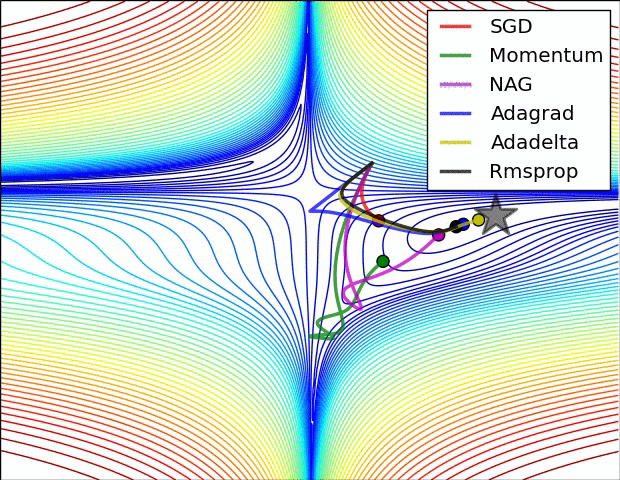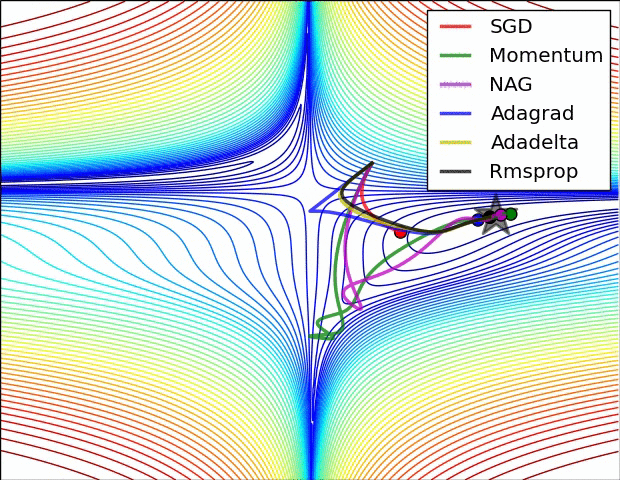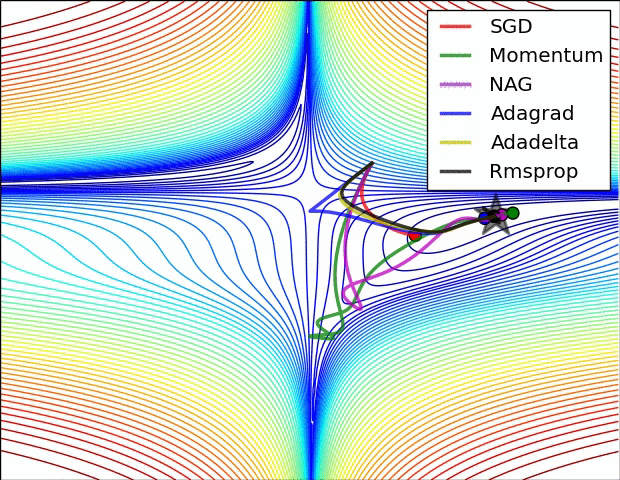
　　　　　　　　　　　　　　　　　　　　圖   SGD各優化方法在損失曲面鞍點處上的表現

   從上圖可以看出，在鞍點（saddle points）處(即某些維度上梯度為零，某些維度上梯度不為零)，SGD、Momentum與NAG一直在鞍點梯度為零的方向上振盪，很難打破鞍點位置的對稱性；Adagrad、RMSprop與Adadelta能夠很快地向梯度不為零的方向上轉移。 
   從上面兩幅圖可以看出，自適應學習速率方法(Adagrad、Adadelta、RMSprop與Adam)在這些場景下具有更好的收斂速度與收斂性。

如何選擇SGD優化器

   如果你的數據特徵是稀疏的，那麼你最好使用自適應學習速率SGD優化方法(Adagrad、Adadelta、RMSprop與Adam)，因為你不需要在迭代過程中對學習速率進行人工調整。 
   RMSprop是Adagrad的一種擴展，與Adadelta類似，但是改進版的Adadelta使用RMS去自動更新學習速率，並且不需要設置初始學習速率。而Adam是在RMSprop基礎上使用動量與偏差修正。RMSprop、Adadelta與Adam在類似的情形下的表現差不多。Kingma[15]指出收益於偏差修正，Adam略優於RMSprop，因為其在接近收斂時梯度變得更加稀疏。因此，Adam可能是目前最好的SGD優化方法。 
   有趣的是，最近很多論文都是使用原始的SGD梯度下降算法，並且使用簡單的學習速率退火調整（無動量項）。現有的已經表明：SGD能夠收斂於最小值點，但是相對於其他的SGD，它可能花費的時間更長，並且依賴於魯棒的初始值以及學習速率退火調整策略，並且容易陷入局部極小值點，甚至鞍點。因此，如果你在意收斂速度或者訓練一個深度或者複雜的網絡，你應該選擇一個自適應學習速率的SGD優化方法。

並行與分佈式SGD

   如果你處理的數據集非常大，並且有機器集羣可以利用，那麼並行或分佈式SGD是一個非常好的選擇，因為可以大大地提高速度。SGD算法的本質決定其是串行的(step-by-step)。因此如何進行異步處理便是一個問題。雖然串行能夠保證收斂，但是如果訓練集大，速度便是一個瓶頸。如果進行異步更新，那麼可能會導致不收斂。下面將討論如何進行並行或分佈式SGD，並行一般是指在同一機器上進行多核並行，分佈式是指集羣處理。

• Hogwild 
     Niu[23]提出了被稱為Hogwild的並行SGD方法。該方法在多個CPU時間進行並行。處理器通過共享內存來訪問參數，並且這些參數不進行加鎖。它為每一個cpu分配不重疊的一部分參數（分配互斥），每個cpu只更新其負責的參數。該方法只適合處理數據特徵是稀疏的。該方法幾乎可以達到一個最優的收斂速度，因為cpu之間不會進行相同信息重寫。
• Downpour SGD 
     Downpour SGD是Dean[4]提出的在DistBelief(Google TensorFlow的前身)使用的SGD的一個異步變種。它在訓練子集上訓練同時多個模型副本。這些副本將各自的更新發送到參數服務器(PS,parameter server)，每個參數服務器只更新互斥的一部分參數，副本之間不會進行通信。因此可能會導致參數發散而不利於收斂。
• Delay-tolerant Algorithms for SGD 
     McMahan與Streeter[12]擴展AdaGrad，通過開發延遲容忍算法(delay-tolerant algorithms)，該算法不僅自適應過去梯度，並且會更新延遲。該方法已經在實踐中表明是有效的。
• TensorFlow 
     TensorFlow[13]是Google開源的一個大規模機器學習庫，它的前身是DistBelief。它已經在大量移動設備上或者大規模分佈式集羣中使用了，已經經過了實踐檢驗。其分佈式實現是基於圖計算，它將圖分割成多個子圖，每個計算實體作為圖中的一個計算節點，他們通過Rend/Receive來進行通信。具體參見這裏。
• Elastic Averaging SGD 
     Zhang等[14]提出Elastic Averaging SGD(EASGD)，它通過一個elastic force(存儲參數的參數服務器中心）來連接每個work來進行參數異步更新。This allows the local variables to fluctuate further from the center variable, which in theory allows for more exploration of the parameter space. They show empirically that this increased capacity for exploration leads to improved performance by finding new local optima. 這句話不太懂，需要去看論文。

更多的SGD優化策略

   接下來介紹更多的SGD優化策略來進一步提高SGD的性能。另外還有眾多其它的優化策略，可以參見[22]。

• Shuffling and Curriculum Learning 
     為了使得學習過程更加無偏，應該在每次迭代中隨機打亂訓練集中的樣本。 
     另一方面，在很多情況下，我們是逐步解決問題的，而將訓練集按照某個有意義的順序排列會提高模型的性能和SGD的收斂性，如何將訓練集建立一個有意義的排列被稱為Curriculum Learning[16]。 
     Zaremba與Sutskever[17]在使用Curriculum Learning來訓練LSTMs以解決一些簡單的問題中，表明一個相結合的策略或者混合策略比對訓練集按照按照訓練難度進行遞增排序要好。（表示不懂，衰）
• Batch normalization 
     為了方便訓練，我們通常會對參數按照0均值1方差進行初始化，隨着不斷訓練，參數得到不同程度的更新，這樣這些參數會失去0均值1方差的分佈屬性，這樣會降低訓練速度和放大參數變化隨着網絡結構的加深。 
     Batch normalization[18]在每次mini-batch反向傳播之後重新對參數進行0均值1方差標準化。這樣可以使用更大的學習速率，以及花費更少的精力在參數初始化點上。Batch normalization充當着正則化、減少甚至消除掉Dropout的必要性。
• Early stopping 
     在驗證集上如果連續的多次迭代過程中損失函數不再顯著地降低，那麼應該提前結束訓練，詳細參見NIPS 2015 Tutorial slides，或者參見防止過擬合的一些方法。
• Gradient noise 
     Gradient noise[21]即在每次迭代計算梯度中加上一個高斯分佈N(0,σ2t)的隨機誤差，即 
  gt,i=gt,i+N(0,σ2t)
     高斯誤差的方差需要進行退火： 
  σ2t=η(1+t)γ
     對梯度增加隨機誤差會增加模型的魯棒性，即使初始參數值選擇地不好，並適合對特別深層次的負責的網絡進行訓練。其原因在於增加隨機噪聲會有更多的可能性跳過局部極值點並去尋找一個更好的局部極值點，這種可能性在深層次的網絡中更常見。  

總結

   在上文中，對梯度下降算法的三種框架進行了介紹，並且mini-batch梯度下降是使用最廣泛的。隨後，我們重點介紹了SGD的一些優化方法：Momentum、NAG、Adagrad、Adadelta、RMSprop與Adam，以及一些異步SGD方法。最後，介紹了一些提高SGD性能的其它優化建議，如：訓練集隨機洗牌與課程學習(shuffling and curriculum learning)、batch normalization,、early stopping與Gradient noise。 
   希望這篇文章能給你提供一些關於如何使用不同的梯度優化算法方面的指導。如果還有更多的優化建議或方法還望大家提出來？或者你使用什麼技巧和方法來更好地訓練SGD可以一起交流？Thanks。