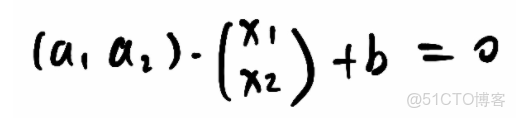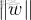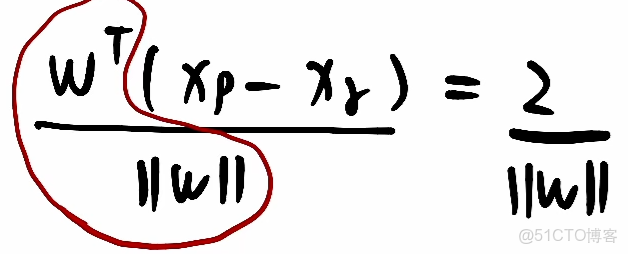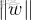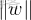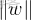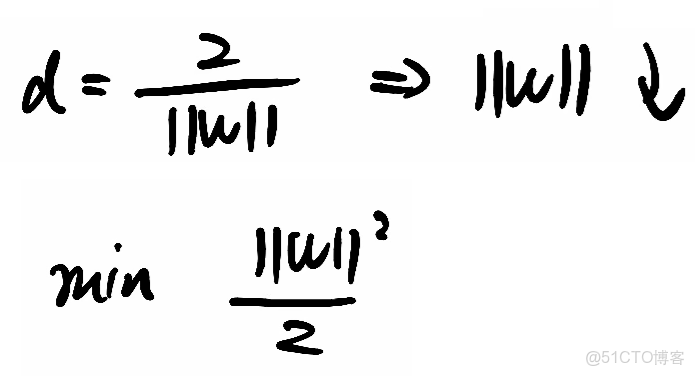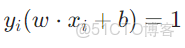目錄
一.SVM的感性認識
1.什麼是 SVM 分類器?
2.核心概念:用通俗例子理解
1. 什麼是 "超平面"?
2. 什麼是 "支持向量"?
3. 為什麼要 "最大間隔"?
3.處理複雜情況
1. 數據分不開怎麼辦?-核函數(非線性問題)
2. 有雜音怎麼辦?(軟間隔)
4.SVM 的優缺點(大白話版)
優點:
缺點:
5.一句話總結
二.正式介紹
1.概念
支持向量與分類超平面示例:
2.什麼是線性分類器?
3.核心思想
三.b站課程算法詳解
1.
2.
3.
四.標準公式化講解
1. 超平面的數學表達
2. 間隔的定義與最大化
(1)距離公式
(2)兩側最近樣本的距離公式
更詳細的解釋為什麼是1和-1?————————————————————————
(3)目標:最大化間隔
3. 支持向量的作用
一.SVM的感性認識
如果你是機器學習零基礎,我們可以用更通俗的方式來理解 SVM 分類器,避免複雜的數學概念。
1.什麼是 SVM 分類器?
SVM(Support Vector Machine,支持向量機)本質上是一種 "找最佳分割線" 的算法,目的是把不同類別的數據分開。
想象一個場景:
- 你有一堆紅蘋果和綠蘋果(兩種數據)
- 你想畫一條線,把紅蘋果和綠蘋果完全分開
- SVM 的作用就是幫你找到這條 "最好" 的線
2.核心概念:用通俗例子理解
1. 什麼是 "超平面"?
- 在二維平面(比如一張紙)上,就是一條直線
- 在三維空間(比如一個盒子)裏,就是一個平面
- 簡單説:用來分隔不同類數據的邊界
2. 什麼是 "支持向量"?
假設你已經畫了一條分隔線:
- 紅蘋果中離這條線最近的那個蘋果
- 綠蘋果中離這條線最近的那個蘋果這兩個蘋果就是 "支持向量",它們決定了這條線的位置。
3. 為什麼要 "最大間隔"?
SVM 的核心是找 "最大間隔" 的線:
- 間隔 = 分隔線到兩邊最近蘋果的距離之和
- 最大間隔的意思是:讓這條線離兩邊最近的蘋果都儘可能遠
為什麼要這樣做?比如有兩條線都能分開紅、綠蘋果:
- 線 A 離紅蘋果很近,離綠蘋果也很近
- 線 B 離兩邊蘋果都很遠顯然線 B 更好,因為如果再來一個稍微靠近邊界的新蘋果,線 B 更不容易分錯(抗干擾能力強)
3.處理複雜情況
1. 數據分不開怎麼辦?-核函數(非線性問題)
有時候紅蘋果和綠蘋果混在一起,比如紅蘋果在中間,綠蘋果在外面圍成一圈,直線肯定分不開。
SVM 的解決辦法:核函數
- 可以理解為 "把數據掰彎" 的工具
- 比如把二維平面的數據 "掰" 成三維的,原本在二維裏繞在一起的點,在三維裏可能就分開了
- 常見的 "掰彎" 方式有:線性(不掰彎)、徑向基(適合大部分複雜情況)、多項式等
2. 有雜音怎麼辦?(軟間隔)
實際數據中常有 "搗蛋鬼":比如一個紅蘋果跑到綠蘋果堆裏了。
SVM 的解決辦法:允許少量錯誤
- 通過參數 C 控制 "嚴格程度"
- C 值大:不允許犯錯,哪怕線歪一點也要把所有蘋果分開(可能過擬合)
- C 值小:允許少數蘋果站錯隊,保證大部分蘋果分得清楚(更穩健)
4.SVM 的優缺點(大白話版)
優點:
- 效果好:尤其是數據維度高(比如文本分類,特徵很多)但樣本不多的時候
- 穩健:不容易被個別異常數據帶偏
- 靈活:能處理直線分不了的複雜數據
缺點:
- 慢:數據太多時,訓練起來費勁
- 挑參數:要試不同的 "掰彎" 方式和嚴格程度,才能找到最佳效果
- 不擅長多分類:原生只能分兩類,要分多類(比如蘋果、香蕉、橘子)需要特殊處理
5.一句話總結
SVM 是一個 "追求完美分割線" 的算法,它找到的線不僅能分開數據,還會盡可能遠離兩邊的數據,遇到複雜情況還能 "掰彎" 空間來處理,適合中小規模、特徵多的分類任務。
如果想動手試試,前面提到的代碼例子可以直接運行,只需要安裝 scikit-learn 庫(pip install scikit-learn),就能直觀看到 SVM 如何工作了。
二.正式介紹
1.概念
SVM(Support Vector Machine,支持向量機),SVM本質模型是特徵空間中最大化間隔的線性分類器,是一種二分類模型。其核心思想是在特徵空間中找到一個最優超平面,將不同類別的樣本分隔開,且使這個超平面與兩側最近樣本(支持向量,支持向量就是離分類超平面(Hyper plane)最近的樣本點)的距離(即 “間隔”)最大化。
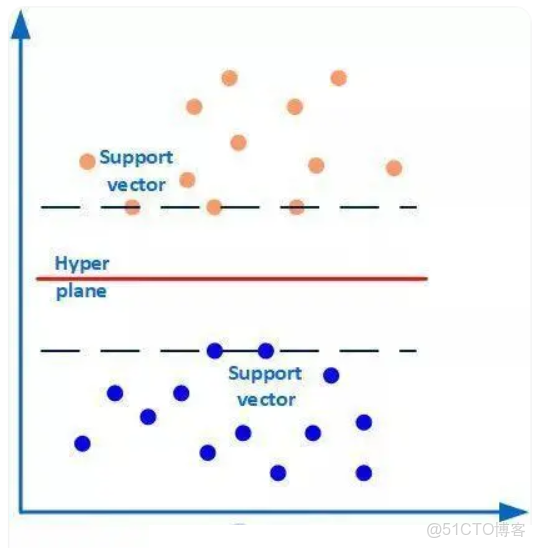
支持向量與分類超平面示例:
如下圖所示,有兩類樣本數據(橙色和藍色的小圓點),中間的紅線是分類超平面,兩條虛線上的點(橙色圓點3個和藍色圓點2個)是距離超平面最近的點,這些點即為支持向量(座標點本身就是向量)。簡單地説,作為支持向量的樣本點非常非常重要,以至於其他的樣本點可以視而不見。而這個分類超平面正是SVM分類器,通過這個分類超平面實現對樣本數據一分為二。
2.什麼是線性分類器?
SVM是一種線性分類器,分類的對象要求是線性可分。因此我們首先要了解什麼是線性可分與線性不可分。
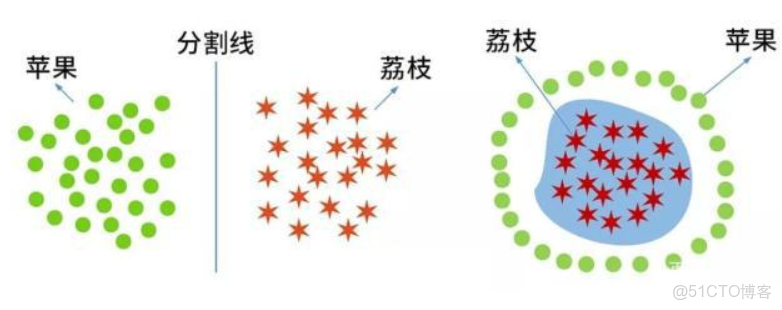
假如在課桌“三八線”的兩旁分別放了一堆蘋果和一堆荔枝,通過“三八線”這樣一條直線就能把蘋果和荔枝這兩種類別的水果分開了(如左下圖),這種情況就是線性可分的。但是如果蘋果和荔枝的放置位置是蘋果包圍荔枝的局面(如右下圖),就無法通過一條直線將它們分開(即這樣的直線是不存在的),這種情況則是線性不可分的情形。當然,這裏舉例的對象是蘋果、荔枝等具體實物。在機器學習上,學習分類的對象則轉化為一系列的樣本特徵數據(比如蘋果、荔枝的相關特徵數據,形狀、顏色等)。
因此,只有當樣本數據是線性可分的,才能找到一條線性分割線或分割面等,SVM分類才能成立。假如樣本特徵數據是線性不可分的,則這樣的線性分割線或分割面是根本不存在的,SVM分類也就無法實現。
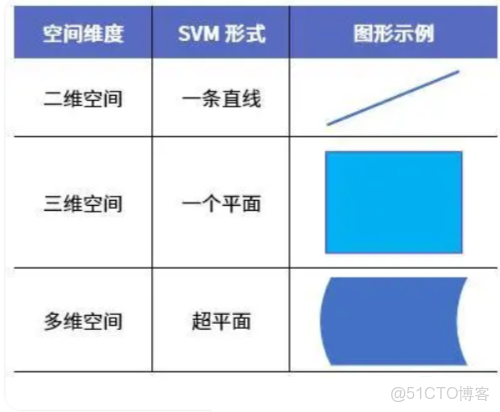
在二維的平面課桌上,一條直線就足以將桌面一分為二。但如果擴展到三維空間中,則需要一個平面(比如一面牆、一扇屏風等)才能將立體空間區域一分為二。而對於高維空間(我們無法用圖畫出),能將其一分為二的則稱為超平面。
對於不同維度空間,SVM的形式特點也不同,具體表現如下:
3.核心思想
SVM的核心是在特徵空間中尋找一個超平面,使得:
- 1.該超平面能將不同類別的樣本“千淨”地分隔開(二分類場景);
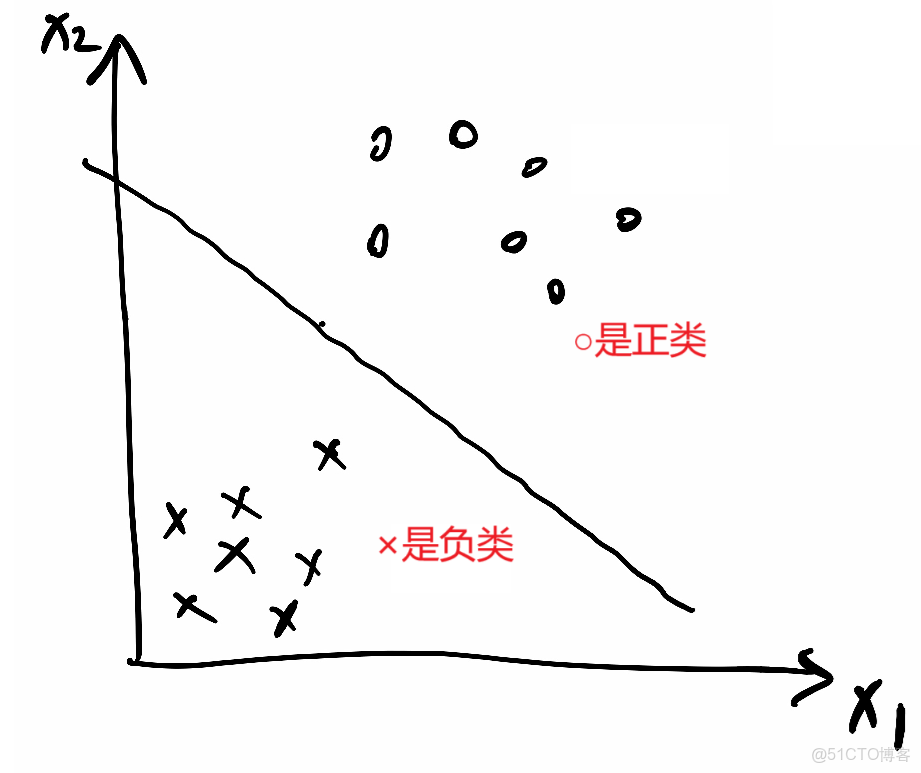
- 2.超平面與兩側最近樣本的距離(即“間隔")最大化。二維空間中,兩類點之間可能有無數條分隔直線,但 “正中間” 那條距離兩側最近點最遠的直線,是最穩健的選擇。
三.b站課程算法詳解
1.
①x和y座標形式寫成x1和x2形式,則分割線公式:a1·x1 + a2·x2 + b = 0
②寫成向量形式:
③又可以寫成 wᵀ·x+b=0 ,w和x就是上面的豎向量
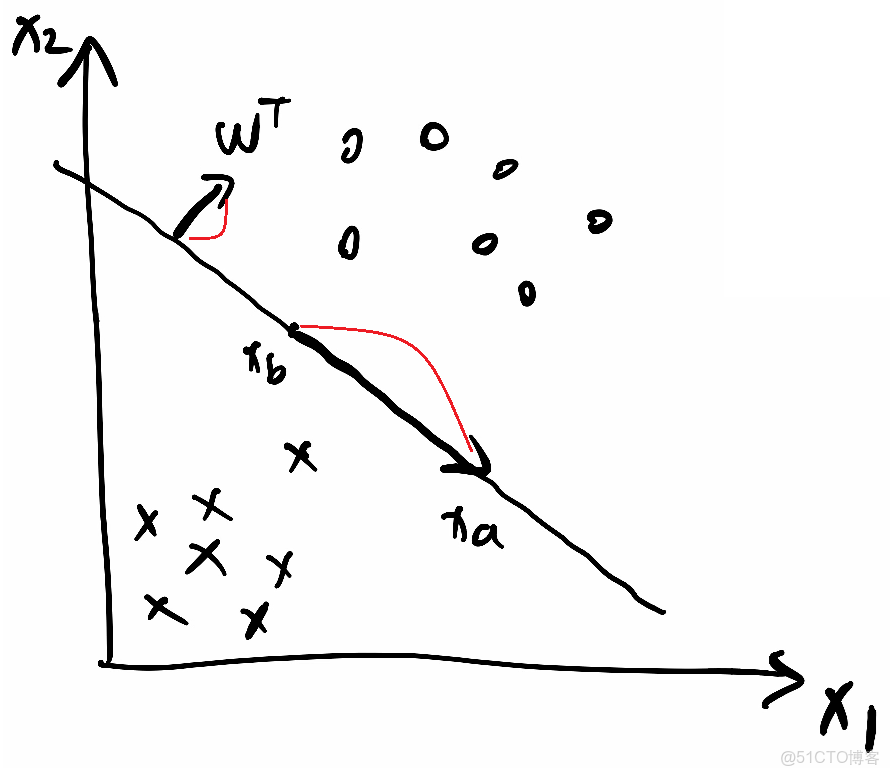
2.
①wᵀ·x+b=0是分割線
②假設分割線上兩個點座標為xa和xb,代入分割線式子,
wᵀ·xa+b=0③
wᵀ·xb+b=0④
③④相減得到wᵀ·(xa-xb)=0⑤
⑤這個式子中xa-xb兩個點相減就是分割線上的一個向量,而點積為0,説明wᵀ與該向量垂直,即説明wᵀ是這個分割線/超平面的法向量
3.
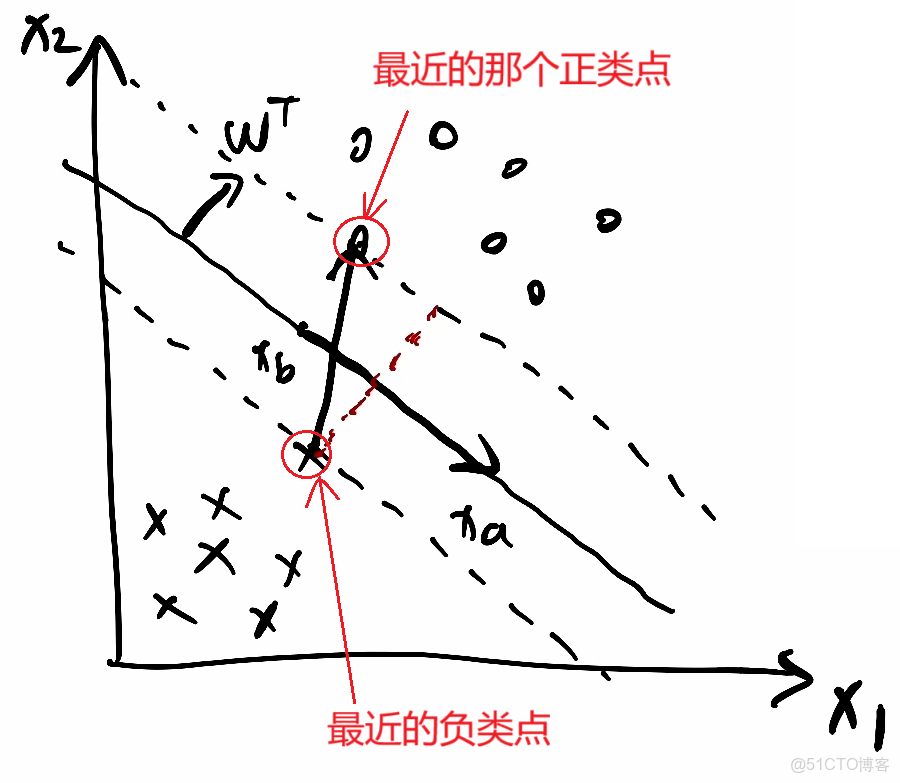
①把分割線向上平移接觸到第一個正樣本點時停下,標上虛線;把分割線向下平移接觸到第一個正樣本點時停下,標上虛線
②假設第一個正樣本點設為xp;第一個負樣本點設為xr,代入
上面的正樣本點虛線方程為:wᵀ·xp+b=k
下面的負樣本點虛線方程為:wᵀ·xr+b=-k
為了簡化計算,我們可以把k除到前面的係數裏面,不影響整體直線方程因此得到兩條簡化的虛線方程:
wᵀ·xp+b=1
wᵀ·xr+b=-1
兩式相減wᵀ·(xp-xr)=2,xp-xr可以看成是從點xr指向xp的一個向量
③此式兩邊同除上
得:
,前面紅圈裏向量除自己的模就是該方向的單位向量,則xp-xr這個向量乘上單位向量,就是在該單位向量上的一個投影,即圖中紅色虛線這個向量。
④該投影就是最大間隔,那他取最大,就得讓
取最小,計算
的最小值,為了便於求導,就去計算1/2 ·
²的最小值,通過拉格朗日對偶性和KKT 條件將問題轉化為更易求解的形式,最終確定超平面參數w和b。
四.標準公式化講解
1. 超平面的數學表達
這裏的+1和-1完全可以替換成任意常數k和-k(解釋在下面的2(2) )
2. 間隔的定義與最大化
間隔(Margin) 指超平面到兩側最近樣本的距離之和。
(1)距離公式
↑上面的這個點到面距離可以類比點到線距離公式推出來↓
(2)兩側最近樣本的距離公式
- w · x + b = 0 是中間的分割線(在三維中就是超平面),而w · x + b ≥ 1 説明在線w · x + b = 1上側的是正類樣本 ,即在分割線w · x + b = 0上側距離該分割線距離大於等於的位置是正類樣本(帶入點到線/點到面的距離公式可得,把上面(1)的di上面帶入w · x + b = 1,計算可得di=)
- w · x + b ≤ 1,意思是在分割線下側距離該分割線距離大於等於的位置是負類樣本。
更詳細的解釋為什麼是1和-1?————————————————————————
這裏的+1和-1完全可以替換成任意常數k和-k,就變成了下面這種形式↓,距離該是多少還是多少,只是係數的樣子看着不一樣了,實際上係數該是幾還是幾,不變,使用+1和-1是為了簡化運算
——————————————————————————————————————————————
(3)目標:最大化間隔
3. 支持向量的作用
滿足
的樣本點稱為支持向量(距離超平面最近的點)。
- 超平面的位置僅由支持向量決定,其他樣本對超平面無影響;
- 模型訓練後,只需保存支持向量即可代表整個模型,減少存儲和計算成本。