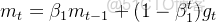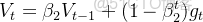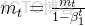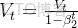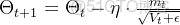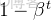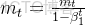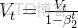一.算法背景
Adam(Adaptive Moment Estimation)是一種廣泛應用於深度學習模型訓練的自適應優化算法,由Diederik P. Kingma和Jimmy Lei Ba於2014年提出,旨在解決傳統優化算法在深度學習中的侷限性。它融合了Momentum動量優化器和RMSProp動態自適應學習率優化器兩種主流優化技術的優勢。
二.數學公式
Adam優化器通過計算梯度的一階矩(均值)和二階矩(方差)來為每個參數自適應地調整學習率。其數學實現步驟如下:
一階矩陣估計(動量項,類似於動量優化器中的動量計算,記錄梯度的指數加權平均值):
二階矩陣估計(自適應學習率項,類似於RMSProp,記錄梯度平方的指數加權平均值):
偏差修正(下面會説為什麼要做這個):
參數更新(和前幾個優化器的更新流程一樣):
代碼實現如下:
import numpy as np
from collections import OrderedDict
import matplotlib.pyplot as plt
class Adam:
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.keys():
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
optimizers= Adam(lr=0.3)
init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0
x_history = []
y_history = []
def f(x, y):
return x**2 / 20.0 + y**2
def df(x, y):
return x / 10.0, 2.0*y
for i in range(30):
x_history.append(params['x'])
y_history.append(params['y'])
grads['x'], grads['y'] = df(params['x'], params['y'])
optimizers.update(params, grads)
x = np.arange(-10, 10, 0.01)
y = np.arange(-5, 5, 0.01)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
# for simple contour line
mask = Z > 7
Z[mask] = 0
idx = 1
# plot
plt.subplot(2, 2, idx)
idx += 1
plt.plot(x_history, y_history, 'o-', color="red")
plt.contour(X, Y, Z)
plt.ylim(-10, 10)
plt.xlim(-10, 10)
plt.plot(0, 0, '+')
# colorbar()
# spring()
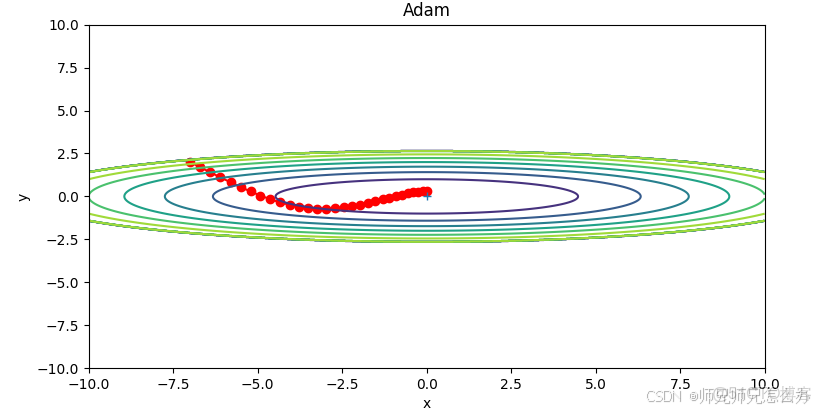
plt.title("Momentum")
plt.xlabel("x")
plt.ylabel("y")
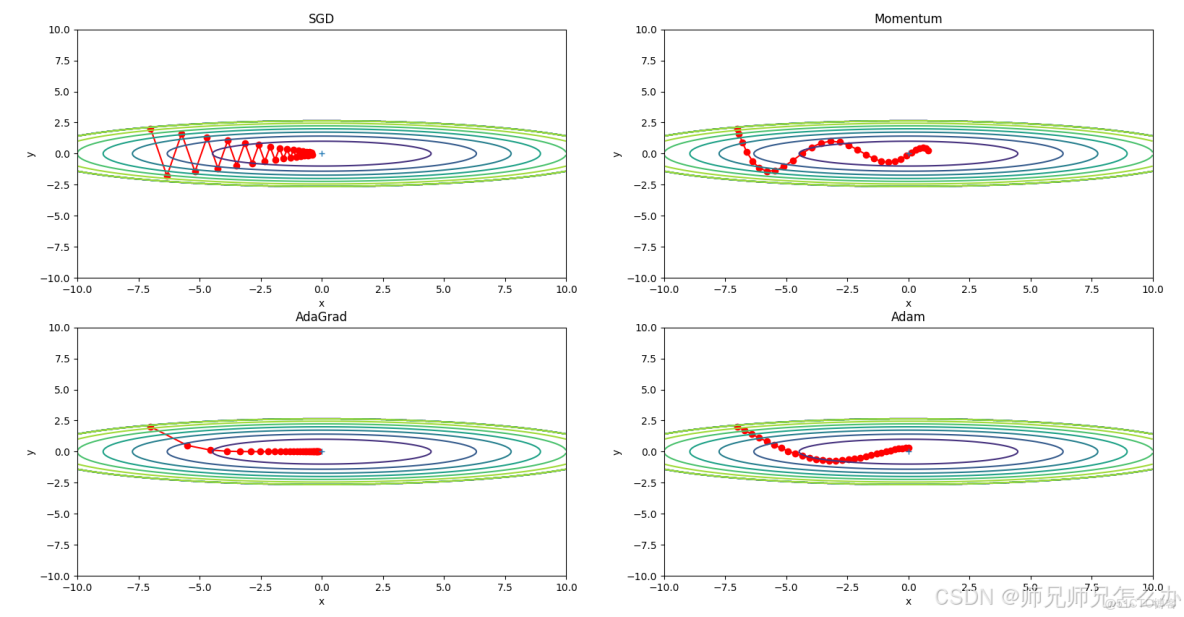
plt.show()運行結果如下:
三.為什麼要進行偏差修正
它解決了指數加權平均在初始階段的估計偏差問題。Adam優化器使用指數加權移動平均(EWMA)來計算梯度的一階矩(m)和二階矩(v)估計。在初始階段,這些估計值會存在系統性偏差,原因在於:
- 初始化問題:m和v通常初始化為0向量,導致初始估計明顯偏低,在t較小時,
- 接近於0,導致未修正的m和v遠小於真實梯度統計量,計算出的學習率會異常偏大。
- 指數加權特性:早期時間步的估計值受初始值影響較大, 修正項隨着t的增加逐漸趨近於1,在訓練後期影響變小,但在初期至關重要。
- 訓練不穩定:參數更新幅度在初期波動劇烈,可能錯過合理的優化方向,增加收斂到次優解的風險,需要更多迭代次數才能克服初始偏差,特別是在稀疏梯度問題上表現更差。
進行偏差修正後,從第一輪迭代就開始積累有意義的梯度統計量,加速模型早期的學習過程,減少對初期學習率的敏感度,使默認參數(β₁=0.9, β₂=0.999)在大多數情況下都能良好工作。
誤差修正通過以下數學公式實現:
其中:
- 和是衰減率(通常取0.9和0.999)
- 是當前時間步(迭代次數)
- 和是未修正的矩估計
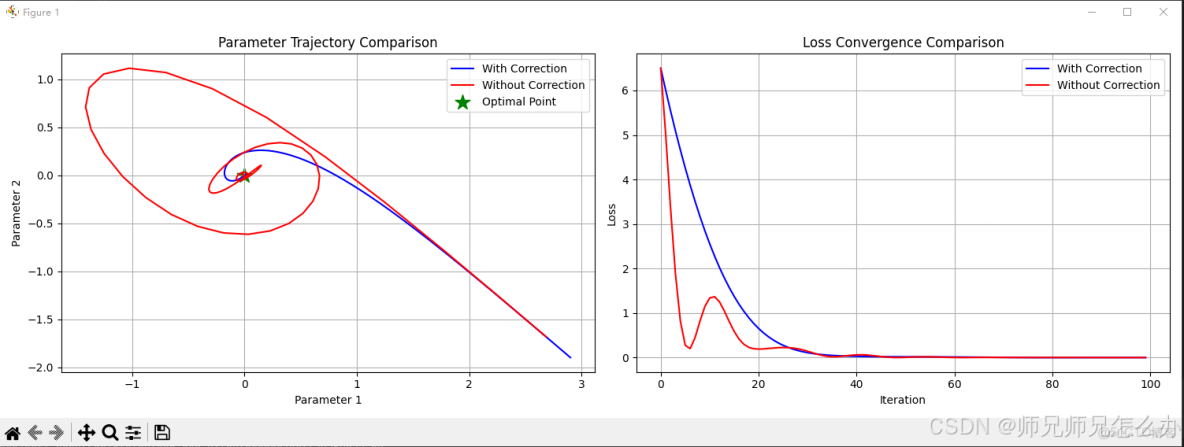
以下使用代碼對不進行偏差修正和進行偏差修正的參數更新軌跡和損失函數收斂的對比:
import numpy as np
import matplotlib.pyplot as plt
class AdamWithCorrection:
"""帶誤差修正的Adam優化器"""
def __init__(self, learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-8):
self.learning_rate = learning_rate
self.beta1 = beta1
self.beta2 = beta2
self.epsilon = epsilon
self.m = None
self.v = None
self.t = 0
self.history = {'params': [], 'loss': []}
def update(self, params, grads, loss):
if self.m is None:
self.m = np.zeros_like(params)
self.v = np.zeros_like(params)
self.t += 1
self.m = self.beta1 * self.m + (1 - self.beta1) * grads
self.v = self.beta2 * self.v + (1 - self.beta2) * (grads ** 2)
# 誤差修正
m_hat = self.m / (1 - self.beta1 ** self.t)
v_hat = self.v / (1 - self.beta2 ** self.t)
params -= self.learning_rate * m_hat / (np.sqrt(v_hat) + self.epsilon)
self.history['params'].append(params.copy())
self.history['loss'].append(loss)
return params
class AdamWithoutCorrection:
"""不帶誤差修正的Adam優化器"""
def __init__(self, learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-8):
self.learning_rate = learning_rate
self.beta1 = beta1
self.beta2 = beta2
self.epsilon = epsilon
self.m = None
self.v = None
self.t = 0
self.history = {'params': [], 'loss': []}
def update(self, params, grads, loss):
if self.m is None:
self.m = np.zeros_like(params)
self.v = np.zeros_like(params)
self.t += 1
self.m = self.beta1 * self.m + (1 - self.beta1) * grads
self.v = self.beta2 * self.v + (1 - self.beta2) * (grads ** 2)
# 無誤差修正
params -= self.learning_rate * self.m / (np.sqrt(self.v) + self.epsilon)
self.history['params'].append(params.copy())
self.history['loss'].append(loss)
return params
# 定義優化問題
def loss_function(x):
return np.sum(0.5 * x**2) # 簡單的二次函數
def gradient_function(x):
return x # 梯度就是x本身
# 初始化參數
params_corr = np.array([3.0, -2.0])
params_no_corr = params_corr.copy()
# 初始化優化器
optimizer_corr = AdamWithCorrection(learning_rate=0.1)
optimizer_no_corr = AdamWithoutCorrection(learning_rate=0.1)
# 優化過程
for i in range(100):
grads_corr = gradient_function(params_corr)
grads_no_corr = gradient_function(params_no_corr)
loss_corr = loss_function(params_corr)
loss_no_corr = loss_function(params_no_corr)
params_corr = optimizer_corr.update(params_corr, grads_corr, loss_corr)
params_no_corr = optimizer_no_corr.update(params_no_corr, grads_no_corr, loss_no_corr)
# 可視化結果
plt.figure(figsize=(15, 5))
# 1. 參數軌跡對比
plt.subplot(1, 2, 1)
params_history_corr = np.array(optimizer_corr.history['params'])
params_history_no_corr = np.array(optimizer_no_corr.history['params'])
plt.plot(params_history_corr[:, 0], params_history_corr[:, 1], label='With Correction', color='blue')
plt.plot(params_history_no_corr[:, 0], params_history_no_corr[:, 1], label='Without Correction', color='red')
plt.scatter([0], [0], color='green', marker='*', s=200, label='Optimal Point')
plt.title('Parameter Trajectory Comparison')
plt.xlabel('Parameter 1')
plt.ylabel('Parameter 2')
plt.legend()
plt.grid(True)
# 2. 損失曲線對比
plt.subplot(1, 2, 2)
plt.plot(optimizer_corr.history['loss'], label='With Correction', color='blue')
plt.plot(optimizer_no_corr.history['loss'], label='Without Correction', color='red')
plt.title('Loss Convergence Comparison')
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()運行代碼可以清晰地看到兩者之間的區別:
四.和其他優化器的對比
與其他優化器的對比:
特點對比:
|
特性
|
Adam
|
SGD
|
Momentum
|
RMSProp
|
|
自適應學習率
|
✓
|
✗
|
✗
|
✓
|
|
動量機制
|
✓
|
✗
|
✓
|
✗
|
|
參數獨立調整
|
✓
|
✗
|
✗
|
✓
|
|
偏差修正
|
✓
|
✗
|
✗
|
✗
|
|
收斂速度
|
快
|
慢
|
中等
|
中等
|
|
超參數數量
|
4
|
1
|
2
|
3
|