文章目錄

• 一、讀題
• 二、算法思路
• 三、代碼實現：

一、讀題

題目來源：https://leetcode.cn/problems/happy-number/description/

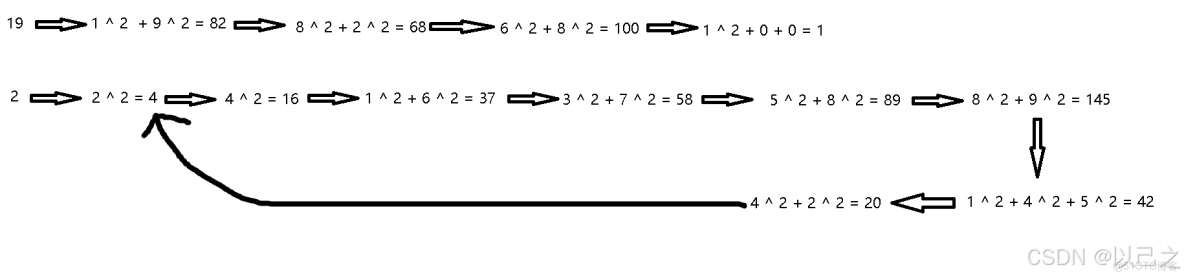
    題目很簡單，把題目給的一個數拆出來，每一位都計算自己的平方，然後相加，一直循環直到平方和為1，當平方和為1的時候循環結束，也有可能不會遇到1一直循環。如果遇到了1就返回true，如果一直遇不到1陷入循環就返回false；

二、算法思路

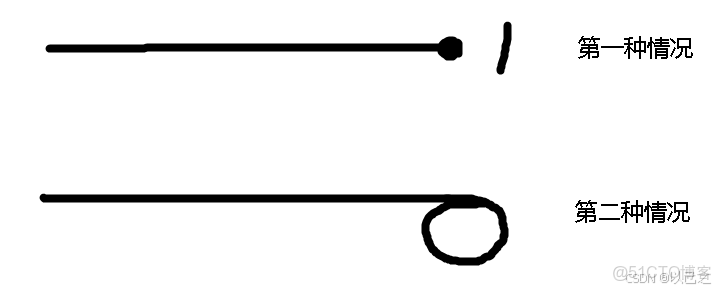
     我們查看題目，結果只會有兩種情況，一種是遇到1不進入循環，一種是進入循環出不來了

     但是我們仔細想，第一種情況真的不進入循環嗎？不不不實際上兩個情況都是循環，1的平方和是1，因此看起來像是沒有進入循環，但是實際上是和第二種情況一樣的，進入循環內出不來了。那麼就很簡單了，我們只需要判斷環內的元素是否為1 即可。

     那既然理解了這種情況，那麼解題思路就很簡單了，不知道大家有沒有做過一道題，就是學習集合的時候的一道算法題，判斷鏈表是否有環，和這道題非常相似，這一道題是已知有環，判斷環內的元素是否是1，我們只需要進入到環內了只會就判斷環內元素是否是1即可。

     這一道題主包的思路是使用雙指針。大家不要被這個名字侷限了，一定要數組下標或者是某一個真正的指針才可以使用這個算法，雙指針只是一個思想，那這一道題來説，如果是判斷鏈表是否有環就可以將指針設置為鏈表的節點，那麼這一道題就需要一個數據結構來配和使用指針來解題嗎？不是的，我們前面説過不要被雙指針這個名字侷限到了，我們可以直接用這個平方和作為指針，而指針的下一個指針就是當前指針的各位平方和。

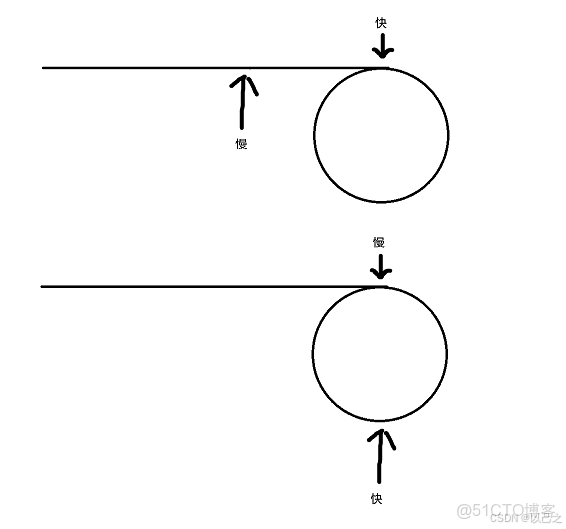
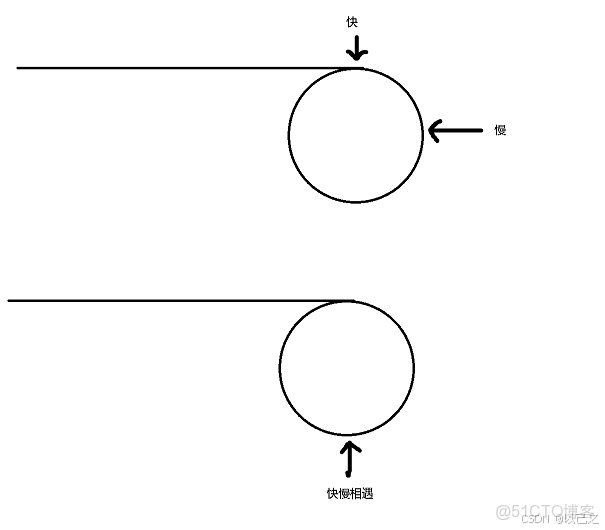
     那麼我們只需要定義兩個指針（快慢指針），一個指針走一步，另一個指針走兩步，那麼當進入環後，兩個指針一定會遇見彼此，當遇到的時候（其實就是兩者相同的時候）判斷該指針數是否是1即可。

     （因為快慢指針一個速度快，一個速度慢，兩倍速度的關係，當路程相同的情況下，一個指針到達終點那麼另一個指針就一定是到達中點也就是一半的路程，當兩個指針都進入環後，兩個指針在相同的圓圈內往下走，慢指針永遠比快指針少走一半的路程，那麼就變成了高中物理的追及相遇問題，快指針走二分之一的路程，那麼慢指針就走四分之一的路程，當快指針已經走完一圈的時候慢指針走一半，這個時候快指針再走二分之一，慢指針到四分之三，那麼兩者的距離越來越近，最終一定會相遇的）

三、代碼實現：

class Solution {
    public int function(int n) {
        int ans = 0;
        while(n != 0) {
            int ret = n % 10 ;
            ans += (ret * ret);
            n /= 10;
        }
        return ans;
    }

    public boolean isHappy(int n) {
        int i = n;
        int j = function(n);
        while(i != j) {
            i = function(i);
            j = function(function(j));
            if(i == j) break;
        }
        return i == 1;
    }
}

    各位佬，如果有什麼更加高效的算法歡迎評論區討論，指導一下主包進步，大家一起共勉